- Noncentral t-distribution
-
Noncentral Student's t Probability density function
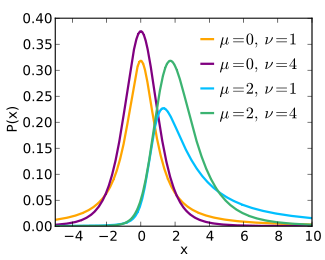
parameters:  degrees of freedom
degrees of freedom
 noncentrality parameter
noncentrality parametersupport: 
pdf: see text cdf: see text mean: see text mode: see text variance: see text skewness: see text ex.kurtosis: see text In probability and statistics, the noncentral t-distribution (also known as the singly noncentral t-distribution) generalizes Student's t-distribution using a noncentrality parameter. Like the central t-distribution, the noncentral t-distribution is primarily used in statistical inference, although it may also be used in robust modeling for data. In particular, the noncentral t-distribution arises in power analysis.
Contents
Characterization
If Z is a normally distributed random variable with unit variance and zero mean, and V is a Chi-squared distributed random variable with
 degrees of freedom that is statistically independent of Z, then
degrees of freedom that is statistically independent of Z, thenis a noncentral t-distributed random variable with
 degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter  . Note that the noncentrality parameter may be negative.
. Note that the noncentrality parameter may be negative.Cumulative distribution function
The cumulative distribution function of noncentral t-distribution with
 degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter  can be expressed as [1]
can be expressed as [1]where
and
 is the cumulative distribution function of the standard normal distribution.
is the cumulative distribution function of the standard normal distribution.
Alternatively, the noncentral t-distribution CDF can be expressed as:
where Γ is the gamma function and I is the regularized incomplete beta function.
Although there are other forms of the cumulative distribution function, the first form presented above is very easy to evaluate through recursive computing.[1] In statistical software R, the cumulative distribution function is implemented as pt.
Probability density function
The probability density function for the noncentral t-distribution with
 degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter  can be expressed in several forms.
can be expressed in several forms.The confluent hypergeometric function form of the density function is
where
 is a confluent hypergeometric function.
is a confluent hypergeometric function.An alternative integral form is [2]
A third form of the density is obtained using its cumulative distribution functions, as follows.
This is the approach implemented by the dt function in R.
Properties
Moments of the Noncentral t-distribution
In general, the kth raw moment of the non-central t-distribution is [3]
In particular, the mean and variance of the noncentral t-distribution are
and
Asymmetry
The noncentral t-distribution is asymmetric unless μ is zero, i.e., a central t-distribution. The right tail will be heavier than the left when μ > 0, and vice versa. However, the usual skewness is not generally a good measure of asymmetry for this distribution, because if the degrees of freedom is not larger than 3, the third moment does not exist at all. Even if the degrees of freedom is greater than 3, the sample estimate of the skewness is still very unstable unless the sample size is very large.
Mode
The noncentral t-distribution is always unimodal and bell shaped, but the mode is not analytically available, although it always lies in the interval[4]
-
-
-
 when
when  and
and when
when 
-
-
Moreover, the mode always has the same sign as the noncentrality parameter
 and the negative of the mode is exactly the mode for a noncentral t-distribution with the same number of degrees of freedom
and the negative of the mode is exactly the mode for a noncentral t-distribution with the same number of degrees of freedom  but noncentrality parameter
but noncentrality parameter 
The mode is strictly increasing with
 when
when  and strictly decreasing with
and strictly decreasing with  when
when  In the limit, when
In the limit, when  approaches zero, the mode is approximated by
approaches zero, the mode is approximated byand when
 approaches infinity, the mode is approximated by
approaches infinity, the mode is approximated byOccurrences
Use in power analysis
Suppose we have an independent and identically distributed sample
 , each of which is normally distributed with mean
, each of which is normally distributed with mean  and variance
and variance  , and we are interested in testing the null hypothesis
, and we are interested in testing the null hypothesis  vs. the alternative hypothesis
vs. the alternative hypothesis  . We can perform a one sample t-test using the test statistic
. We can perform a one sample t-test using the test statisticwhere
 is the sample mean and
is the sample mean and  is the unbiased sample variance. Since the right hand side of the second equality exactly matches the characterization of a noncentral t-distribution as described above,
is the unbiased sample variance. Since the right hand side of the second equality exactly matches the characterization of a noncentral t-distribution as described above,  has a noncentral t-distribution with n − 1 degrees of freedom and noncentrality parameter
has a noncentral t-distribution with n − 1 degrees of freedom and noncentrality parameter  .
.If the test procedure rejects the null hypothesis whenever
 , where
, where  is the upper
is the upper  quantile of the (central) Student's t-distribution for a pre-specified
quantile of the (central) Student's t-distribution for a pre-specified  , then the power of this test is given by
, then the power of this test is given bySimilar applications of the noncentral t-distribution can be found in the power analysis of the general normal-theory linear models, which includes the above one sample t-test as a special case.
Related distributions
- Central t distribution: The central t-distribution can be converted into a location/scale family. This family of distributions is used in data modeling to capture various tail behaviors. The location/scale generalization of the central t-distribution is a different distribution from the noncentral t-distribution discussed in this article. In particular, this approximation does not respect the asymmetry of the noncentral t-distribution. However, the central t-distribution can be used as an approximation to the non-central t-distribution.[5]
- If
 is noncentral t-distributed with
is noncentral t-distributed with  degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter  and
and  , then
, then  has a noncentral F-distribution with 1 numerator degree of freedom,
has a noncentral F-distribution with 1 numerator degree of freedom,  denominator degrees of freedom, and noncentrality parameter
denominator degrees of freedom, and noncentrality parameter  .
.
- If
 is noncentral t-distributed with
is noncentral t-distributed with  degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter  and
and  , then
, then  has a normal distribution with mean
has a normal distribution with mean  and unit variance.
and unit variance.
- When the denominator noncentrality parameter of a edit] Special cases
- When
 , the noncentral t-distribution becomes the central (Student's) t-distribution with the same degrees of freedom.
, the noncentral t-distribution becomes the central (Student's) t-distribution with the same degrees of freedom.
See also
References
- ^ a b Lenth, Russell V (1989). "Algorithm AS 243: Cumulative Distribution Function of the Non-central t Distribution". Journal of the Royal Statistical Society. Series C (Applied Statistics) 38: 185–189. JSTOR 2347693.
- ^ L. Scharf, Statistical Signal Processing, (Massachusetts: Addison-Wesley, 1991), p.177.
- ^ Hogben, D; Wilk, MB (1961). "The moments of the non-central t-distribution". Biometrika 48: 465–468. JSTOR 2332772.
- ^ van Aubel, A; Gawronski, W (2003). "Analytic properties of noncentral distributions". Applied Mathematics and Computation 141: 3–12. doi:10.1016/S0096-3003(02)00316-8. http://www.sciencedirect.com/science/article/B6TY8-47G44WX-V/2/7705d2642b1a384b13e0578898a22d48.
- ^ Helena Chmura Kraemer; Minja Paik (1979). "A Central t Approximation to the Noncentral t Distribution". Technometrics 21 (3): 357–360. JSTOR 1267759.
External links
- Eric W. Weisstein. "Noncentral Student's t-Distribution." From MathWorld—A Wolfram Web Resource
Some common univariate probability distributions Continuous beta • Cauchy • chi-squared • exponential • F • gamma • Laplace • log-normal • normal • Pareto • Student's t • uniform • WeibullDiscrete List of probability distributions Statistics Descriptive statistics Summary tablesPearson product-moment correlation · Rank correlation (Spearman's rho, Kendall's tau) · Partial correlation · Scatter plotBar chart · Biplot · Box plot · Control chart · Correlogram · Forest plot · Histogram · Q-Q plot · Run chart · Scatter plot · Stemplot · Radar chartData collection Designing studiesDesign of experiments · Factorial experiment · Randomized experiment · Random assignment · Replication · Blocking · Optimal designUncontrolled studiesStatistical inference Frequentist inferenceSpecific testsZ-test (normal) · Student's t-test · F-test · Pearson's chi-squared test · Wald test · Mann–Whitney U · Shapiro–Wilk · Signed-rank · Kolmogorov–Smirnov testCorrelation and regression analysis Errors and residuals · Regression model validation · Mixed effects models · Simultaneous equations modelsNon-standard predictorsPartition of varianceCategorical, multivariate, time-series, or survival analysis Decomposition (Trend · Stationary process) · ARMA model · ARIMA model · Vector autoregression · Spectral density estimationApplications Category · Portal · Outline · Index - When
Categories:- Continuous distributions
Wikimedia Foundation. 2010.



![\tilde{F}_{\nu,\mu}(x)=
\Phi(-\mu)+\frac{1}{2}\sum_{j=0}^\infty\left[p_jI_y\left(j+\frac{1}{2},\frac{\nu}{2}\right)+q_jI_y\left(j+1,\frac{\nu}{2}\right)\right],](7/157e51f5fa96d3272cd2216ae8099e69.png)
 is the
is the 






![f(x)=
\begin{cases}\frac{\nu}{x} \left[F_{\nu+2,\mu}(x\sqrt{1+2/\nu}) - F_{\nu,\mu}(x)\right],
&\mbox{if } x\neq 0 ; \\
\frac{ \Gamma(\,(\nu+1)/2\,)}{\sqrt{\pi\nu} \Gamma(\nu/2)}
\exp\left\{-{\mu^2}/{2}\right\},
&\mbox{if } x=0.
\end{cases}](0/f709336fa0a74865e45078d103f2074f.png)
![\mbox{E}\left[T^k\right]=
\begin{cases}
\left(\frac{\nu}{2}\right)^{\frac{k}{2}}\frac{\Gamma\left(\frac{\nu-k}{2}\right)}{\Gamma\left(\frac{\nu}{2}\right)}\mbox{exp}\left(-\frac{\mu^2}{2}\right)\frac{d^k}{d \mu^k}\mbox{exp}\left(\frac{\mu^2}{2}\right),
& \mbox{if }\nu>k ; \\
\mbox{Does not exist} ,
& \mbox{if }\nu\le k .\\
\end{cases}](2/b628ea03c2310b3742fc141d4936b3b1.png)
![\mbox{E}\left[T\right]=
\begin{cases}
\mu\sqrt{\frac{\nu}{2}}\frac{\Gamma((\nu-1)/2)}{\Gamma(\nu/2)},
&\mbox{if }\nu>1 ;\\
\mbox{Does not exist},
&\mbox{if }\nu\le1 ,\\
\end{cases}](1/561664a2be666be0bc1547d7e3bed88b.png)
![\mbox{Var}\left[T\right]=
\begin{cases}
\frac{\nu(1+\mu^2)}{\nu-2}
-\frac{\mu^2\nu}{2}
\left(\frac{\Gamma((\nu-1)/2)}{\Gamma(\nu/2)}\right)^2 ,
&\mbox{if }\nu>2 ;\\
\mbox{Does not exist},
&\mbox{if }\nu\le2 .\\
\end{cases}](4/d04e8bbb52ced7172435e383fa7c84c0.png)



