Wallenius' noncentral hypergeometric distribution

Introduction

---

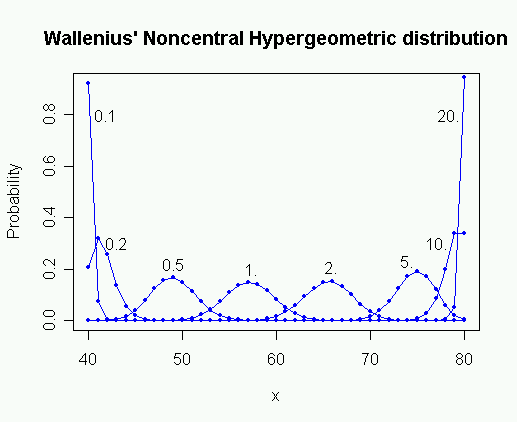
right|thumb|300px">
Probability mass function for Wallenius' Noncentral Hypergeometric Distribution for different values of the odds ratio ω.
m₁ = 80, m₂ = 60, n = 100, ω = 0.1 ... 20

In probability theory and statistics, Wallenius' noncentral hypergeometric distribution is a generalization of the hypergeometric distribution where items are sampled with bias.

This distribution can be illustrated as an urn model with bias. Assume, for example, that an urn contains "m"₁ red balls and "m"₂ white balls, totalling "N" = "m"₁ + "m"₂ balls. Each red ball has the weight ω₁ and each white ball has the weight ω₂. We will say that the odds ratio is ω = ω₁ / ω₂. Now we are taking "n" balls, one by one, in such a way that the probability of taking a particular ball at a particular draw is equal to its proportion of the total weight of all balls that lie in the urn at that moment. The number of red balls "x"₁ that we get in this experiment is a random variable with Wallenius' noncentral hypergeometric distribution.

The matter is complicated by the fact that there is more than one noncentral hypergeometric distribution. Wallenius' noncentral hypergeometric distribution is obtained if balls are sampled one by one in such a way that there is competition between the balls. Fisher's noncentral hypergeometric distribution is obtained if the balls are sampled simultaneously or independently of each other. Unfortunately, both distributions are known in the literature as "the" noncentral hypergeometric distribution. It is important to be specific about which distribution is meant when using this name.

The two distributions are both equal to the (central) hypergeometric distribution when the odds ratio is 1.

It is far from obvious why these two distributions are different. See the Wikipedia entry on noncentral hypergeometric distributions for a more detailed explanation of the difference between these two probability distributions.

Univariate distribution

Probability distribution
name =Univariate Wallenius' Noncentral Hypergeometric Distribution
type =mass
pdf_

cdf_

parameters =$m\_1,\; m\_2\; in\; mathbb\{N\}$
$N\; =\; m\_1\; +\; m\_2$
$n\; in\; [0,N)$
$omega\; in\; mathbb\{R\}\_+$
support =$x\; in\; [x\_\{min\},x\_\{max\}]$
$x\_\{min\}=max(0,n-m\_2)$
$x\_\{max\}=min(n,m\_1)$
pdf =
where $D=omega(m\_1-x\_1)+(m\_2-x\_2)$
cdf =
mean =Approximated by solution $mu$ to
$frac\{mu\}\{m\_1\}\; +\; left(1-frac\{n-mu\}\{m\_2\}\; ight)^\{omega\}\; =\; 1$
median =
mode =
variance =$approx\; frac\{Nab\}\{(N-1)(m\_1\; b\; +\; m\_2\; a)\},$, where
$a=mu(m\_1-mu),;\; b=(n-mu)(mu+m\_2-n)$
skewness =
kurtosis =
entropy =
mgf =
char =

Wallenius' distribution is particularly complicated because each ball has a probability of being taken that depends not only on its weight, but also on the total weight of its competitors. And the weight of the competing balls depends on the outcomes of all preceding draws.

This recursive dependency gives rise to a difference equation with a solution that is given in open form by the integral in the expression of the probability mass function in the table above.

Closed form expressions for the probability mass function exist (Lyons, 1980), but they are not very useful for practical calculations because of extreme numerical instability, except in degenerate cases.

Several other calculation methods are used, including recursion, Taylor expansion and numerical integration (Fog, 2007, 2008).

The most reliable calculation method is recursive calculation of f("x","n") from f("x","n"-1) and f("x"-1,"n"-1) using the recursion formula given below under properties. The probabilities of all ("x","n") combinations on all possible trajectories leading to the desired point are calculated, starting with f(0,0) = 1 as shown on the figure to the right. The total number of probabilities to calculate is "n"("x"+1)-"x"². Other calculation methods must be used when "n" and "x" are so big that this method is too inefficient.

The probability that all balls have the same color is easier to calculate. See the formula below under multivariate distribution.

No exact formula for the mean is known (short of complete enumeration of all probabilities). The equation given above is reasonably accurate. This equation can be solved for μ by Newton-Raphson iteration. The same equation can be used for estimating the odds from an experimentally obtained value of the mean.

Multivariate distribution

The distribution can be expanded to any number of colors "c" of balls in the urn. The multivariate distribution is used when there are more than two colors.

Probability distribution
name =Multivariate Wallenius' Noncentral Hypergeometric Distribution
type =mass
pdf_

cdf_

parameters =$c\; in\; mathbb\{N\}$
$mathbf\{m\}=(m\_1,ldots,m\_c)\; in\; mathbb\{N\}^c$
$N\; =\; sum\_\{i=1\}^c\; m\_i$
$n\; in\; [0,N)$

support =$mathrm\{S\}\; =\; left\{\; mathbf\{x\}\; in\; mathbb\{Z\}\_\{0+\}^c\; ,\; :\; ,\; sum\_\{i=1\}^\{c\}\; x\_i\; =\; n\; ight\}$
pdf =
where
cdf =
mean =Approximated by solution $mu\_1,ldots,mu\_c$ to
$left(1-frac\{mu\_1\}\{m\_1\}\; ight)^\{1/omega\_1\}\; =\; left(1-frac\{mu\_2\}\{m\_2\}\; ight)^\{1/omega\_2\}\; =\; ldots\; =\; left(1-frac\{mu\_c\}\{m\_c\}\; ight)^\{1/omega\_c\}$
$wedge\; ,\; sum\_\{i=1\}^c\; mu\_i\; =\; n\; ,\; wedge\; ,\; forall,\; i\; in\; [0,c]\; ,\; :,\; 0\; le\; mu\_i\; le\; m\_i,.$
median =
mode =
variance =Approximated by variance of Fisher's noncentral hypergeometric distribution with same mean.
skewness =
kurtosis =
entropy =
mgf =
char =

The probability mass function can be calculated by various Taylor expansion methods or by numerical integration (Fog, 2008).

The probability that all balls have the same color, "j", can be calculated as::for "x"_j = "n" ≤ "m"_j, where the underlined superscript denotes the falling factorial as defined above.

A reasonably good approximation to the mean can be calculated using the equation given above. The equation can be solved by defining θ so that:$mu\_i\; =\; m\_i(1-e^\{omega\_i\; heta\})$and solving:$sum\_\{i=1\}^c\; mu\_i\; =\; n$for θ by Newton-Raphson iteration.

The equation for the mean is also useful for estimating the odds from experimentally obtained values for the mean.

No good way of calculating the variance is known. The best known method is to approximate the multivariate Wallenius distribution by a multivariate Fisher's noncentral hypergeometric distribution with the same mean, and insert the mean as calculated above in the approximate formula for the variance of the latter distribution.

Properties

The order of the colors is arbitrary so that any colors can be swapped.

The weights can be arbitrarily scaled:: for all $r\; in\; mathbb\{R\}\_+$.

Colors with zero number ("m"_i = 0) or zero weight (ω_i = 0) can be omitted from the equations.

Colors with the same weight can be joined::$operatorname\{mwnchypg\}left(mathbf\{x\};n,mathbf\{m\},\; (omega\_1,ldots,omega\_\{c-1\},omega\_\{c-1\})\; ight),\; =$::$operatorname\{mwnchypg\}left((x\_1,ldots,x\_\{c-1\}+x\_c);\; n,(m\_1,ldots,m\_\{c-1\}+m\_c),\; (omega\_1,ldots,omega\_\{c-1\})\; ight),\; cdot$::$operatorname\{hypg\}(x\_c;\; x\_\{c-1\}+x\_c,\; m\_c,\; m\_\{c-1\}+m\_c),,$where $operatorname\{hypg\}(x;n,m,N)$ is the (univariate, central) hypergeometric distribution probability.

Complementary Wallenius' noncentral hypergeometric distribution

---

right|thumb|300px">
Probability mass function for the Complementary Wallenius' Noncentral Hypergeometric Distribution for different values of the odds ratio ω.
m₁ = 80, m₂ = 60, n = 40, ω = 0.05 ... 10

The balls that are "not" taken in the urn experiment have a distribution that is different from Wallenius' noncentral hypergeometric distribution, due to a lack of symmetry. The distribution of the balls not taken can be called the complementary Wallenius' noncentral hypergeometric distribution.

Probabilities in the complementary distribution are calculated from Wallenius' distribution by replacing "n" with "N"-"n", "x"_i with "m"_i - "x"_i, and ω_i with 1/ω_i.

oftware available

* An implementation for the R programming language is available as the package named [http://cran.stat.ucla.edu/src/contrib/Descriptions/BiasedUrn.html BiasedUrn] . Includes univariate and multivariate probability mass functions, distribution functions, quantiles, random variable generating functions, mean and variance.
* Implementation in C++ is available from [http://www.agner.org/random/ www.agner.org] .

ee also

* Noncentral hypergeometric distributions
* Fisher's noncentral hypergeometric distribution
* Hypergeometric distribution
* Urn models
* Biased sample
* Bias
* Population genetics
* Fisher's exact test

References

Citation
last=Chesson
first=J.
year=1976
title=A non-central multivariate hypergeometric distribution arising from biased sampling with application to selective predation
periodical=Journal of Applied Probability
volume=13
pages=795-797.

Citation
last=Fog
first=A.
year=2007
title=Random number theory
url=http://www.agner.org/random/theory/.

Citation
last=Fog
first=A.
year=2008
title=Calculation Methods for Wallenius' Noncentral Hypergeometric Distribution
periodical=Communications In statictics, Simulation and Computation
volume=37
issue=2
pages=258-273.

Citation
last=Johnson
first=N. L.
last2=Kemp
first2=A. W.
last3=Kotz
first3=S.
author-link=
year=2005
title=Univariate Discrete Distributions
publisher=Wiley and Sons
place=Hoboken, New Jersey.

Citation
last=Lyons
first=N. I.
year=1980
title=Closed Expressions for Noncentral Hypergeometric Probabilities
periodical=Communications In statictics, B
volume=9
pages=313-314.

Citation
last=Manly
first=B. F. J.
year=1974
title=A Model for Certain Types of Selection Experiments
periodical=Biometrics
volume=30
pages=281-294.

Citation
last=Wallenius
first=K. T.
year=1963
title=Biased Sampling: The Non-central Hypergeometric Probability Distribution. Ph.D. Thesis
publisher=Stanford University, Department of Statistics.