Failure rate

Failure rate is the frequency with which an engineered system or component fails, expressed for example in failures per hour. It is often denoted by the Greek letter λ (lambda) and is important in reliability engineering.

The failure rate of a system usually depends on time, with the rate varying over the life cycle of the system. For example, an automobile's failure rate in its fifth year of service may be many times greater than its failure rate during its first year of service. One does not expect to replace an exhaust pipe, overhaul the brakes, or have major transmission problems in a new vehicle.

In practice, the mean time between failures (MTBF, 1/λ) is often used instead of the failure rate. This is valid if the failure rate is constant (general agreement in some reliability standards (Military and Aerospace) - part of the flat region of the bathtub curve , also called the "useful life period". The MTBF is an important system parameter in systems where failure rate needs to be managed, in particular for safety systems. The MTBF appears frequently in the engineering design requirements, and governs frequency of required system maintenance and inspections. In special processes called renewal processes, where the time to recover from failure can be neglected and the likelihood of failure remains constant with respect to time, the failure rate is simply the multiplicative inverse of the MTBF (1/λ).

A similar ratio used in the transport industries, especially in railways and trucking is 'mean distance between failures', a variation which attempts to correlate actual loaded distances to similar reliability needs and practices.

Failure rates are important factors in the insurance, finance, commerce and regulatory industries and fundamental to the design of safe systems in a wide variety of applications.

Failure rate in the discrete sense

The failure rate can be defined as the following:

The total number of failures within an item population, divided by the total time expended by that population, during a particular measurement interval under stated conditions. (MacDiarmid, et al.)

Although the failure rate, λ(t), is often thought of as the probability that a failure occurs in a specified interval given no failure before time t, it is not actually a probability because it can exceed 1. Erroneous expression of the failure rate in % could result in incorrect perception of the measure, specially if it would be measured from repairable systems and multiple systems with non-constant failure rates or different operation times. It can be defined with the aid of the reliability function or survival function R(t), the probability of no failure before time t.

Failure_rate(t)= f(t)/R(t), where f(t) is the time to (first) failure distribution and R(t) is 1 - F(t):

$\lambda = \frac{R(t_1)-R(t_2)}{(t_2-t_1) \cdot R(t_1)} = \frac{R(t)-R(t+\triangle t)}{\triangle t \cdot R(t)} \!$

over a time interval (t₂ − t₁) from t₁ (or t) to t₂ and Δt is defined as (t₂ − t₁). Note that this is a conditional probability, hence the R(t) in the denominator.

The failure_rate (t) function is a CONDITIONAL probability of failure DENSITY function. The condition is that the failure has not occurred at time t.

Hazard rate and ROCOF (rate of occurrence of failures) is often incorrectly seen as the same and equal to the failure rate. And literature is even contaminated with inconsistent definitions. The hazard rate is in contrast to the ROCOF the same a failure rate. ROCOF is used for repairable systems only. In practice not many serious errors are made due to this confusion (although this statement is hard to validate...).

Failure rate in the continuous sense

Exponential failure density functions

Calculating the failure rate for ever smaller intervals of time, results in the hazard function (or hazard rate), h(t). This becomes the instantaneous failure rate as $\scriptstyle\Delta t$ tends to zero:

$h(t)=\lim_{\triangle t \to 0} \frac{R(t)-R(t+\triangle t)}{\triangle t \cdot R(t)}.$

A continuous failure rate depends on the existence of a failure distribution, $\scriptstyle F(t)$, which is a cumulative distribution function that describes the probability of failure (at least) up to and including time t,

$\operatorname{Pr}(T\le t)=F(t)=1-R(t),\quad t\ge 0. \!$

where T is the failure time. The failure distribution function is the integral of the failure density function, f(t),

$F(t)=\int_{0}^{t} f(\tau)\, d\tau. \!$

The hazard function can be defined now as

$h(t)=\frac{f(t)}{R(t)}. \!$

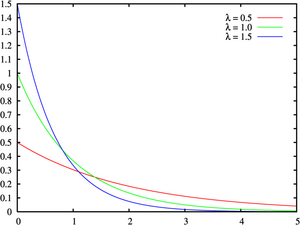
Many probability distributions can be used to model the failure distribution (see List of important probability distributions). A common model is the exponential failure distribution,

$F(t)=\int_{0}^{t} \lambda e^{-\lambda \tau}\, d\tau = 1 - e^{-\lambda t}, \!$

which is based on the exponential density function. The hazard rate function for this is:

$h(t) = \frac{f(t)}{R(t)} = \frac{\lambda e^{-\lambda t}}{e^{-\lambda t}} = \lambda .$

Thus, for an exponential failure distribution, the hazard rate is a constant with respect to time (that is, the distribution is "memory-less"). For other distributions, such as a Weibull distribution or a log-normal distribution, the hazard function may not be constant with respect to time. For some such as the deterministic distribution^{[citation needed]} it is monotonic increasing (analogous to "wearing out"), for others such as the Pareto distribution it is monotonic decreasing (analogous to "burning in"), while for many it is not monotonic.

Failure rate data

Failure rate data can be obtained in several ways. The most common means are:

• Historical data about the device or system under consideration.

Many organizations maintain internal databases of failure information on the devices or systems that they produce, which can be used to calculate failure rates for those devices or systems. For new devices or systems, the historical data for similar devices or systems can serve as a useful estimate.

• Government and commercial failure rate data.

Handbooks of failure rate data for various components are available from government and commercial sources. MIL-HDBK-217F, Reliability Prediction of Electronic Equipment, is a military standard that provides failure rate data for many military electronic components. Several failure rate data sources are available commercially that focus on commercial components, including some non-electronic components.

• Testing.

The most accurate source of data is to test samples of the actual devices or systems in order to generate failure data. This is often prohibitively expensive or impractical, so that the previous data sources are often used instead.

Units

Failure rates can be expressed using any measure of time, but hours is the most common unit in practice. Other units, such as miles, revolutions, etc., can also be used in place of "time" units.

Failure rates are often expressed in engineering notation as failures per million, or 10⁻⁶, especially for individual components, since their failure rates are often very low.

The Failures In Time (FIT) rate of a device is the number of failures that can be expected in one billion (10⁹) device-hours of operation. (E.g. 1000 devices for 1 million hours, or 1 million devices for 1000 hours each, or some other combination.) This term is used particularly by the semiconductor industry.

The relationship of FIT to MTBF may be expressed as: MTBF = 1,000,000,000 x 1/FIT.

Additivity

Under certain engineering assumptions (e.g. besides the above assumptions for a constant failure rate, the assumption that the considered system has no relevant redundancies), the failure rate for a complex system is simply the sum of the individual failure rates of its components, as long as the units are consistent, e.g. failures per million hours. This permits testing of individual components or subsystems, whose failure rates are then added to obtain the total system failure rate.^{[citation needed]}

Example

Suppose it is desired to estimate the failure rate of a certain component. A test can be performed to estimate its failure rate. Ten identical components are each tested until they either fail or reach 1000 hours, at which time the test is terminated for that component. (The level of statistical confidence is not considered in this example.) The results are as follows:

Estimated failure rate is

$\frac{6\text{ failures}}{7502\text{ hours}} = 0.0007998 \frac\text{failures}\text{hour} = 799.8 \times 10^{-6} \frac\text{failures}\text{hour},$

or 799.8 failures for every million hours of operation.

Estimation

The Nelson–Aalen estimator can be used to estimate the cumulative hazard rate function.

See also

Statistics portal

• Annualized failure rate
• Burn in
• Failure mode
• Force of mortality
• Reliability
• Reliability theory
• Reliability theory of aging and longevity
• Survival analysis
• Weibull distribution

References

Print

• Blanchard, Benjamin S. (1992), Logistics Engineering and Management, Fourth Ed., pp 26–32, Prentice-Hall, Inc., Englewood Cliffs, New Jersey.
• Ebeling, Charles E., (1997), An Introduction to Reliability and Maintainability Engineering, pp 23–32, McGraw-Hill Companies, Inc., Boston.
• Federal Standard 1037C
• Kapur, K.C., and Lamberson, L.R., (1977), Reliability in Engineering Design, pp 8–30, John Wiley & Sons, New York.
• Knowles, D.I.,(1995), Should We Move Away From "Acceptable Failure Rate", Communications in Reliability Maintainability and Supportability, Vol. 2, No. 1, P. 23, International RMS Committee, USA
• MacDiarmid, Preston; Morris, Seymour; et al., (no date), Reliability Toolkit: Commercial Practices Edition, pp 35–39, Reliability Analysis Center and Rome Laboratory, Rome, New York.
• Rausand, M. and Hoyland, A., (2004), System Reliability Theory; Models, Statistical methods, and Applications, John Wuiley & Sons, New York. NTNU.no
• Turner, T., Hockley, C., and Burdaky, R., (1997), The Customer Needs A Maintenance-Free Operating Period, 1997 Avionics Conference and Exhibition, No. 97-0819, P. 2.2, ERA Technology Ltd., Leatherhead, Surrey, UK

Online

• Mondro, Mitchell J, (June 2002), "Approximation of Mean Time Between Failure When a System has Periodic Maintenance", IEEE Transactions on Reliability, v 51, no 2. (available from MITRE Corp.)
• Reliability Prediction of Electronic Equipment, MIL-HDBK-217F(2), (DOD download site.)
• Bathtub curve issues by ASQC.
• Fault Tolerant Computing in Industrial Automation by Hubert Kirrmann, ABB Research Center, Switzerland

External links

• Usenet FAQ about MTBF
• Reliability and Availability Basics
• Product failure behavior and wear out