Cluster analysis

The result of a cluster analysis shown as the coloring of the squares into three clusters.

Cluster analysis or clustering is the task of assigning a set of objects into groups (called clusters) so that the objects in the same cluster are more similar (in some sense or another) to each other than to those in other clusters.

Clustering is a main task of explorative data mining, and a common technique for statistical data analysis used in many fields, including machine learning, pattern recognition, image analysis, information retrieval, and bioinformatics.

Cluster analysis itself is not one specific algorithm, but the general task to be solved. It can be achieved by various algorithms that differ significantly in their notion of what constitutes a cluster and how to efficiently find them. Popular notions of clusters include groups with low distances among the cluster members, dense areas of the data space, intervals or particular statistical distributions. The appropriate clustering algorithm and parameter settings (including values such as the distance function to use, a density threshold or the number of expected clusters) depend on the individual data set and intended use of the results. Cluster analysis as such is not an automatic task, but an iterative process of knowledge discovery that involves try and failure. It will often be necessary to modify preprocessing and parameters until the result achieves the desired properties.

Besides the term clustering, there are a number of terms with similar meanings, including automatic classification, numerical taxonomy, botryology (from Greek βότρυς "grape") and typological analysis. The subtle differences are often in the usage of the results: while in data mining, the resulting groups are the matter of interest, in automatic classification primarily their discriminitative power is of interest. This often leads to misunderstandings of researchers coming from the fields of data mining and machine learning, since they use the same terms and often the same algorithms, but have different goals.

Clusters and clusterings

The notion of a cluster varies between algorithms and is one of the many decisions to take when choosing the appropriate algorithm for a particular problem. At first the terminology of a cluster seems obvious: a group of data objects. However, the clusters found by different algorithms vary significantly in their properties, and understanding these cluster models is key to understanding the differences between the various algorithms. Typical cluster models include:

• Connectivity models: for example hierarchical clustering builds models based on distance connectivity.
• Centroid models: for example the k-means algorithm represents each cluster by a single mean vector.
• Distribution models: clusters are modeled using statistic distributions, such as multivariate normal distributions used by the Expectation-maximization algorithm.
• Density models: for example DBSCAN and OPTICS defines clusters as connected dense regions in the data space.
• Subspace models: in Biclustering (also known as Co-clustering or two-mode-clustering), clusters are modeled with both cluster members and relevant attributes.
• Group models: some algorithms (unfortunately) do not provide a refined model for their results and just provide the grouping information.

A clustering is essentially a set of such clusters, usually containing all objects in the data set. Additionally, it may specify the relationship of the clusters to each other, for example a hierarchy of clusters embedded in each other. Clusterings can be roughly distinguished in:

• hard clustering: each object belongs to a cluster or not
• soft clustering (also: fuzzy clustering): each object belongs to each cluster to a certain degree (e.g. a likelihood of belonging to the cluster)

There are also finer distinctions possible, for example:

• strict partitioning clustering: here each object belongs to exactly one cluster
• strict partitioning clustering with outliers: object can also belong to no cluster, and are considered outliers.
• overlapping clustering (also: alternative clustering, multi-view clustering): while usually a hard clustering, objects may belong to more than one cluster.
• hierarchical clustering: objects that belong to a child cluster also belong to the parent cluster
• subspace clustering: while an overlapping clustering, within a uniquely defined subspace, clusters are not expected to overlap.

Clustering Algorithms

Clustering algorithms can be categorized based on their cluster model, as listed above. The following overview will only list the most prominent examples of clustering algorithms, as there are probably a few dozen (if not over 100) published clustering algorithms. Not all provide models for their clusters and can thus not easily be categorized. An overview of algorithms explained in Wikipedia can be found in the list of statistics algorithms.

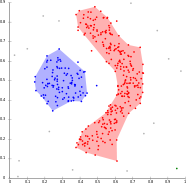
Connectivity based clustering (Hierarchical clustering)

Main article: Hierarchical clustering

Connectivity based clustering, also known as hierarchical clustering, is based on the core idea of objects being more related to nearby objects than to objects farther away. As such, these algorithms connect "objects" to form "clusters" based on their distance. A cluster can be described largely by the maximum distance needed to connect parts of the cluster. At different distances, different clusters will form, which can be represented using a dendrogram, which explains where the common name "hierarchical clustering" comes from: these algorithms do not provide a single partitioning of the data set, but instead provide an extensive hierarchy of clusters that merge with each other at certain distances. In a dendrogram, the y-axis marks the distance at which the clusters merge, while the objects are placed along the x-axis such that the clusters don't mix.

Connectivity based clustering is a whole family of methods that differ by the way distances are computed. Apart from the usual choice of distance functions, the user also needs to decide on the linkage criterion (since a cluster consists of multiple object, there are multiple candidates to compute the distance to) to use. Popular choices are known as single-linkage clustering (the minimum of object distances), complete linkage clustering (the maximum of object distances) or UPGMA ("Unweighted Pair Group Method with Arithmetic Mean", also known as average linkage clustering). Furthermore, hierarchical clustering can be computed agglomerative (starting with single elements and aggregating them into clusters) or divisive (starting with the complete data set and dividing it into partitions).

While these methods are fairly easy to understand, the results are not always easy to use, as they will not produce a unique partitioning of the data set, but a hierarchy the user still needs to choose appropriate clusters from. The methods are not very robust towards outliers, which will either show up as additional clusters or even cause other clusters to merge (known as "chaining phenomenon", in particular with single-linkage clustering). In the general case, the complexity is $\mathcal{O}(n^3)$, which makes them too slow for large data sets. For some special cases, optimal efficient methods (of complexity $\mathcal{O}(n^2)$) are known: SLINK^[1] for single-linkage and CLINK^[2] for complete-linkage clustering. In the data mining community these methods are recognized as a theoretical foundation of cluster analysis, but often considered obsolete. They did however provide inspiration for many later methods such as density based clustering.

• Linkage clustering examples
• 

  Single-linkage on Gaussian data. At 35 clusters, the biggest cluster starts fragmenting into smaller parts, while before it was still connected to the second largest due to the single-link effect.

• 

  Single-linkage on density-based clusters. 20 clusters extracted, most of which contain single elements, since linkage clustering does not have a notion of "noise".

Centroid-based clustering

Main article: k-means clustering

In centroid-based clustering, clusters are represented by a central vector, which must not necessarily be a member of the data set. When the number of clusters is fixed to k, k-means clustering gives a formal definition as an optimization problem: find the k cluster centers and assign the objects to the nearest cluster center, such that the squared distances from the cluster are minimized.

The optimization problem itself is known to be NP-hard, and thus the common approach is to search only for approximate solutions. A particularly well known approximative method is Lloyd's algorithm,^[3] often actually referred to as "k-means algoritm". It does however only find a local optimum, and is commonly run multiple times with different random initializations. Variations of k-means often include such optimizations as choosing the best of multiple runs, but also restricting the centroids to members of the data set (k-medoids), choosing medians (k-medians clustering), choosing the initial centers less randomly (K-means++) or allowing a fuzzy cluster assignment (Fuzzy c-means).

Most k-means-type algorithms require the number of clusters - k - to be specified in advance, which is considered to be one of the biggest drawbacks of these algorithms. Furthermore, the algorithms prefer clusters of approximately similar size, as they will always assign an object to the nearest centroid. This often leads to incorrectly cut borders in between of clusters (which is not surprising, as the algorithm optimized cluster centers, not cluster borders).

K-means has a number of interesting theoretical properties. On one hand, it partitions the data space into a structure known as Voronoi diagram. On the other hand, it is conceptually close to nearest neighbor classification and as such popular in machine learning. Third, it can be seen as a variation of model based classification, and Lloyd's algorithm as a variation of the Expectation-maximization algorithm for this model discussed below.

• k-Means clustering examples
• 

  K-means separates data into Voronoi-cells, which assumes equal-sized clusters (not adequate here)

• 

  K-means cannot represent density-based clusters

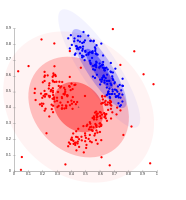
Distribution-based clustering

The clustering model most closely related to statistics is based on distribution models. Clusters can then easily be defined as objects belonging most likely to the same distribution. A nice property of this approach is that this closely resembles the way artificial data sets are generated: by sampling random objects from a distribution.

While the theoretical foundation of these methods is excellent, they suffer from one key problem known as overfitting, unless constraints are put on the model complexity. A more complex model will usually always be able to explain the data better, which makes choosing the appropriate model complexity inherently difficult.

The most prominent method is known as expectation-maximization algorithm (or short: EM-clustering). Here, the data set is usually modeled with a fixed (to avoid overfitting) number of Gaussian distributions that are initialized randomly and whose parameters are iteratively optimized to fit better to the data set. This will converge to a local optimum, so multiple runs may produce different results. In order to obtain a hard clustering, objects are often then assigned to the Gaussian distribution they most likely belong to, for soft clusterings this is not necessary.

Distribution-based clustering is a semantically strong method, as it not only provides you with clusters, but also produces complex models for the clusters that can also capture correlation and dependence of attributes. However, using these algorithms puts an extra burden on the user: to choose appropriate data models to optimize, and for many real data sets, there may be no mathematical model available the algorithm is able to optimize (e.g. assuming Gaussian distributions is a rather strong assumption on the data).

• EM clustering examples
• 

  On Gaussian-distributed data, EM works well, since it uses Gaussians for modelling clusters

• 

  Density-based clusters cannot be modeled using Gaussian distributions

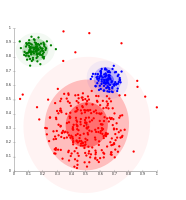
Density-based clustering

In density-based clustering^[4], clusters are defined as areas of higher density than the remainder of the data set. Objects in these sparse areas - that are required to separate clusters - are usually considered to be noise and border points.

The most popular^[5] density based clustering method is DBSCAN.^[6] In contrast to many newer methods, it features a well-defined cluster model called "density-reachability". Similar to linkage based clustering, it is based on connecting points within certain distance thresholds. However, it only connects points that satisfy a density criterion, in the original variant defined as a minimum number of other objects within this radius. A cluster consists of all density-connected objects (which can form a cluster of an arbitrary shape, in contrast to many other methods) plus all objects that are within these objects range. Another interesting property of DBSCAN is that its complexity is fairly low - it requires a linear number of range queries on the database - and that it will discover essentially the same results (it is deterministic for core and noise points, but not for border points) in each run, therefore there is no need to run it multiple times. OPTICS^[7] is a generalization of DBSCAN that removes the need to choose an appropriate value for the range parameter ε, and produces a hierarchical result related to that of linkage clustering. DeLi-Clu,^[8] Density-Link-Clustering combines ideas from single-linkage clustering and OPTICS, eliminating the ε parameter entirely and offering performance improvements over OPTICS by using an R-tree index.

The key drawback of DBSCAN and OPTICS is that they expect some kind of density drop to detect cluster borders. On data sets with e.g. overlapping Gaussian distributions - a common use case in artificial data - the cluster borders produced by these algorithms will often look arbitrary, because the cluster density decreases continuously. On a mixtures of Gaussians data set, they will almost every time be outperformed by methods such as EM clustering, that are able to precisely model this kind of data.

• density-based clustering examples
• 

  Density-based clustering with DBSCAN.

• 

  DBSCAN assumes clusters of similar density, and may have Problems separating nearby clusters

• 

  OPTICS is a DBSCAN variant that handles different densities much better

Newer Developments

In recent years considerable effort has been put into improving algorithm performance of the existing algorithms.^[9] Among the most popular^{[citation needed]} are CLARANS (Ng and Han, 1994),^[10] and BIRCH (Zhang et al., 1996).^[11] With the recent need to process larger and larger data sets (also known as big data), the willingness to treat semantic meaning of the generated clusters for performance has been increasing. This led to the development of pre-clustering methods such as canopy clustering, which can process huge data sets efficiently, but the resulting "clusters" are merely a rough pre-partitioning of the data set to then analyze the partitions with existing slower methods such as k-means clustering.

For high-dimensional data, many of the existing methods fail due to the curse of dimensionality, which renders in particular distance functions problematic in high-dimensional spaces. This led to new clustering algorithms for high-dimensional data that focus on subspace clustering (where only some attributes are used, and cluster models include the relevant attributes for the cluster) and correlation clustering that also looks for arbitrary rotated ("correlated") subspace clusters that can be modeled by giving a correlation of their attributes. Examples for such clustering algorithms are CLIQUE^[12] and SUBCLU.^[13]

Ideas from density-based clustering methods (in particular the DBSCAN/OPTICS family of algorithms) have been adopted to subspace clustering (HiSC,^[14] hierarchical subspace clustering and DiSH^[15]) and correlation clustering (HiCO,^[16] hierarchical corelation clustering, 4C^[17] using "correlation connectivity" and ERiC^[18] exploring hierarchical density-based correlation clusters).

Several different clustering systems based on mutual information have been proposed. One is Marina Meilă's variation of information metric;^[19] another provides hierarchical clustering.^[20] Using genetic algorithms, a wide range of different fit-functions can be optimized, including mutual information.^[21]

Evaluation of Clustering Results

Evaluation of clustering results sometimes is referred to as cluster validation.

There have been several suggestions for a measure of similarity between two clusterings. Such a measure can be used to compare how well different data clustering algorithms perform on a set of data. These measures are usually tied to the type of criterion being considered in assessing the quality of a clustering method.

Internal evaluation

When a clustering result is evaluated based on the data that was clustered itself, this is called internal evaluation. These methods usually assign the best score to the algorithm that produces clusters with high similarity within a cluster and low similarity between clusters. One drawback of using internal criteria in cluster evaluation is that high scores on an internal measure do not necessarily result in effective information retrieval applications.^[22] Additionally, this evaluation is biased towards algorithms that use the same cluster model. For example k-Means clustering naturally optimizes object distances, and a distance-based interal criterion will likely overrate the resulting clustering.

The following methods can be used to assess the quality clustering algorithms based on internal criterion:

• Davies–Bouldin index

The Davies–Bouldin index can be calculated by the following formula:

$DB = \frac {1} {n} \sum_{i=1}^{n} \max_{i\neq j}\left(\frac{\sigma_i + \sigma_j} {d(c_i,c_j)}\right)$

where n is the number of clusters, c_x is the centroid of cluster x, σ_x is the average distance of all elements in cluster x to centroid c_x, and d(c_i,c_j) is the distance between centroids c_i and c_j. Since algorithms that produce clusters with low intra-cluster distances (high intra-cluster similarity) and high inter-cluster distances (low inter-cluster similarity) will have a low Davies–Bouldin index, the clustering algorithm that produces a collection of clusters with the smallest Davies–Bouldin index is considered the best algorithm based on this criterion.

• Dunn index (J. C. Dunn 1974)

The Dunn index aims to identify dense and well-separated clusters. It is defined as the ratio between the minimal inter-cluster distance to maximal intra-cluster distance. For each cluster partition, the Dunn index can be calculated by the following formula ^[23]:

$D = \min_{1\leq i \leq n}\left\{\min_{1\leq j \leq n,i\neq j}\left\{\frac {d(i,j)}{\max_{1\leq k \leq n}{d^{'}(k)}}\right\}\right\}$

where d(i,j) represents the distance between clusters i and j, and d^'(k) measures the intra-cluster distance of cluster k. The inter-cluster distance d(i,j) between two clusters may be any number of distance measures, such as the distance between the centroids of the clusters. Similarly, the intra-cluster distance d^'(k) may be measured in a variety ways, such as the maximal distance between any pair of elements in cluster k. Since internal criterion seek clusters with high intra-cluster similarity and low inter-cluster similarity, algorithms that produce clusters with high Dunn index are more desirable.

External evaluation

In external evaluation, clustering results are evaluated based on data that was not used for clustering, such as known class labels and external benchmarks. Such benchmarks consist of a set of pre-classified items, and these sets are often created by human (experts). Thus, the benchmark sets can be thought of as a gold standard for evaluation. These types of evaluation methods measure how close the clustering is to the predetermined benchmark classes. However, it has recently been discussed whether this is adequate for real data, or only on synthetic data sets with a factual ground truth, since classes can contain internal structure, the attributes present may not allow separation of clusters or the classes may contain anomalies.^[24] Additionally, from a knowledge discovery point of view, the reproduction of known knowledge may not necessarily be the intended result.

Some of the measures of quality of a cluster algorithm using external criterion include:

• Rand measure (William M. Rand 1971)^[25]

The Rand index computes how similar the clusters (returned by the clustering algorithm) are to the benchmark classifications. One can also view the Rand index as a measure of the percentage of correct decisions made by the algorithm. It can be computed using the following formula:

$RI = \frac {TP + TN} {TP + FP + FN + TN}$

where TP is the number of true positives, TN is the number of true negatives, FP is the number of false positives, and FN is the number of false negatives. One issue with the Rand index is that false positives and false negatives are equally weighted. This may be an undesirable characteristic for some clustering applications. The F-measure addresses this concern.

• F-measure

The F-measure can be used to balance the contribution of false negatives by weighting recall through a parameter $\beta \geq 0$. Let precision and recall be defined as follows:

$P = \frac {TP } {TP + FP }$

$R = \frac {TP } {TP + FN}$

where P is the precision rate and R is the recall rate. We can calculate the F-measure by using the following formula ^[22]:

$F_{\beta} = \frac {(\beta^2 + 1)\cdot P \cdot R } {\beta^2 \cdot P + R}$

Notice that when β = 0, F₀ = P. In other words, recall has no impact on the F-measure when β = 0, and increasing β allocates an increasing amount of weight to recall in the final F-measure.

• Pair-counting F-Measure is the F-Measure applied to the set of object pairs, where objects are paired with each other when they are part of the same cluster. This measure is able to compare clusterings with different numbers of clusters.
• Jaccard index

The Jaccard index is used to quantify the similarity between two datasets. The Jaccard index takes on a value between 0 and 1. An index of 1 means that the two dataset are identical, and an index of 0 indicates that the datasets have no common elements. The Jaccard index is defined by the following formula:

$J(A,B) = \frac {|A \cap B| } {|A \cup B|}$

This is simply the number of unique elements common to both sets divided by the total number of unique elements in both sets.

• Fowlkes–Mallows index (E. B. Fowlkes & C. L. Mallows 1983)^[26]
• Confusion matrix

A confusion matrix can be used to quickly visualize the results of a classification (or clustering) algorithm. It shows how different a cluster is different from the gold standard cluster.

• The Mutual Information is an information theoretic measure of how much information is shared between a clustering and a ground-truth classification that can detect a non-linear similarity between two clusterings. Adjusted mutual information is the corrected-for-chance variant of this that has a reduced bias for varying cluster numbers.

Applications

Biology, computational biology and bioinformatics

Plant and animal ecology

cluster anaysis is used to describe and to make spatial and temporal comparisons of communities (assemblages) of organisms in heterogeneous environments; it is also used in plant systematics to generate artificial phylogenies or clusters of organisms (individuals) at the species, genus or higher level that share a number of attributes

Transcriptomics

clustering is used to build groups of genes with related expression patterns (also known as coexpressed genes). Often such groups contain functionally related proteins, such as enzymes for a specific pathway, or genes that are co-regulated. High throughput experiments using expressed sequence tags (ESTs) or DNA microarrays can be a powerful tool for genome annotation, a general aspect of genomics.

Sequence analysis

clustering is used to group homologous sequences into gene families. This is a very important concept in bioinformatics, and evolutionary biology in general. See evolution by gene duplication.

High-throughput genotyping platforms

clustering algorithms are used to automatically assign genotypes.

Human genetic clustering

The similarity of genetic data is used in clustering to infer population structures.

Medicine

Medical imaging

On PET scans, cluster analysis can be used to differentiate between different types of tissue and blood in a three dimensional image. In this application, actual position does not matter, but the voxel intensity is considered as a vector, with a dimension for each image that was taken over time. This technique allows, for example, accurate measurement of the rate a radioactive tracer is delivered to the area of interest, without a separate sampling of arterial blood, an intrusive technique that is most common today.

IMRT segmentation

Clustering can be used to divide a fluence map into distinct regions for conversion into deliverable fields in MLC-based Radiation Therapy.

Business and marketing

Market research

Cluster analysis is widely used in market research when working with multivariate data from surveys and test panels. Market researchers use cluster analysis to partition the general population of consumers into market segments and to better understand the relationships between different groups of consumers/potential customers, and for use in market segmentation, Product positioning, New product development and Selecting test markets.

Grouping of Shopping Items

Clustering can be used to group all the shopping items available on the web into a set of unique products. For example, all the items on eBay can be grouped into unique products. (eBay doesn't have the concept of a SKU)

World wide web

Social network analysis

In the study of social networks, clustering may be used to recognize communities within large groups of people.

Search result grouping

In the process of intelligent grouping of the files and websites, clustering may be used to create a more relevant set of search results compared to normal search engines like Google. There are currently a number of web based clustering tools such as Clusty.

Slippy map optimization

Flickr's map of photos and other map sites use clustering to reduce the number of markers on a map. This makes it both faster and reduces the amount of visual clutter.

Computer science

Software evolution

Clustering is useful in software evolution as it helps to reduce legacy properties in code by reforming functionality that has become dispersed. It is a form of restructuring and hence is a way of directly preventative maintenance.

Image segmentation

Clustering can be used to divide a digital image into distinct regions for border detection or object recognition.

Evolutionary algorithms

Clustering may be used to identify different niches within the population of an evolutionary algorithm so that reproductive opportunity can be distributed more evenly amongst the evolving species or subspecies.

Recommender systems

Recommender systems are designed to recommend new items based on a user's tastes. They sometimes use clustering algorithms to predict a user's preferences based on the preferences of other users in the user's cluster.

Social science

Crime Analysis

Cluster analysis can be used to identify areas where there are greater incidences of particular types of crime. By identifying these distinct areas or "hot spots" where a similar crime has happened over a period of time, it is possible to manage law enforcement resources more effectively.

Educational data mining

Cluster analysis is for example used to identify groups of schools or students with similar properties.

Others

Mathematical chemistry

To find structural similarity, etc., for example, 3000 chemical compounds were clustered in the space of 90 topological indices.^[27]

Climatology

To find weather regimes or preferred sea level pressure atmospheric patterns.^[28]

Petroleum Geology

Cluster Analysis is used to reconstruct missing bottom hole core data or missing log curves in order to evaluate reservoir properties.

Physical Geography

The clustering of chemical properties in different sample locations.

See also

Related topics

Main article: Data mining

Clustering high-dimensional data Curse of dimensionality

Data stream clustering Dimension reduction

Silhouette Parallel coordinates

Related methods

See also Category: Data clustering algorithms.

Artificial neural network (ANN) Cluster-weighted modeling Consensus clustering Constrained clustering

Latent Class Analysis Multidimensional scaling Nearest neighbor search

Neighbourhood components analysis Paired difference test Principal Component Analysis Structured data analysis (statistics)

References

1. ^ R. Sibson (1973). "SLINK: an optimally efficient algorithm for the single-link cluster method". The Computer Journal (British Computer Society) 16 (1): 30–34. http://www.cs.gsu.edu/~wkim/index_files/papers/sibson.pdf. 
2. ^ D. Defays (1977). "An efficient algorithm for a complete link method". The Computer Journal (British Computer Society) 20 (4): 364–366. 
3. ^ Lloyd, S. (1982). "Least squares quantization in PCM". IEEE Transactions on Information Theory 28 (2): 129–137. doi:10.1109/TIT.1982.1056489.  edit
4. ^ Hans-Peter Kriegel, Peer Kröger, Jörg Sander, Arthur Zimek (2011). "Density-based Clustering". WIREs Data Mining and Knowledge Discovery 1 (3): 231-240. doi:10.1002/widm.30. http://wires.wiley.com/WileyCDA/WiresArticle/wisId-WIDM30.html. 
5. ^ Microsoft academic search: most cited data mining articles: DBSCAN is on rank 24, when accessed on: 4/18/2010
6. ^ Martin Ester, Hans-Peter Kriegel, Jörg Sander, Xiaowei Xu (1996). "A density-based algorithm for discovering clusters in large spatial databases with noise". In Evangelos Simoudis, Jiawei Han, Usama M. Fayyad. Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96). AAAI Press. pp. 226–231. ISBN 1-57735-004-9. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.71.1980. 
7. ^ Mihael Ankerst, Markus M. Breunig, Hans-Peter Kriegel, Jörg Sander (1999). "OPTICS: Ordering Points To Identify the Clustering Structure". ACM SIGMOD international conference on Management of data. ACM Press. pp. 49–60. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.129.6542. 
8. ^ Achtert, E.; Böhm, C.; Kröger, P. (2006). "DeLi-Clu: Boosting Robustness, Completeness, Usability, and Efficiency of Hierarchical Clustering by a Closest Pair Ranking". LNCS: Advances in Knowledge Discovery and Data Mining 3918: 119–128. doi:10.1007/11731139_16.  edit
9. ^ Z. Huang. "Extensions to the k-means algorithm for clustering large data sets with categorical values". Data Mining and Knowledge Discovery, 2:283–304, 1998.
10. ^ R. Ng and J. Han. "Efficient and effective clustering method for spatial data mining". In: Proceedings of the 20th VLDB Conference, pages 144-155, Santiago, Chile, 1994.
11. ^ Tian Zhang, Raghu Ramakrishnan, Miron Livny. "An Efficient Data Clustering Method for Very Large Databases." In: Proc. Int'l Conf. on Management of Data, ACM SIGMOD, pp. 103–114.
12. ^ Agrawal, R.; Gehrke, J.; Gunopulos, D.; Raghavan, P. (2005). "Automatic Subspace Clustering of High Dimensional Data". Data Mining and Knowledge Discovery 11: 5. doi:10.1007/s10618-005-1396-1.  edit
13. ^ Karin Kailing, Hans-Peter Kriegel and Peer Kröger. Density-Connected Subspace Clustering for High-Dimensional Data. In: Proc. SIAM Int. Conf. on Data Mining (SDM'04), pp. 246-257, 2004.
14. ^ Achtert, E.; Böhm, C.; Kriegel, H. P.; Kröger, P.; Müller-Gorman, I.; Zimek, A. (2006). "Finding Hierarchies of Subspace Clusters". LNCS: Knowledge Discovery in Databases: PKDD 2006 4213: 446–453. doi:10.1007/11871637_42.  edit
15. ^ Achtert, E.; Böhm, C.; Kriegel, H. P.; Kröger, P.; Müller-Gorman, I.; Zimek, A. (2007). "Detection and Visualization of Subspace Cluster Hierarchies". LNCS: Advances in Databases: Concepts, Systems and Applications 4443: 152–163. doi:10.1007/978-3-540-71703-4_15.  edit
16. ^ Achtert, E.; Böhm, C.; Kröger, P.; Zimek, A. (2006). "Mining Hierarchies of Correlation Clusters". Proc. 18th International Conference on Scientific and Statistical Database Management (SSDBM): 119–128. doi:10.1109/SSDBM.2006.35.  edit
17. ^ Böhm, C.; Kailing, K.; Kröger, P.; Zimek, A. (2004). "Computing Clusters of Correlation Connected objects". Proceedings of the 2004 ACM SIGMOD international conference on Management of data - SIGMOD '04. pp. 455. doi:10.1145/1007568.1007620. ISBN 1581138598.  edit
18. ^ Achtert, E.; Bohm, C.; Kriegel, H. P.; Kroger, P.; Zimek, A. (2007). "On Exploring Complex Relationships of Correlation Clusters". 19th International Conference on Scientific and Statistical Database Management (SSDBM 2007). pp. 7. doi:10.1109/SSDBM.2007.21. ISBN 0-7695-2868-6.  edit
19. ^ Meilă, Marina (2003). "Comparing Clusterings by the Variation of Information". Learning Theory and Kernel Machines: 173–187. 
20. ^ Alexander Kraskov, Harald Stögbauer, Ralph G. Andrzejak, and Peter Grassberger, "Hierarchical Clustering Based on Mutual Information", (2003) ArXiv q-bio/0311039
21. ^ Auffarth, B. (2010). Clustering by a Genetic Algorithm with Biased Mutation Operator. WCCI CEC. IEEE, July 18–23, 2010. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.170.869
22. ^ ^{a b} Christopher D. Manning, Prabhakar Raghavan & Hinrich Schutze. Introduction to Information Retrieval. Cambridge University Press. ISBN 978-0-521-86571-5. 
23. ^ Dunn, J. (1974). "Well separated clusters and optimal fuzzy partitions". Journal of Cybernetics 4: 95–104. doi:10.1080/01969727408546059. 
24. ^ Ines Färber, Stephan Günnemann, Hans-Peter Kriegel, Peer Kröger, Emmanuel Müller, Erich Schubert, Thomas Seidl, Arthur Zimek (2010). "On Using Class-Labels in Evaluation of Clusterings". In Xiaoli Z. Fern, Ian Davidson, Jennifer Dy. MultiClust: Discovering, Summarizing, and Using Multiple Clusterings. ACM SIGKDD. http://eecs.oregonstate.edu/research/multiclust/Evaluation-4.pdf. 
25. ^ W. M. Rand (1971). "Objective criteria for the evaluation of clustering methods". Journal of the American Statistical Association (American Statistical Association) 66 (336): 846–850. doi:10.2307/2284239. JSTOR 2284239. 
26. ^ E. B. Fowlkes & C. L. Mallows (1983), "A Method for Comparing Two Hierarchical Clusterings", Journal of the American Statistical Association 78, 553–569.
27. ^ Basak S.C., Magnuson V.R., Niemi C.J., Regal R.R. "Determing Structural Similarity of Chemicals Using Graph Theoretic Indices". Discr. Appl. Math., 19, 1988: 17-44.
28. ^ Huth R. et al. "Classifications of Atmospheric Circulation Patterns: Recent Advances and Applications". Ann. N.Y. Acad. Sci., 1146, 2008: 105-152