- DBSCAN
-
DBSCAN (for density-based spatial clustering of applications with noise) is a data clustering algorithm proposed by Martin Ester, Hans-Peter Kriegel, Jörg Sander and Xiaowei Xu in 1996.[1] It is a density-based clustering algorithm because it finds a number of clusters starting from the estimated density distribution of corresponding nodes. DBSCAN is one of the most common clustering algorithms and also most cited in scientific literature.[2] OPTICS can be seen as a generalization of DBSCAN to multiple ranges, effectively replacing the ε parameter with a maximum search radius.
Contents
Basic idea
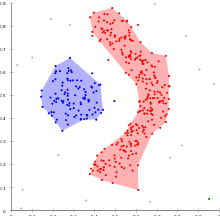
DBSCAN's definition of a cluster is based on the notion of density reachability. Basically, a point q is directly density-reachable from a point p if it is not farther away than a given distance ε (i.e., is part of its ε-neighborhood), and if p is surrounded by sufficiently many points such that one may consider p and q be part of a cluster. q is called density-reachable (note: this is different from "directly density-reachable") from p if there is a sequence
 of points with p1 = p and pn = q where each pi + 1 is directly density-reachable from pi. Note that the relation of density-reachable is not symmetric (since q might lie on the edge of a cluster, having insufficiently many neighbors to count as a genuine cluster element), so the notion of density-connected is introduced: two points p and q are density-connected if there is a point o such that both p and q are density reachable from o.
of points with p1 = p and pn = q where each pi + 1 is directly density-reachable from pi. Note that the relation of density-reachable is not symmetric (since q might lie on the edge of a cluster, having insufficiently many neighbors to count as a genuine cluster element), so the notion of density-connected is introduced: two points p and q are density-connected if there is a point o such that both p and q are density reachable from o.A cluster, which is a subset of the points of the database, satisfies two properties:
- All points within the cluster are mutually density-connected.
- If a point is density-connected to any point of the cluster, it is part of the cluster as well.
Algorithm
DBSCAN requires two parameters: ε (eps) and the minimum number of points required to form a cluster (minPts). It starts with an arbitrary starting point that has not been visited. This point's ε-neighborhood is retrieved, and if it contains sufficiently many points, a cluster is started. Otherwise, the point is labeled as noise. Note that this point might later be found in a sufficiently sized ε-environment of a different point and hence be made part of a cluster.
If a point is found to be part of a cluster, its ε-neighborhood is also part of that cluster. Hence, all points that are found within the ε-neighborhood are added, as is their own ε-neighborhood. This process continues until the cluster is completely found. Then, a new unvisited point is retrieved and processed, leading to the discovery of a further cluster or noise.
Pseudocode
DBSCAN(D, eps, MinPts) C = 0 for each unvisited point P in dataset D mark P as visited N = regionQuery(P, eps) if sizeof(N) < MinPts mark P as NOISE else C = next cluster expandCluster(P, N, C, eps, MinPts) expandCluster(P, N, C, eps, MinPts) add P to cluster C for each point P' in N if P' is not visited mark P' as visited N' = regionQuery(P', eps) if sizeof(N') >= MinPts N = N joined with N' if P' is not yet member of any cluster add P' to cluster CComplexity
DBSCAN visits each point of the database, possibly multiple times (e.g., as candidates to different clusters). For practical considerations, however, the time complexity is mostly governed by the number of regionQuery invocations. DBSCAN executes exactly one such query for each point, and if an indexing structure is used that executes such a neighborhood query in O(log n), an overall runtime complexity of
 is obtained. Without the use of an accelerating index structure, the run time complexity is O(n2). Often the distance matrix of size (n2 − n) / 2 is materialized to avoid distance recomputations. This however also needs O(n2) memory.
is obtained. Without the use of an accelerating index structure, the run time complexity is O(n2). Often the distance matrix of size (n2 − n) / 2 is materialized to avoid distance recomputations. This however also needs O(n2) memory.Advantages
- DBSCAN does not require you to know the number of clusters in the data a priori, as opposed to k-means.
- DBSCAN can find arbitrarily shaped clusters. It can even find clusters completely surrounded by (but not connected to) a different cluster. Due to the MinPts parameter, the so-called single-link effect (different clusters being connected by a thin line of points) is reduced.
- DBSCAN has a notion of noise.
- DBSCAN requires just two parameters and is mostly insensitive to the ordering of the points in the database. (Only points sitting on the edge of two different clusters might swap cluster membership if the ordering of the points is changed, and the cluster assignment is unique only up to isomorphism.)
Disadvantages
- DBSCAN can only result in a good clustering as good as its distance measure is in the function regionQuery(P,ε). The most common distance metric used is the euclidean distance measure. Especially for high-dimensional data, this distance metric can be rendered almost useless due to the so called "Curse of dimensionality", rendering it hard to find an appropriate value for ε. This effect however is present also in any other algorithm based on the euclidean distance.
- DBSCAN cannot cluster data sets well with large differences in densities, since the minPts-ε combination cannot be chosen appropriately for all clusters then.
See the section on extensions below for algorithmic modifications to handle these issues.
Parameter estimation
Every data mining task has the problem of parameters. Every parameter influences the algorithm in specific ways. For DBSCAN the parameters ε and MinPts are needed. The parameters must be specified by the user of the algorithms since other data sets and other questions require different parameters. An initial value for ε can be determined by a k-distance graph. As a rule of thumb, k can be derived from the number of dimensions in the data set D as
 . However, larger values are usually better for data sets with noise.
. However, larger values are usually better for data sets with noise.Although this parameter estimation gives a sufficient initial parameter set the resulting clustering can turn out to be not the expected partitioning. Therefore research has been performed on incrementally optimizing the parameters against a specific target value.
OPTICS can be seen as a generalization of DBSCAN that replaces the ε parameter with a maximum value that mostly effects performance. MinPts then essentially becomes the minimum cluster size to find. While the algorithm is a lot easier to parameterize then DBSCAN, the results are a bit more difficult to use, as it will usually produce a hierarchical clustering instead of the simple data partitioning that DBSCAN produces.
Generalization
Generalized DBSCAN or GDBSCAN [3][4] is a generalization by the same authors to arbitrary "neighborhood" and "dense" predicates. The ε and minpts parameters are removed from the original algorithm and moved to the predicates. For example on polygon data, the "neighborhood" could be any intersecting polygon, whereas the density predicate uses the polygon areas instead of just the object count.
Extensions
The basic DBSCAN algorithm has been used as a base for many other developments, such as parallelisation by Domenica Arlia and Massimo Coppola or an enhancement of the data set background to support uncertain data presented by Dirk Habich and Peter Benjamin Volk. The basic idea has been extended to hierarchical clustering by the OPTICS algorithm. DBSCAN is also used as part of subspace clustering algorithms like PreDeCon and SUBCLU.
Availability
An example implementation of DBSCAN is available in the ELKI framework. Notice that this implementation is not optimized for speed but for extensibility. Thus, this implementation can use various index structures for sub-quadratic performance and supports various distance functions and arbitrary data types, but it may be outperformed by low-level optimized implementations on small data sets.
External links
- DBSCAN clustering using C++ by Antonio Gulli (No index support, quadratic time and memory complexity, vector data only, some distance functions)
- R package fpc includes DBSCAN (No index support, quadratic complexity, accepts distance matrices)
References
- ^ Martin Ester, Hans-Peter Kriegel, Jörg Sander, Xiaowei Xu (1996-). "A density-based algorithm for discovering clusters in large spatial databases with noise". In Evangelos Simoudis, Jiawei Han, Usama M. Fayyad. Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96). AAAI Press. pp. 226–231. ISBN 1-57735-004-9. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.71.1980.
- ^ [1] Most cited data mining articles according to Microsoft academic search; DBSCAN is on rank 24, when accessed on: 4/18/2010
- ^ Sander, Jörg; Ester, Martin; Kriegel, Hans-Peter; Xu, Xiaowei (1998). "Density-Based Clustering in Spatial Databases: The Algorithm GDBSCAN and Its Applications". Data Mining and Knowledge Discovery (Berlin: Springer-Verlag) 2 (2): 169–194. doi:10.1023/A:1009745219419. http://www.springerlink.com/content/n22065n21n1574k6.
- ^ Sander, Jörg (1998). Generalized Density-Based Clustering for Spatial Data Mining. München: Herbert Utz Verlag. ISBN 3896754696.
Further reading
- Domenica Arlia, Massimo Coppola. "Experiments in Parallel Clustering with DBSCAN". Euro-Par 2001: Parallel Processing: 7th International Euro-Par Conference Manchester, UK August 28–31, 2001, Proceedings. Springer Berlin.
Categories:- Data clustering algorithms
Wikimedia Foundation. 2010.