NP-hard

For a gentler introduction, see P versus NP problem.

Euler diagram for P, NP, NP-complete, and NP-hard set of problems

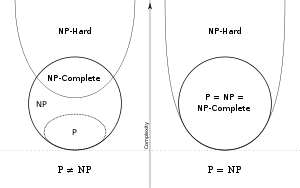
NP-hard (non-deterministic polynomial-time hard), in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H (i.e., L ≤ _TH). In other words, L can be solved in polynomial time by an oracle machine with an oracle for H. Informally, we can think of an algorithm that can call such an oracle machine as a subroutine for solving H, and solves L in polynomial time, if the subroutine call takes only one step to compute. NP-hard problems may be of any type: decision problems, search problems, or optimization problems.

As consequences of definition, we have (note that these are claims, not definitions):

• Problem H is at least as hard as L, because H can be used to solve L;

• Since L is NP-complete, and hence the hardest in class NP, also problem H is at least as hard as NP, but H does not have to be in NP and hence does not have to be a decision problem (even if it is a decision problem, it need not be in NP);

• Since NP-complete problems transform to each other by polynomial-time many-one reduction (also called polynomial transformation), all NP-complete problems can be solved in polynomial time by a reduction to H, thus all problems in NP reduce to H; note, however, that this involves combining two different transformations: from NP-complete decision problems to NP-complete problem L by polynomial transformation, and from L to H by polynomial Turing reduction;

• If there is a polynomial algorithm for any NP-hard problem, then there are polynomial algorithms for all problems in NP, and hence P = NP;

• If P ≠ NP, then NP-hard problems have no solutions in polynomial time, while P = NP does not resolve whether the NP-hard problems can be solved in polynomial time;

• If an optimization problem H has an NP-complete decision version L, then H is NP-hard.

A common mistake is to think that the NP in NP-hard stands for non-polynomial. Although it is widely suspected that there are no polynomial-time algorithms for NP-hard problems, this has never been proven. Moreover, the class NP also contains all problems which can be solved in polynomial time.

Examples

An example of an NP-hard problem is the decision subset sum problem, which is this: given a set of integers, does any non-empty subset of them add up to zero? That is a decision problem, and happens to be NP-complete. Another example of an NP-hard problem is the optimization problem of finding the least-cost cyclic route through all nodes of a weighted graph. This is commonly known as the traveling salesman problem.

There are decision problems that are NP-hard but not NP-complete, for example the halting problem. This is the problem which asks "given a program and its input, will it run forever?" That's a yes/no question, so this is a decision problem. It is easy to prove that the halting problem is NP-hard but not NP-complete. For example, the Boolean satisfiability problem can be reduced to the halting problem by transforming it to the description of a Turing machine that tries all truth value assignments and when it finds one that satisfies the formula it halts and otherwise it goes into an infinite loop. It is also easy to see that the halting problem is not in NP since all problems in NP are decidable in a finite number of operations, while the halting problem, in general, is not. There are also NP-hard problems that are neither NP-complete nor undecidable. For instance, the language of True quantified Boolean formulas is decidable in polynomial space, but not non-deterministic polynomial time (unless NP = PSPACE).

Alternative definitions

An alternative definition of NP-hard that is often used restricts NP-hard to decision problems and then uses polynomial-time many-one reduction instead of Turing reduction. So, formally, a language L is NP-hard if ∀L^' ∈ NP, L^' ≤ L. If it is also the case that L is in NP, then L is called NP-complete.

NP-naming convention

The NP-family naming system is confusing: NP-hard problems are not all NP, despite having NP as the prefix of their class name. However, the names are now entrenched and unlikely to change. On the other hand, the NP-naming system has some deeper sense, because the NP family is defined in relation to the class NP:

NP-hard

At least as hard as the hardest problems in NP. Such problems need not be in NP; indeed, they may not even be decision problems.

NP-complete

These are the hardest problems in NP. Such a problem is NP-hard and in NP.

NP-easy

At most as hard as NP, but not necessarily in NP, since they may not be decision problems.

NP-equivalent

Exactly as difficult as the hardest problems in NP, but not necessarily in NP.

References

• Michael R. Garey and David S. Johnson (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman. ISBN 0-7167-1045-5. http://www.amazon.com/dp/0716710455.