PSPACE

Unsolved problems in computer science

Is P = PSPACE ?

PSPACE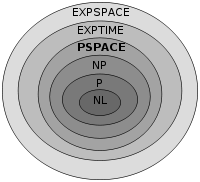
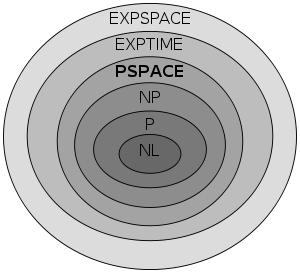
Polynomial space Defined in: External pages: Complexity Zoo Complete class: PSPACE-complete Complement class: self Equalities: AP,[1] BPPSPACE,[2] IP,[3] NPSPACE,[4] PPSPACE,[5] SAPTIME[5] DTIME: Related: PTIME Proper supersets: EXPSPACE[6] Improper supersets: AlmostPSPACE,[7] EXPTIME, RG, QPSPACE[8] Inequalities: P-close, P/log Improper subsets: CH,[9] P^PP,[10] P^#P,[10] QSZK, RG[1] Proper subsets: NL[6] Canonical problems: QSAT Properties: Syntactic Low with: self Low for: self Closed reductions: Poly-time Models of Comp: Alternating Turing machine, Turing machine

In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.

Formal definition

If we denote by SPACE(t(n)), the set of all problems that can be solved by Turing machines using at most t(n) space for some function t of the input size n, then we can define PSPACE formally as

$\mbox{PSPACE} = \bigcup_{k\in\mathbb{N}} \mbox{SPACE}(n^k)$

PSPACE is a strict superset of the set of context-sensitive languages.

It turns out that allowing the Turing machine to be nondeterministic does not add any extra power. Because of Savitch's theorem, NPSPACE is equivalent to PSPACE, essentially because a deterministic Turing machine can simulate a nondeterministic Turing machine without needing much more space (even though it may use much more time). Also, the complements of all problems in PSPACE are also in PSPACE, meaning that Co-PSPACE = PSPACE.

Relation among other classes

A representation of the relation among complexity classes

The following relations are known between PSPACE and the complexity classes NL, P, NP, PH, EXPTIME and EXPSPACE (note that $\subsetneq$ is not $\not\subseteq$):

$\mbox{NL} \subseteq \mbox{P} \subseteq \mbox{NP} \subseteq \mbox{PH} \subseteq \mbox{PSPACE}$

$\mbox{PSPACE} \subseteq \mbox{EXPTIME} \subseteq \mbox{EXPSPACE}$

$\mbox{NL} \subsetneq \mbox{PSPACE} \subsetneq \mbox{EXPSPACE}$

It is known that in the first and second line, at least one of the set containments must be strict, but it is not known which. It is widely suspected that all are strict.

The containments in the third line are both known to be strict. The first follows from direct diagonalization (the space hierarchy theorem, $\mbox{NL} \subsetneq \mbox{NPSPACE}$) and the fact that PSPACE = NPSPACE via Savitch's theorem. The second follows simply from the space hierarchy theorem.

The hardest problems in PSPACE are the PSPACE-Complete problems. See PSPACE-Complete for examples of problems that are suspected to be in PSPACE but not in NP.

Other characterizations

An alternative characterization of PSPACE is the set of problems decidable by an alternating Turing machine in polynomial time, sometimes called APTIME or just AP.

A logical characterization of PSPACE from descriptive complexity theory is that it is the set of problems expressible in second-order logic with the addition of a transitive closure operator. A full transitive closure is not needed; a commutative transitive closure and even weaker forms suffice. It is the addition of this operator that (possibly) distinguishes PSPACE from PH.

A major result of complexity theory is that PSPACE can be characterized as all the languages recognizable by a particular interactive proof system, the one defining the class IP. In this system, there is an all-powerful prover trying to convince a randomized polynomial-time verifier that a string is in the language. It should be able to convince the verifier with high probability if the string is in the language, but should not be able to convince it except with low probability if the string is not in the language.

PSPACE can be characterized as the quantum complexity class QIP.^[11]

PSPACE-completeness

Main article: PSPACE-complete

A language B is PSPACE-complete if it is in PSPACE and it is PSPACE-hard, which means for all A $\in$ PSPACE, A $\leq_p$ B, where A $\leq_p$ B means that there is a polynomial-time many-one reduction from A to B. PSPACE-complete problems are of great importance to studying PSPACE problems because they represent the most difficult problems in PSPACE. Finding a simple solution to a PSPACE-complete problem would mean we have a simple solution to all other problems in PSPACE because all PSPACE problems could be reduced to a PSPACE-complete problem. A problem can be PSPACE-hard but not PSPACE-complete because it may not be in PSPACE. For example, the halting problem is PSPACE-hard, but not PSPACE-complete.

References

1. ^ Chandra, A.K. and Kozen, D.C. and Stockmeyer, L.J., 'Alternation', Journal of the ACM, Volume 28, Issue 1, pp. 114-133, 1981.
2. ^ Complexity Zoo, [1]. Retrieved Mars 25, 2009.
3. ^ Adi Shamir. IP = PSPACE. Journal of the ACM, volume 39, issue 4, p.869–877. October 1992.
4. ^ Savitch's theorem
5. ^ ^{a b} Christos Papadimitriou (1985). "Games against Nature". "Journal of Computer and System Sciences" 31. 
6. ^ ^{a b} Space hierarchy theorem
7. ^ Definition of Almost-PSPACE. PSPACE ⊆ PSPACE^A for every A.
8. ^ Greg Kuperberg, Complexity Zoology: Active Inclusion Diagram, 2006, http://www.math.ucdavis.edu/~greg/zoology/diagram.xml
9. ^ K. W. Wagner (1986). "The complexity of combinatorial problems with succinct representation". Informatica 23: 325–356. 
10. ^ ^{a b} S. Toda (1989). "On the computational power of PP and ⊕P". FOCS 1989: 514–519. 
11. ^ QIP = PSPACE, Rahul Jain, Zhengfeng Ji, Sarvagya Upadhyay, John Watrous arXiv:0907.4737 (July 2009)

• Complexity Zoo: PSPACE
• Michael Sipser (1997). Introduction to the Theory of Computation. PWS Publishing. ISBN 0-534-94728-X.  Section 8.2–8.3 (The Class PSPACE, PSPACE-completeness), pp. 281–294.
• Christos Papadimitriou (1993). Computational Complexity (1st edition ed.). Addison Wesley. ISBN 0-201-53082-1.  Chapter 19: Polynomial space, pp. 455–490.
• Michael Sipser (2006). Introduction to the Theory of Computation (2nd edition ed.). Thomson Course Technology. ISBN 0-534-95097-3.  Chapter 8: Space Complexity

External links

• Lecture slides on space complexity From University of Toronto
• Lecture slides on space complexity From Princeton University