Nakagami distribution

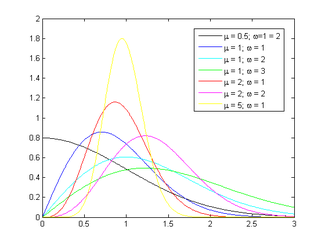
Nakagami

Probability density function
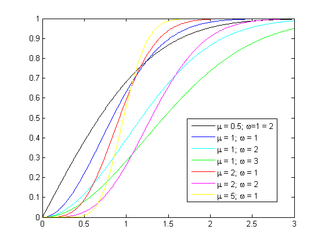
Cumulative distribution function
parameters:	μ > = 0.5 shape (real) ω > 0 spread (real)
support:	$x > 0\!$
pdf:	$\frac{2\mu^\mu}{\Gamma(\mu)\omega^\mu} x^{2\mu-1} \exp\left(-\frac{\mu}{\omega}x^2 \right)$
cdf:	$\frac{\gamma \left(\mu,\frac{\mu}{\omega} x^2\right)}{\Gamma(\mu)}$
mean:	$\frac{\Gamma(\mu+\frac{1}{2})}{\Gamma(\mu)}\left(\frac{\omega}{\mu}\right)^{1/2}$
median:	$\sqrt{\omega}\!$
mode:	$\frac{\sqrt{2}}{2} \left(\frac{(2\mu-1)\omega}{\mu}\right)^{1/2}$
variance:	$\omega\left(1-\frac{1}{\mu}\left(\frac{\Gamma(\mu+\frac{1}{2})}{\Gamma(\mu)}\right)^2\right)$

The Nakagami distribution or the Nakagami-m distribution is a probability distribution related to the gamma distribution. It has two parameters: a shape parameter μ and a second parameter controlling spread, ω.

Characterization

Its probability density function (pdf) is^[1]

$f(x;\,\mu,\omega) = \frac{2\mu^\mu}{\Gamma(\mu)\omega^\mu}x^{2\mu-1}\exp\left(-\frac{\mu}{\omega}x^2\right).$

Its cumulative distribution function is^[1]

$F(x;\,\mu,\omega) = P\left(\mu, \frac{\mu}{\omega}x^2\right)$

where P is the incomplete gamma function (regularized).

Parameter estimation

The parameters μ and ω are^[2]

$\mu = \frac{\operatorname{E}^2 \left[X^2 \right]} {\operatorname{Var} \left[X^2 \right]},$

and

$\omega = \operatorname{E} \left[X^2 \right].$

Generation

The Nakagami distribution is related to the gamma distribution. In particular, given a random variable $Y \, \sim \textrm{Gamma}(k, \theta)$, it is possible to obtain a random variable $X \, \sim \textrm{Nakagami} (\mu, \omega)$, by setting k = μ, θ = ω / μ, and taking the square root of Y:

$X = \sqrt{Y} \,$.

When 2μ is an integer, the Nakagami distribution $f(y; \,\mu,\omega)$ can be generated from the Chi distribution with parameter k set to 2μ and then following it by the scaling transformation:^{[citation needed]}

$y = \sqrt{(\omega / 2 \mu)} x.$

History and applications

The Nakagami distribution is relatively new, being first proposed in 1960.^[3] It has been used to model attenuation of wireless signals traversing multiple paths.^[4]

References

1. ^ ^{a b} Laurenson, Dave (1994). "Nakagami Distribution". Indoor Radio Channel Propagation Modelling by Ray Tracing Techniques. http://www.see.ed.ac.uk/~dil/thesis_mosaic/section2_19.html. Retrieved 2007-08-04. 
2. ^ R. Kolar, R. Jirik, J. Jan (2004) "Estimator Comparison of the Nakagami-m Parameter and Its Application in Echocardiography", Radioengineering, 13 (1), 8–12
3. ^ M. Nakagami. "The m-Distribution, a general formula of intensity of rapid fading". In William C. Hoffman, editor, Statistical Methods in Radio Wave Propagation: Proceedings of a Symposium held June 18-20, 1958, pp 3-36. Permagon Press, 1960.
4. ^ J. D. Parsons, The Mobile Radio Propagation Channel. New York: Wiley, 1992.