Chi distribution

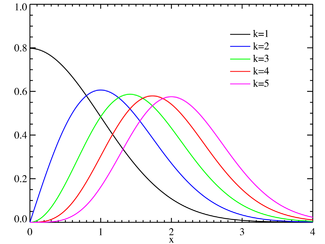
chi

Probability density function
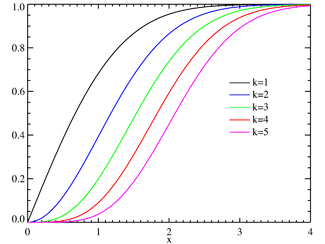
Cumulative distribution function
parameters:	$k>0\,$ (degrees of freedom)
support:	$x\in [0;\infty)$
pdf:	$\frac{2^{1-k/2}x^{k-1}e^{-x^2/2}}{\Gamma(k/2)}$
cdf:	$P(k/2,x^2/2)\,$
mean:	$\mu=\sqrt{2}\,\frac{\Gamma((k+1)/2)}{\Gamma(k/2)}$
mode:	$\sqrt{k-1}\,$ for $k\ge 1$
variance:	$\sigma^2=k-\mu^2\,$
skewness:	$\gamma_1=\frac{\mu}{\sigma^3}\,(1-2\sigma^2)$
ex.kurtosis:	$\frac{2}{\sigma^2}(1-\mu\sigma\gamma_1-\sigma^2)$
entropy:	$\ln(\Gamma(k/2))+\,$ $\frac{1}{2}(k\!-\!\ln(2)\!-\!(k\!-\!1)\psi_0(k/2))$
mgf:	Complicated (see text)
cf:	Complicated (see text)

In probability theory and statistics, the chi distribution is a continuous probability distribution. It is the distribution of the square root of the sum of squares of independent random variables having a standard normal distribution. The most familiar example is the Maxwell distribution of (normalized) molecular speeds which is a chi distribution with 3 degrees of freedom (one for each spatial coordinate). If X_i are k independent, normally distributed random variables with means μ_i and standard deviations σ_i, then the statistic

$Y = \sqrt{\sum_{i=1}^k \left(\frac{X_i-\mu_i}{\sigma_i}\right)^2}$

is distributed according to the chi distribution. The chi distribution has one parameter: k which specifies the number of degrees of freedom (i.e. the number of X_i).

Characterization

Probability density function

The probability density function is

$f(x;k) = \frac{2^{1-\frac{k}{2}}x^{k-1}e^{-\frac{x^2}{2}}}{\Gamma(\frac{k}{2})}$

where Γ(z) is the Gamma function.

Cumulative distribution function

The cumulative distribution function is given by:

$F(x;k)=P(k/2,x^2/2)\,$

where P(k,x) is the regularized Gamma function.

Generating functions

Moment generating function

The moment generating function is given by:

$M(t)=M\left(\frac{k}{2},\frac{1}{2},\frac{t^2}{2}\right)+$

$t\sqrt{2}\,\frac{\Gamma((k+1)/2)}{\Gamma(k/2)} M\left(\frac{k+1}{2},\frac{3}{2},\frac{t^2}{2}\right)$

Characteristic function

The characteristic function is given by:

$\varphi(t;k)=M\left(\frac{k}{2},\frac{1}{2},\frac{-t^2}{2}\right)+$

$it\sqrt{2}\,\frac{\Gamma((k+1)/2)}{\Gamma(k/2)} M\left(\frac{k+1}{2},\frac{3}{2},\frac{-t^2}{2}\right)$

where again, M(a,b,z) is Kummer's confluent hypergeometric function.

Properties

Moments

The raw moments are then given by:

$\mu_j=2^{j/2}\frac{\Gamma((k+j)/2)}{\Gamma(k/2)}$

where Γ(z) is the Gamma function. The first few raw moments are:

$\mu_1=\sqrt{2}\,\,\frac{\Gamma((k\!+\!1)/2)}{\Gamma(k/2)}$

$\mu_2=k\,$

$\mu_3=2\sqrt{2}\,\,\frac{\Gamma((k\!+\!3)/2)}{\Gamma(k/2)}=(k+1)\mu_1$

$\mu_4=(k)(k+2)\,$

$\mu_5=4\sqrt{2}\,\,\frac{\Gamma((k\!+\!5)/2)}{\Gamma(k/2)}=(k+1)(k+3)\mu_1$

$\mu_6=(k)(k+2)(k+4)\,$

where the rightmost expressions are derived using the recurrence relationship for the Gamma function:

$\Gamma(x+1)=x\Gamma(x)\,$

From these expressions we may derive the following relationships:

Mean: $\mu=\sqrt{2}\,\,\frac{\Gamma((k+1)/2)}{\Gamma(k/2)}$

Variance: $\sigma^2=k-\mu^2\,$

Skewness: $\gamma_1=\frac{\mu}{\sigma^3}\,(1-2\sigma^2)$

Kurtosis excess: $\gamma_2=\frac{2}{\sigma^2}(1-\mu\sigma\gamma_1-\sigma^2)$

Entropy

The entropy is given by:

$S=\ln(\Gamma(k/2))+\frac{1}{2}(k\!-\!\ln(2)\!-\!(k\!-\!1)\psi_0(k/2))$

where ψ₀(z) is the polygamma function.

Related distributions

• If X∼χ_k(x) then $X^2 \sim \chi^2_k$ (chi-squared distribution)
• $\lim_{k \to \infty}\tfrac{\chi_k(x)-\mu_k}{\sigma_k} \xrightarrow{d}\ N(0,1) \,$ (normal distribution)
• If $X \sim \chi_1(x) \,$ then $\sigma X \sim HN(\sigma)\,$ (half-normal distribution) for any $\sigma > 0 \,$
• $\chi_2(x) \sim \mathrm{Rayleigh}(1)\,$ (Rayleigh distribution)
• $\chi_3(x) \sim \mathrm{Maxwell}(1)\,$ (Maxwell distribution)
• $\|\boldsymbol{N}_{i=1,\ldots,k}{(0,1)}\| \sim \chi_k(x)$ (The norm of n standard normally distributed variables is a chi distribution with k degrees of freedom)
• chi distribution is a special case of the generalized gamma distribution

Various chi and chi-squared distributions

Name	Statistic
chi-squared distribution	$\sum_{i=1}^k \left(\frac{X_i-\mu_i}{\sigma_i}\right)^2$
noncentral chi-squared distribution	$\sum_{i=1}^k \left(\frac{X_i}{\sigma_i}\right)^2$
chi distribution	$\sqrt{\sum_{i=1}^k \left(\frac{X_i-\mu_i}{\sigma_i}\right)^2}$
noncentral chi distribution	$\sqrt{\sum_{i=1}^k \left(\frac{X_i}{\sigma_i}\right)^2}$

See also

• Nakagami distribution

External links

• http://mathworld.wolfram.com/ChiDistribution.html