Noncentral chi-squared distribution

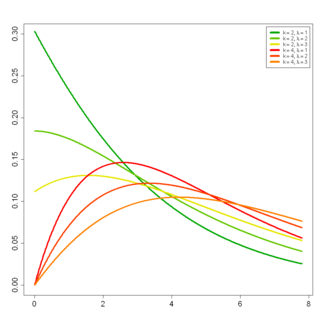
Noncentral chi-squared

Probability density function
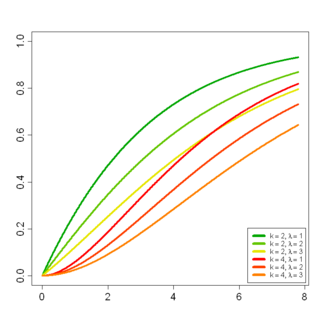
Cumulative distribution function
parameters:	$k > 0\,$ degrees of freedom $\lambda > 0\,$ non-centrality parameter
support:	$x \in [0; +\infty)\,$
pdf:	$\frac{1}{2}e^{-(x+\lambda)/2}\left (\frac{x}{\lambda} \right)^{k/4-1/2} I_{k/2-1}(\sqrt{\lambda x})$
cdf:	$1 - Q_{\frac{k}{2}} \left( \sqrt{\lambda}, \sqrt{x} \right)$ with Marcum Q-function QM(a,b)
mean:	$k+\lambda\,$
variance:	$2(k+2\lambda)\,$
skewness:	$\frac{2^{3/2}(k+3\lambda)}{(k+2\lambda)^{3/2}}$
ex.kurtosis:	$\frac{12(k+4\lambda)}{(k+2\lambda)^2}$
mgf:	$\frac{\exp\left(\frac{ \lambda t}{1-2t }\right)}{(1-2 t)^{k/2}}$ for 2t < 1
cf:	$\frac{\exp\left(\frac{i\lambda t}{1-2it}\right)}{(1-2it)^{k/2}}$

In probability theory and statistics, the noncentral chi-squared or noncentral χ² distribution is a generalization of the chi-squared distribution. This distribution often arises in the power analysis of statistical tests in which the null distribution is (perhaps asymptotically) a chi-squared distribution; important examples of such tests are the likelihood ratio tests.

Background

Let X_i be k independent, normally distributed random variables with means μ_i and variances $\sigma_i^2$. Then the random variable

$\sum_{i=1}^k \left(\frac{X_i}{\sigma_i}\right)^2$

is distributed according to the noncentral chi-squared distribution. It has two parameters: k which specifies the number of degrees of freedom (i.e. the number of X_i), and λ which is related to the mean of the random variables X_i by:

$\lambda=\sum_{i=1}^k \left(\frac{\mu_i}{\sigma_i}\right)^2.$

λ is sometime called the noncentrality parameter. Note that some references define λ in other ways, such as half of the above sum, or its square root.

This distribution arises in multivariate statistics as a derivative of the multivariate normal distribution. While the central chi-squared distribution is the squared norm of a random vector with N(0_k,I_k) distribution (i.e., the squared distance from the origin of a point taken at random from that distribution), the non-central χ² is the squared norm of a random vector with N(μ,I_k) distribution. Here 0_k is a zero vector of length k, μ = (μ₁,...,μ_k) and I_k is the identity matrix of size k.

Properties

Probability density function

The probability density function is given by

$f_X(x; k,\lambda) = \sum_{i=0}^\infty \frac{e^{-\lambda/2} (\lambda/2)^i}{i!} f_{Y_{k+2i}}(x),$

where Y_q is distributed as chi-squared with q degrees of freedom.

From this representation, the noncentral chi-squared distribution is seen to be a Poisson-weighted mixture of central chi-squared distributions. Suppose that a random variable J has a Poisson distribution with mean λ / 2, and the conditional distribution of Z given J = i is chi-squared with k+2i degrees of freedom. Then the unconditional distribution of Z is non-central chi-squared with k degrees of freedom, and non-centrality parameter λ.

Alternatively, the pdf can be written as

$f_X(x;k,\lambda)=\frac{1}{2} e^{-(x+\lambda)/2} \left (\frac{x}{\lambda}\right)^{k/4-1/2} I_{k/2-1}(\sqrt{\lambda x})$

where I_ν(z) is a modified Bessel function of the first kind given by

$I_a(y) = (y/2)^a \sum_{j=0}^\infty \frac{ (y^2/4)^j}{j! \Gamma(a+j+1)} .$

Using the relation between Bessel functions and hypergeometric functions, the pdf can also be written as:^[1]

$f_X(x;k,\lambda)={{\rm e}^{-\lambda/2}} _0F_1(;k/2;\lambda x/4)\frac{1}{2^{k/2}\Gamma(k/2)} {\rm e}^{-x/2} x^{k/2-1}.$

Siegel (1979) discusses the case k=0 specifically (zero degrees of freedom), in which case the distribution has a discrete component at zero.

Moment generating function

The moment generating function is given by

$M(t;k,\lambda)=\frac{\exp\left(\frac{ \lambda t}{1-2t }\right)}{(1-2 t)^{k/2}}.$

The first few raw moments are:

$\mu^'_1=k+\lambda$

$\mu^'_2=(k+\lambda)^2 + 2(k + 2\lambda)$

$\mu^'_3=(k+\lambda)^3 + 6(k+\lambda)(k+2\lambda)+8(k+3\lambda)$

$\mu^'_4=(k+\lambda)^4+12(k+\lambda)^2(k+2\lambda)+4(11k^2+44k\lambda+36\lambda^2)+48(k+4\lambda)$

The first few central moments are:

$\mu_2=2(k+2\lambda)\,$

$\mu_3=8(k+3\lambda)\,$

$\mu_4=12(k+2\lambda)^2+48(k+4\lambda)\,$

The nth cumulant is

$K_n=2^{n-1}(n-1)!(k+n\lambda).\,$

Hence

$\mu^'_n = 2^{n-1}(n-1)!(k+n\lambda)+\sum_{j=1}^{n-1} \frac{(n-1)!2^{j-1}}{(n-j)!}(k+j\lambda )\mu^'_{n-j}.$

Cumulative distribution function

Again using the relation between the central and noncentral chi-squared distributions, the cumulative distribution function (cdf) can be written as

$P(x; k, \lambda ) = e^{-\lambda/2}\; \sum_{j=0}^\infty \frac{(\lambda/2)^j}{j!} Q(x; k+2j)$

where $Q(x; k)\,$ is the cumulative distribution function of the central chi-squared distribution which is given by

$Q(x;k)=\frac{\gamma(k/2,x/2)}{\Gamma(k/2)}\,$

and where $\gamma(k,z)\,$ is the lower incomplete Gamma function.

The Marcum Q-function Q_M(a,b)can also be used to represent the cdf.^[2]

$P(x; k, \lambda) = 1 - Q_{\frac{k}{2}} \left( \sqrt{\lambda}, \sqrt{x} \right)$

Approximation

Sankaran ^[3] discusses a number of closed form approximations for the cumulative distribution function. In an earlier paper,^[4] he derived and states the following approximation:

$P(x; k, \lambda ) \approx \Phi \lbrace \frac{(\frac{x} {k + \lambda}) ^ h - (1 + h p (h - 1 - 0.5 (2 - h) m p))} {h \sqrt{ 2p} (1 + 0.5 m p)} \rbrace$

where

$\Phi \lbrace \cdot \rbrace \,$ denotes the cumulative distribution function of the standard normal distribution;

$h = 1 - \frac{2}{3} \frac{(k+ \lambda) (k+ 3 \lambda)}{(k+ 2 \lambda) ^ 2} \, ;$

$p = \frac{k+ 2 \lambda}{(k+ \lambda) ^ 2} ;$

$m = (h - 1) (1 - 3 h) \, .$

This and other approximations are discussed in a later text book.^[5]

To approximate the Chi-squared distribution, the non-centrality parameter, $\lambda\,$, is set to zero.

For a given probability, the formula is easily inverted to provide the corresponding approximation for $x\,$.

Derivation of the pdf

The derivation of the probability density function is most easily done by performing the following steps:

1. First, assume without loss of generality that $\sigma_1=\ldots=\sigma_k=1$. Then the joint distribution of $X_1,\ldots,X_k$ is spherically symmetric, up to a location shift.
2. The spherical symmetry then implies that the distribution of $X=X_1^2+\ldots+X_k^2$ depends on the means only through the squared length, $\lambda=\mu_1^2+\ldots+\mu_k^2$. Without loss of generality, we can therefore take $\mu_1=\sqrt{\lambda}$ and $\mu_2=\dots=\mu_k=0$.
3. Now derive the density of $X=X_1^2$ (i.e. k=1 case). Simple transformation of random variables shows that :$\begin{align}f_X(x,1,\lambda) &= \frac{1}{2\sqrt{x}}\left( \phi(\sqrt{x}-\sqrt{\lambda}) + \phi(\sqrt{x}+\sqrt{\lambda}) \right )\\ &= \frac{1}{\sqrt{2\pi x}} e^{-(x+\lambda)/2} \cosh(\sqrt{\lambda x}),\\ \end{align}$
   where $\phi(\cdot)$ is the standard normal density.
4. Expand the cosh term in a Taylor series. This gives the Poisson-weighted mixture representation of the density, still for k=1. The indices on the chi-squared random variables in the series above are 1+2i in this case.
5. Finally, for the general case. We've assumed, without loss of generality, that $X_2,\ldots,X_k$ are standard normal, and so $X_2^2+\ldots+X_k^2$ has a central chi-squared distribution with (k-1) degrees of freedom, independent of $X_1^2$. Using the poisson-weighted mixture representation for $X_1^2$, and the fact that the sum of chi-squared random variables is also chi-squared, completes the result. The indices in the series are (1+2i)+(k-1) = k+2i as required.

Related distributions

• If V is chi-squared distributed $V \sim \chi_k^2$ then V is also non-central chi-squared distributed: $V \sim {\chi'}^2_k(0)$

• If $V_1 \sim {\chi'}_{k_1}^2(\lambda)$ and $V_2 \sim {\chi'}_{k_2}^2(0)$ and V₁ is independent of V₂ then a noncentral F-distributed variable is developed as $\frac{V_1/k_1}{V_2/k_2} \sim F'_{k_1,k_2}(\lambda)$

• If $J \sim Poisson(\frac{\lambda}{2})$, then $\chi_{k+2J}^2 \sim {\chi'}_k^2(\lambda)$

• Normal approximation^[6]: if $V \sim {\chi'}^2_k(\lambda)$, then $\frac{V-(k+\lambda)}{\sqrt{2(k+2\lambda)}}\to N(0,1)$ in distribution as either $k\to\infty$ or $\lambda\to\infty$.

Transformations

Sankaran (1963) discusses the transformations of the form z = [(X − b) / (k + λ)]^{1 / 2}. He analyzes the expansions of the cumulants of z up to the term O((k + λ) ^{− 4}) and shows that the following choices of b produce reasonable results:

• b = (k − 1) / 2 makes the second cumulant of z approximately independent of λ

• b = (k − 1) / 3 makes the third cumulant of z approximately independent of λ

• b = (k − 1) / 4 makes the fourth cumulant of z approximately independent of λ

Also, a simpler transformation z₁ = (X − (k − 1) / 2)^{1 / 2} can be used as a variance stabilizing transformation that produces a random variable with mean (λ + (k − 1) / 2)^{1 / 2} and variance O((k + λ) ^{− 2}).

Usability of these transformations may be hampered by the need to take the square roots of negative numbers.

Various chi and chi-squared distributions

Name	Statistic
chi-squared distribution	$\sum_1^k \left(\frac{X_i-\mu_i}{\sigma_i}\right)^2$
noncentral chi-squared distribution	$\sum_1^k \left(\frac{X_i}{\sigma_i}\right)^2$
chi distribution	$\sqrt{\sum_1^k \left(\frac{X_i-\mu_i}{\sigma_i}\right)^2}$
noncentral chi distribution	$\sqrt{\sum_1^k \left(\frac{X_i}{\sigma_i}\right)^2}$

Notes

1. ^ Muirhead (2005) Theorem 1.3.4
2. ^ Nuttall, Albert H. (1975): Some Integrals Involving the Q_M Function, IEEE Transactions on Information Theory, 21(1), 95-96, ISSN 0018-9448
3. ^ Sankaran , M. (1963). Approximations to the non-central chi-squared distribution Biometrika, 50(1-2), 199–204
4. ^ Sankaran , M. (1959). "On the non-central chi-squared distribution", Biometrika 46, 235–237
5. ^ Johnson et al. (1995) Section 29.8
6. ^ Muirhead (2005) pages 22–24 and problem 1.18.

References

• Abramowitz, M. and Stegun, I.A. (1972), Handbook of Mathematical Functions, Dover. Section 26.4.25.
• Johnson, N. L., Kotz, S., Balakrishnan, N. (1970), Continuous Univariate Distributions, Volume 2, Wiley. ISBN 0-471-58494-0
• Muirhead, R. (2005) Aspects of Multivariate Statistical Theory, Wiley
• Siegel, A.F. (1979), "The noncentral chi-squared distribution with zero degrees of freedom and testing for uniformity", Biometrika, 66, 381–386
• Press, S.J. (1966), "Linear combinations of non-central chi-squared variates", The Annals of Mathematical Statistics 37 (2): 480–487, JSTOR 2238621