- Nuclear fission
-
"Splitting the atom" redirects here. For the EP, see Splitting the Atom.
Nuclear physics Radioactive decay
Nuclear fission
Nuclear fusionClassical decaysAdvanced decaysEmission processesCapturingHigh energy processesIn nuclear physics and nuclear chemistry, nuclear fission is a nuclear reaction in which the nucleus of an atom splits into smaller parts (lighter nuclei), often producing free neutrons and photons (in the form of gamma rays), and releasing a tremendous amount of energy. The two nuclei produced are most often of comparable size, typically with a mass ratio around 3:2 for common fissile isotopes.[1][2] Most fissions are binary fissions, but occasionally (2 to 4 times per 1000 events), three positively charged fragments are produced in a ternary fission. The smallest of these ranges in size from a proton to an argon nucleus.
Fission is usually an energetic nuclear reaction induced by a neutron, although it is occasionally seen as a form of spontaneous radioactive decay, especially in very high-mass-number isotopes. The unpredictable composition of the products (which vary in a broad probabilistic and somewhat chaotic manner) distinguishes fission from purely quantum-tunnelling processes such as proton emission, alpha decay and cluster decay, which give the same products every time.
Fission of heavy elements is an exothermic reaction which can release large amounts of energy both as electromagnetic radiation and as kinetic energy of the fragments (heating the bulk material where fission takes place). In order for fission to produce energy, the total binding energy of the resulting elements must be greater than that of the starting element. Fission is a form of nuclear transmutation because the resulting fragments are not the same element as the original atom.
Nuclear fission produces energy for nuclear power and to drive the explosion of nuclear weapons. Both uses are possible because certain substances called nuclear fuels undergo fission when struck by fission neutrons, and in turn emit neutrons when they break apart. This makes possible a self-sustaining chain reaction that releases energy at a controlled rate in a nuclear reactor or at a very rapid uncontrolled rate in a nuclear weapon.
The amount of free energy contained in nuclear fuel is millions of times the amount of free energy contained in a similar mass of chemical fuel such as gasoline, making nuclear fission a very dense source of energy. The products of nuclear fission, however, are on average far more radioactive than the heavy elements which are normally fissioned as fuel, and remain so for significant amounts of time, giving rise to a nuclear waste problem. Concerns over nuclear waste accumulation and over the destructive potential of nuclear weapons may counterbalance the desirable qualities of fission as an energy source, and give rise to ongoing political debate over nuclear power.
Contents
Physical overview
Mechanics
 A visual representation of an induced nuclear fission event where a slow-moving neutron is absorbed by the nucleus of a uranium-235 atom, which fissions into two fast-moving lighter elements (fission products) and additional neutrons. Most of the energy released is in the form of the kinetic velocities of the fission products and the neutrons. Also shown is the capture of a neutron by uranium-238 to become uranium-239.
A visual representation of an induced nuclear fission event where a slow-moving neutron is absorbed by the nucleus of a uranium-235 atom, which fissions into two fast-moving lighter elements (fission products) and additional neutrons. Most of the energy released is in the form of the kinetic velocities of the fission products and the neutrons. Also shown is the capture of a neutron by uranium-238 to become uranium-239.
Nuclear fission can occur without neutron bombardment, as a type of radioactive decay. This type of fission (called spontaneous fission) is rare except in a few heavy isotopes. In engineered nuclear devices, essentially all nuclear fission occurs as a "nuclear reaction" — a bombardment-driven process that results from the collision of two subatomic particles. In nuclear reactions, a subatomic particle collides with an atomic nucleus and causes changes to it. Nuclear reactions are thus driven by the mechanics of bombardment, not by the relatively constant exponential decay and half-life characteristic of spontaneous radioactive processes.
Many types of nuclear reactions are currently known. Nuclear fission differs importantly from other types of nuclear reactions, in that it can be amplified and sometimes controlled via a nuclear chain reaction. In such a reaction, free neutrons released by each fission event can trigger yet more events, which in turn release more neutrons and cause more fissions.
The chemical element isotopes that can sustain a fission chain reaction are called nuclear fuels, and are said to be fissile. The most common nuclear fuels are 235U (the isotope of uranium with an atomic mass of 235 and of use in nuclear reactors) and 239Pu (the isotope of plutonium with an atomic mass of 239). These fuels break apart into a bimodal range of chemical elements with atomic masses centering near 95 and 135 u (fission products). Most nuclear fuels undergo spontaneous fission only very slowly, decaying instead mainly via an alpha/beta decay chain over periods of millennia to eons. In a nuclear reactor or nuclear weapon, the overwhelming majority of fission events are induced by bombardment with another particle, a neutron, which is itself produced by prior fission events.
Nuclear fissions in fissile fuels are the result of the nuclear excitation energy produced when a fissile nucleus captures a neutron. This energy, resulting from the neutron capture, is a result of the attractive nuclear force acting between the neutron and nucleus. It is enough to deform the nucleus into a double-lobed "drop," to the point that nuclear fragments exceed the distances at which the nuclear force can hold two groups of charged nucleons together, and when this happens, the two fragments complete their separation and then are driven further apart by their mutually repulsive charges, in a process which becomes irreversible with greater and greater distance. A similar process occurs in fissionable isotopes (such as uranium-238), but in order to fission, these isotopes require additional energy provided by fast neutrons (such as produced by nuclear fusion in thermonuclear weapons).
The liquid drop model of the atomic nucleus predicts equal-sized fission products as a mechanical outcome of nuclear deformation. The more sophisticated nuclear shell model is needed to mechanistically explain the route to the more energetically favorable outcome, in which one fission product is slightly smaller than the other.
The most common fission process is binary fission, and it produces the fission products noted above, at 95±15 and 135±15 u. However, the binary process happens merely because it is the most probable. In anywhere from 2 to 4 fissions per 1000 in a nuclear reactor, a process called ternary fission produces three positively charged fragments (plus neutrons) and the smallest of these may range from so small a charge and mass as a proton (Z=1), to as large a fragment as argon (Z=18). The most common small fragments, however, are composed of 90% helium-4 nuclei with more energy than alpha particles from alpha decay (so-called "long range alphas" at ~ 16 MeV), plus helium-6 nuclei, and tritons (the nuclei of tritium). The ternary process is less common, but still ends up producing significant helium-4 and tritium gas buildup in the fuel rods of modern nuclear reactors.[3]
Energetics
Input
 The stages of binary fission in a liquid drop model. Energy input deforms the nucleus into a fat "cigar" shape, then a "peanut" shape, followed by binary fission as the two lobes exceed the short-range strong force attraction distance, then are pushed apart and away by their electrical charge. Note that in this model, the two fission fragments are the same size.
The stages of binary fission in a liquid drop model. Energy input deforms the nucleus into a fat "cigar" shape, then a "peanut" shape, followed by binary fission as the two lobes exceed the short-range strong force attraction distance, then are pushed apart and away by their electrical charge. Note that in this model, the two fission fragments are the same size.
The fission of a heavy nucleus requires a total input energy of about 7 to 8 MeV to initially overcome the strong force which holds the nucleus into a spherical or nearly spherical shape, and from there, deform it into a two-lobed ("peanut") shape in which the lobes are able to continue to separate from each other, pushed by their mutual positive charge, in the most common process of binary fission (two positively charged fission products + neutrons). Once the nuclear lobes have been pushed to a critical distance, beyond which the short range strong force can no longer hold them together, the process of their separation proceeds from the energy of the (longer range) electromagnetic repulsion between the fragments. The result is two fission fragments moving away from each other, at high energy.
About 6 MeV of the fission-input energy is supplied by the simple binding of the neutron to the nucleus via the strong force— however in many fissionable isotopes, this amount of energy is not enough for fission. If no additional energy is supplied by any other mechanism, the nucleus will not fission, but will merely absorb the neutron, as happens when U-238 absorbs slow neutrons to become U-239. The remaining energy to initiate fission can be supplied by two other mechanisms: one of these is the kinetic energy of the incoming neutron, which is increasingly able to fission a fissionable heavy nucleus as it exceeds a kinetic energy of one MeV or more (so-called fast neutrons). Such high energy neutrons are able to fission U-238 directly (see thermonuclear weapon for application, where the fast neutrons are supplied by nuclear fusion). However, this process cannot happen to a great extent in a nuclear reactor, as too small a fraction of the fission neutrons produced by any type of fission have enough energy to directly fission U-238.
Among the heavy actinide elements, however, those isotopes that have an odd number of neutrons bind neutrons with an additional 1 to 2 MeV of energy, which is made available as a result of the mechanism of neutron pairing effects. This extra energy results from the Pauli exclusion principle allowing an extra neutron to occupy the same nuclear orbital as the last neutron in the nucleus, so that the two form a pair. In such isotopes, therefore, no neutron kinetic energy is needed, for all the necessary energy is supplied by absorption of any neutron, either of the slow or fast variety (the former are used in nuclear reactors, and the latter are used in weapons). As noted above, the subgroup of fissionable elements that may be fissioned with their own fission neutrons, are termed fissile. Examples of fissile isotopes are U-235 and plutonium-239.
Output
Typical fission events release about two hundred million eV (200 MeV) of energy for each fission event. By contrast, most chemical oxidation reactions (such as burning coal or TNT) release at most a few eV per event. So, nuclear fuel contains at least ten million times more usable energy per unit mass than does chemical fuel. The energy of nuclear fission is released as kinetic energy of the fission products and fragments, and as electromagnetic radiation in the form of gamma rays; in a nuclear reactor, the energy is converted to heat as the particles and gamma rays collide with the atoms that make up the reactor and its working fluid, usually water or occasionally heavy water.
When a uranium nucleus fissions into two daughter nuclei fragments, about one-tenth of 1 percent of the mass of the uranium nucleus[4] is converted to energy of ~200 MeV. For uranium-235 (total mean fission energy 202.5 MeV), typically ~169 MeV appears as the kinetic energy of the daughter nuclei, which fly apart at about 3% of the speed of light, due to Coulomb repulsion. Also, an average of 2.5 neutrons are emitted with a kinetic energy of ~2 MeV each (total of 4.8 MeV). The fission reaction also releases ~7 MeV in prompt gamma ray photons. The latter figure means that a nuclear fission explosion or criticality accident emits about 3.5% of its energy as gamma rays, less than 2.5% of its energy as fast neutrons (total ~ 6%), and the rest as kinetic energy of fission fragments ("heat"). In an atomic bomb, this heat may serve to raise the temperature of the bomb core to 100 million kelvin and cause secondary emission of soft X-rays, which convert some of this energy to ionizing radiation. However, in nuclear generators, the fission fragment kinetic energy remains as low-temperature heat which causes little or no ionization.
So-called neutron bombs (enhanced radiation weapons) have been constructed which release a larger fraction of their energy as ionizing radiation (specifically, neutrons), but these are all thermonuclear devices which rely on the nuclear fusion stage to produce the extra radiation. The energy dynamics of pure fission bombs always remain at about 6% yield of the total in radiation, as a prompt result of fission.
The total prompt fission energy amounts to about 181 MeV, or ~ 89% of the total energy which is eventually released by fission over time. The remaining ~ 11% is released in beta decays which have various half-lives, but begin as a process in the fission products immediately; and in delayed gamma emissions associated with these beta decays. For example, in uranium-235 this delayed energy is divided into about 6.5 MeV in betas, 8.8 MeV in antineutrinos (released at the same time as the betas), and finally, an additional 6.3 MeV in delayed gamma emission from the excited beta-decay products (for a mean total of ~10 gamma ray emissions per fission, in all). Thus, an additional 6% of the total energy of fission is also released eventually as non-prompt ionizing radiation, and this is about evenly divided between gamma and beta ray energy. The remainder is antineutrinos.
The 8.8 MeV/202.5 MeV = 4.3% of the energy which is released as antineutrinos is not captured by the reactor material as heat, and escapes directly through all materials (including the Earth) at nearly the speed of light, and into interplanetary space (the amount absorbed is miniscule). Neutrino radiation is ordinarily not classed as ionizing radiation, because it is not absorbed and therefore does not produce effects. Almost all of the rest of the radiation (beta and gamma radiation) is eventually converted to heat in a reactor core or its shielding.
Some processes involving neutrons are notable for absorbing or finally yielding energy — for example neutron kinetic energy does not yield heat immediately if the neutron is captured by a uranium-238 atom to breed plutonium-239, but this energy is emitted if the plutonium-239 is later fissioned. On the other hand, so-called delayed neutrons emitted as radioactive decay products with half-lives up to several minutes, from fission-daughters, are very important to reactor control, because they give a characteristic "reaction" time for the total nuclear reaction to double in size, if the reaction is run in a "delayed-critical" zone which deliberately relies on these neutrons for a supercritical chain-reaction (one in which each fission cycle yields more neutrons than it absorbs). Without their existence, the nuclear chain-reaction would be prompt critical and increase in size faster than it could be controlled by human intervention. In this case, the first experimental atomic reactors would have run away to a dangerous and messy "prompt critical reaction" before their operators could have manually shut them down (for this reason, designer Enrico Fermi included radiation-counter-triggered control rods, suspended by electromagnets, which could automatically drop into the center of Chicago Pile-1). If these delayed neutrons are captured without producing fissions, they produce heat as well.[5]
Product nuclei and binding energy
In fission there is a preference to yield fragments with even proton numbers, which is called the odd-even effect on the fragments charge distribution. However, no odd-even effect is observed on fragment mass number distribution. This result is attributed to nucleon pair breaking.
In nuclear fission events the nuclei may break into any combination of lighter nuclei, but the most common event is not fission to equal mass nuclei of about mass 120; the most common event (depending on isotope and process) is a slightly unequal fission in which one daughter nucleus has a mass of about 90 to 100 u and the other the remaining 130 to 140 u.[6] Unequal fissions are energetically more favorable because this allows one product to be closer to the energetic minimum near mass 60 u (only a quarter of the average fissionable mass), while the other nucleus with mass 135 u is still not far out of the range of the most tightly bound nuclei (another statement of this, is that the atomic binding energy curve is slightly steeper to the left of mass 120 u than to the right of it).
Origin of the active energy and the curve of binding energy
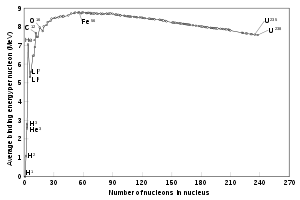
Nuclear fission of heavy elements produces energy because the specific binding energy (binding energy per mass) of intermediate-mass nuclei with atomic numbers and atomic masses close to 62Ni and 56Fe is greater than the nucleon-specific binding energy of very heavy nuclei, so that energy is released when heavy nuclei are broken apart. The total rest masses of the fission products (Mp) from a single reaction is less than the mass of the original fuel nucleus (M). The excess mass Δm = M – Mp is the invariant mass of the energy that is released as photons (gamma rays) and kinetic energy of the fission fragments, according to the mass-energy equivalence formula E = mc2.
The variation in specific binding energy with atomic number is due to the interplay of the two fundamental forces acting on the component nucleons (protons and neutrons) that make up the nucleus. Nuclei are bound by an attractive nuclear force between nucleons, which overcomes the electrostatic repulsion between protons. However, the nuclear force acts only over relatively short ranges (a few nucleon diameters), since it follows an exponentially decaying Yukawa potential which makes it insignificant at longer distances. The electrostatic repulsion is of longer range, since it decays by an inverse-square rule, so that nuclei larger than about 12 nucleons in diameter reach a point that the total electrostatic repulsion overcomes the nuclear force and causes them to be spontaneously unstable. For the same reason, larger nuclei (more than about eight nucleons in diameter) are less tightly bound per unit mass than are smaller nuclei; breaking a large nucleus into two or more intermediate-sized nuclei, releases energy. The origin of this energy is the nuclear force, which intermediate-sized nuclei allows to act more efficiently, because each nucleon has more neighbors which are within the short range attraction of this force. Thus less energy is needed in the smaller nuclei and the difference to the state before is set free.
Also because of the short range of the strong binding force, large stable nuclei must contain proportionally more neutrons than do the lightest elements, which are most stable with a 1 to 1 ratio of protons and neutrons. Nuclei which have more than 20 protons cannot be stable unless they have more than an equal number of neutrons. Extra neutrons stabilize heavy elements because they add to strong-force binding (which acts between all nucleons), without adding to proton–proton repulsion. Fission products have, on average, about the same ratio of neutrons and protons as their parent nucleus, and are therefore usually unstable to beta decay (which changes neutrons to protons) because they have proportionally too many neutrons compared to stable isotopes of similar mass.
This tendency for fission product nuclei to beta-decay is the fundamental cause of the problem of radioactive high level waste from nuclear reactors. Fission products tend to be beta emitters, emitting fast-moving electrons to conserve electric charge, as excess neutrons convert to protons in the fission-product atoms. See Fission products (by element) for a description of fission products sorted by element.
Chain reactions
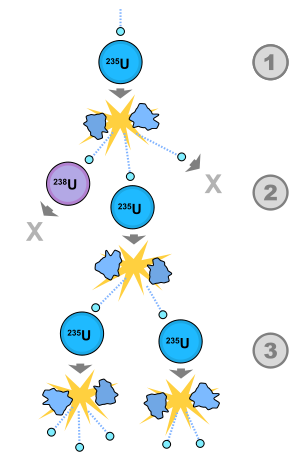 A schematic nuclear fission chain reaction. 1. A uranium-235 atom absorbs a neutron and fissions into two new atoms (fission fragments), releasing three new neutrons and some binding energy. 2. One of those neutrons is absorbed by an atom of uranium-238 and does not continue the reaction. Another neutron is simply lost and does not collide with anything, also not continuing the reaction. However one neutron does collide with an atom of uranium-235, which then fissions and releases two neutrons and some binding energy. 3. Both of those neutrons collide with uranium-235 atoms, each of which fissions and releases between one and three neutrons, which can then continue the reaction.
A schematic nuclear fission chain reaction. 1. A uranium-235 atom absorbs a neutron and fissions into two new atoms (fission fragments), releasing three new neutrons and some binding energy. 2. One of those neutrons is absorbed by an atom of uranium-238 and does not continue the reaction. Another neutron is simply lost and does not collide with anything, also not continuing the reaction. However one neutron does collide with an atom of uranium-235, which then fissions and releases two neutrons and some binding energy. 3. Both of those neutrons collide with uranium-235 atoms, each of which fissions and releases between one and three neutrons, which can then continue the reaction.
Several heavy elements, such as uranium, thorium, and plutonium, undergo both spontaneous fission, a form of radioactive decay and induced fission, a form of nuclear reaction. Elemental isotopes that undergo induced fission when struck by a free neutron are called fissionable; isotopes that undergo fission when struck by a thermal, slow moving neutron are also called fissile. A few particularly fissile and readily obtainable isotopes (notably 235U and 239Pu) are called nuclear fuels because they can sustain a chain reaction and can be obtained in large enough quantities to be useful.
All fissionable and fissile isotopes undergo a small amount of spontaneous fission which releases a few free neutrons into any sample of nuclear fuel. Such neutrons would escape rapidly from the fuel and become a free neutron, with a mean lifetime of about 15 minutes before decaying to protons and beta particles. However, neutrons almost invariably impact and are absorbed by other nuclei in the vicinity long before this happens (newly created fission neutrons move at about 7% of the speed of light, and even moderated neutrons move at about 8 times the speed of sound). Some neutrons will impact fuel nuclei and induce further fissions, releasing yet more neutrons. If enough nuclear fuel is assembled in one place, or if the escaping neutrons are sufficiently contained, then these freshly emitted neutrons outnumber the neutrons that escape from the assembly, and a sustained nuclear chain reaction will take place.
An assembly that supports a sustained nuclear chain reaction is called a critical assembly or, if the assembly is almost entirely made of a nuclear fuel, a critical mass. The word "critical" refers to a cusp in the behavior of the differential equation that governs the number of free neutrons present in the fuel: if less than a critical mass is present, then the amount of neutrons is determined by radioactive decay, but if a critical mass or more is present, then the amount of neutrons is controlled instead by the physics of the chain reaction. The actual mass of a critical mass of nuclear fuel depends strongly on the geometry and surrounding materials.
Not all fissionable isotopes can sustain a chain reaction. For example, 238U, the most abundant form of uranium, is fissionable but not fissile: it undergoes induced fission when impacted by an energetic neutron with over 1 MeV of kinetic energy. But too few of the neutrons produced by 238U fission are energetic enough to induce further fissions in 238U, so no chain reaction is possible with this isotope. Instead, bombarding 238U with slow neutrons causes it to absorb them (becoming 239U) and decay by beta emission to 239Np which then decays again by the same process to 239Pu; that process is used to manufacture 239Pu in breeder reactors. In-situ plutonium production also contributes to the neutron chain reaction in other types of reactors after sufficient plutonium-239 has been produced, since plutonium-239 is also a fissile element which serves as fuel. It is estimated that up to half of the power produced by a standard "non-breeder" reactor is produced by the fission of plutonium-239 produced in place, over the total life-cycle of a fuel load.
Fissionable, non-fissile isotopes can be used as fission energy source even without a chain reaction. Bombarding 238U with fast neutrons induces fissions, releasing energy as long as the external neutron source is present. This is an important effect in all reactors where fast neutrons from the fissile isotope can cause the fission of nearby 238U nuclei, which means that some small part of the 238U is "burned-up" in all nuclear fuels, especially in fast breeder reactors that operate with higher-energy neutrons. That same fast-fission effect is used to augment the energy released by modern thermonuclear weapons, by jacketing the weapon with 238U to react with neutrons released by nuclear fusion at the center of the device.
Fission reactors
Critical fission reactors are the most common type of nuclear reactor. In a critical fission reactor, neutrons produced by fission of fuel atoms are used to induce yet more fissions, to sustain a controllable amount of energy release. Devices that produce engineered but non-self-sustaining fission reactions are subcritical fission reactors. Such devices use radioactive decay or particle accelerators to trigger fissions.
Critical fission reactors are built for three primary purposes, which typically involve different engineering trade-offs to take advantage of either the heat or the neutrons produced by the fission chain reaction:
- power reactors are intended to produce heat for nuclear power, either as part of a generating station or a local power system such as a nuclear submarine.
- research reactors are intended to produce neutrons and/or activate radioactive sources for scientific, medical, engineering, or other research purposes.
- breeder reactors are intended to produce nuclear fuels in bulk from more abundant isotopes. The better known fast breeder reactor makes 239Pu (a nuclear fuel) from the naturally very abundant 238U (not a nuclear fuel). Thermal breeder reactors previously tested using 232Th to breed the fissile isotope 233U continue to be studied and developed.
While, in principle, all fission reactors can act in all three capacities, in practice the tasks lead to conflicting engineering goals and most reactors have been built with only one of the above tasks in mind. (There are several early counter-examples, such as the Hanford N reactor, now decommissioned). Power reactors generally convert the kinetic energy of fission products into heat, which is used to heat a working fluid and drive a heat engine that generates mechanical or electrical power. The working fluid is usually water with a steam turbine, but some designs use other materials such as gaseous helium. Such reactors often give off radioactive waste that is especially hard to safely dispose, since it must be stored in radioactive proof locations, such as underground. Research reactors produce neutrons that are used in various ways, with the heat of fission being treated as an unavoidable waste product. Breeder reactors are a specialized form of research reactor, with the caveat that the sample being irradiated is usually the fuel itself, a mixture of 238U and 235U. For a more detailed description of the physics and operating principles of critical fission reactors, see nuclear reactor physics. For a description of their social, political, and environmental aspects, see nuclear power.
Fission bombs
 The mushroom cloud of the atom bomb dropped on Nagasaki, Japan in 1945 rose some 18 kilometres (11 mi) above the bomb's hypocenter. The bomb killed at least 60,000 people.[7]
The mushroom cloud of the atom bomb dropped on Nagasaki, Japan in 1945 rose some 18 kilometres (11 mi) above the bomb's hypocenter. The bomb killed at least 60,000 people.[7]
One class of nuclear weapon, a fission bomb (not to be confused with the fusion bomb), otherwise known as an atomic bomb or atom bomb, is a fission reactor designed to liberate as much energy as possible as rapidly as possible, before the released energy causes the reactor to explode (and the chain reaction to stop). Development of nuclear weapons was the motivation behind early research into nuclear fission: the Manhattan Project of the U.S. military during World War II carried out most of the early scientific work on fission chain reactions, culminating in the Trinity test bomb and the Little Boy and Fat Man bombs that were exploded over the cities Hiroshima, and Nagasaki, Japan in August 1945.
Even the first fission bombs were thousands of times more explosive than a comparable mass of chemical explosive. For example, Little Boy weighed a total of about four tons (of which 60 kg was nuclear fuel) and was 11 feet (3.4 m) long; it also yielded an explosion equivalent to about 15 kilotons of TNT, destroying a large part of the city of Hiroshima. Modern nuclear weapons (which include a thermonuclear fusion as well as one or more fission stages) are literally hundreds of times more energetic for their weight than the first pure fission atomic bombs, so that a modern single missile warhead bomb weighing less than 1/8 as much as Little Boy (see for example W88) has a yield of 475,000 tons of TNT, and could bring destruction to 10 times the city area.
While the fundamental physics of the fission chain reaction in a nuclear weapon is similar to the physics of a controlled nuclear reactor, the two types of device must be engineered quite differently (see nuclear reactor physics). A nuclear bomb is designed to release all its energy at once, while a reactor is designed to generate a steady supply of useful power. While overheating of a reactor can lead to, and has led to, meltdown and steam explosions, the much lower uranium enrichment makes it impossible for a nuclear reactor to explode with the same destructive power as a nuclear weapon. It is also difficult to extract useful power from a nuclear bomb, although at least one rocket propulsion system, Project Orion, is intended to work by exploding fission bombs behind a massively padded and shielded vehicle.
The strategic importance of nuclear weapons is a major reason why the technology of nuclear fission is politically sensitive. Viable fission bomb designs are, arguably, within the capabilities of many being relatively simple from an engineering viewpoint. However, the difficulty of obtaining fissile nuclear material to realize the designs, is the key to the relative unavailability of nuclear weapons to all but modern industrialized governments with special programs to produce fissile materials (see uranium enrichment and nuclear fuel cycle).
History
Discovery of fission
The discovery of nuclear fission occurred in 1938, following nearly five decades of work on the science of radioactivity and the elaboration of new nuclear physics that described the components of atoms. In 1911, New Zealander Lord Ernest Rutherford proposed a model of the atom in which a very small, dense and positively charged nucleus of protons was surrounded by orbiting, negatively charged electrons (the Rutherford model).[8] Niels Bohr improved upon this in 1913 by reconciling the quantum behavior of electrons (the Bohr model). Work by Henri Becquerel, Marie Curie, Pierre Curie, and Rutherford further elaborated that the nucleus, though tightly bound, could undergo different forms of radioactive decay, and thereby transmute into other elements (for example, by losing an alpha particle). All known radioactive processes before fission changed mass of the atomic nucleus by no more than two protons and two neutrons (Alpha decay). Albert Einstein's principle of mass–energy equivalence described the amount of energy released in such processes, but this could not be harnessed on a large scale.
Some work in nuclear transmutation had been done. In 1917, Rutherford was able to accomplish transmutation of nitrogen into oxygen, using alpha particles directed at nitrogen 14N + α → 17O + p. This was the first observation of a nuclear reaction, that is, a reaction in which particles from one decay are used to transform another atomic nucleus. Eventually, in 1932, a fully artificial nuclear reaction and nuclear transmutation was achieved by Rutherford's colleagues John Cockcroft and Ernest Walton, who used artificially accelerated protons against lithium-7, to split this nucleus into two alpha particles. The feat was popularly known as splitting the atom, although it was not the modern nuclear fission reaction later discovered in heavy elements, which is discussed below.[9] Meanwhile, the possibility of combining two light nuclei in nuclear fusion had been studied in connection with the processes which power stars, and the first nuclear fusion reaction had been produced using accelerated deuterium nuclei, by Mark Oliphant, in 1932.
After English physicist James Chadwick discovered the neutron in 1932,[10] Enrico Fermi and his colleagues in Rome studied the results of bombarding uranium with neutrons in 1934.[11] Fermi concluded that his experiments had created a new element with 94 protons, which he dubbed Hesperium. However, not all were convinced with Fermi's analysis of his results. The German chemist Ida Noddack notably suggested in 1934 that instead of creating a new, heavier element, that "it is conceivable that the nucleus breaks up into several large fragments."[12][13] However, Noddack's conclusion was not pursued.
 The experimental apparatus with which Otto Hahn and Fritz Strassmann discovered nuclear fission in 1938
The experimental apparatus with which Otto Hahn and Fritz Strassmann discovered nuclear fission in 1938
After the Fermi publication, Otto Hahn, Lise Meitner, and Fritz Strassmann began performing similar experiments in Berlin. Meitner, an Austrian Jew, lost her citizenship with the Anschluss in 1938. She fled and wound up in Sweden, but continued to collaborate by mail and through meetings with Hahn in Sweden. By coincidence her nephew Otto Robert Frisch, also a refugee, was also in Sweden when Meitner received a letter from Hahn describing his chemical proof that some of the product of the bombardment of uranium with neutrons was barium. Hahn was unsure of what the physical basis for the results were—barium had an atomic mass 40% less than uranium, and no previously known methods of radioactive decay could account for such a radical difference in the size of the nucleus. In Sweden, Frisch was skeptical, but Meitner trusted Hahn's ability as a chemist. Marie Curie had been separating barium from radium for many years, and the techniques were well-known. According to Frisch:
Was it a mistake? No, said Lise Meitner; Hahn was too good a chemist for that. But how could barium be formed from uranium? No larger fragments than protons or helium nuclei (alpha particles) had ever been chipped away from nuclei, and to chip off a large number not nearly enough energy was available. Nor was it possible that the uranium nucleus could have been cleaved right across. A nucleus was not like a brittle solid that can be cleaved or broken; George Gamow had suggested early on, and Bohr had given good arguments that a nucleus was much more like a liquid drop. Perhaps a drop could divide itself into two smaller drops in a more gradual manner, by first becoming elongated, then constricted, and finally being torn rather than broken in two? We knew that there were strong forces that would resist such a process, just as the surface tension of an ordinary liquid drop tends to resist its division into two smaller ones. But nuclei differed from ordinary drops in one important way: they were electrically charged, and that was known to counteract the surface tension.
The charge of a uranium nucleus, we found, was indeed large enough to overcome the effect of the surface tension almost completely; so the uranium nucleus might indeed resemble a very wobbly unstable drop, ready to divide itself at the slightest provocation, such as the impact of a single neutron. But there was another problem. After separation, the two drops would be driven apart by their mutual electric repulsion and would acquire high speed and hence a very large energy, about 200 MeV in all; where could that energy come from? ...Lise Meitner... worked out that the two nuclei formed by the division of a uranium nucleus together would be lighter than the original uranium nucleus by about one-fifth the mass of a proton. Now whenever mass disappears energy is created, according to Einstein's formula E=mc2, and one-fifth of a proton mass was just equivalent to 200MeV. So here was the source for that energy; it all fitted![14]
In short, Meitner had correctly interpreted Hahn's results to mean that the nucleus of uranium had split roughly in half. Frisch named the process "fission" as an analogy to binary fission in the biological sciences.
In December 1938, the German chemists Otto Hahn and Fritz Strassmann sent a manuscript to Naturwissenschaften reporting they had detected the element barium after bombarding uranium with neutrons;[15] simultaneously, they communicated these results to Lise Meitner. Meitner, and her nephew Otto Robert Frisch, correctly interpreted these results as being nuclear fission.[16] Frisch confirmed this experimentally on 13 January 1939.[17] In 1944, Hahn received the Nobel Prize for Chemistry for the discovery of nuclear fission. Some historians who have documented the history of the discovery of nuclear fission believe Meitner should have been awarded the Nobel Prize with Hahn.[18][19][20]
News spread quickly of the new discovery, which was correctly seen as an entirely novel physical effect with great scientific—and potentially practical—possibilities. Meitner’s and Frisch’s interpretation of the work of Hahn and Strassmann crossed the Atlantic Ocean with Niels Bohr, who was to lecture at Princeton University. I.I. Rabi and Willis Lamb, two Columbia University physicists working at Princeton, heard the news and carried it back to Columbia. Rabi said he told Enrico Fermi; Fermi gave credit to Lamb. Bohr soon thereafter went from Princeton to Columbia to see Fermi. Not finding Fermi in his office, Bohr went down to the cyclotron area and found Herbert L. Anderson. Bohr grabbed him by the shoulder and said: “Young man, let me explain to you about something new and exciting in physics.”[21] It was clear to a number of scientists at Columbia that they should try to detect the energy released in the nuclear fission of uranium from neutron bombardment. On 25 January 1939, a Columbia University team conducted the first nuclear fission experiment in the United States,[22] which was done in the basement of Pupin Hall; the members of the team were Herbert L. Anderson, Eugene T. Booth, John R. Dunning, Enrico Fermi, G. Norris Glasoe, and Francis G. Slack. The experiment involved placing uranium oxide inside of an ionization chamber and irradiating it with neutrons, and measuring the energy thus released. The results confirmed that fission was occurring and hinted strongly that it was the isotope uranium 235 in particular that was fissioning. The next day, the Fifth Washington Conference on Theoretical Physics began in Washington, D.C. under the joint auspices of the George Washington University and the Carnegie Institution of Washington. There, the news on nuclear fission was spread even further, which fostered many more experimental demonstrations.[23]
During this period, the Hungarian physicist Leó Szilárd who was residing at the United States, realized that the neutron-driven fission of heavy atoms could be used to create a nuclear chain reaction. Such a nuclear-reaction using neutrons was an idea he had first formulated in 1933, upon reading Rutherford's disparaging remarks about generating power from his team's 1932 experiment using protons to split lithium. However, Szilárd had not been able to achieve a neutron-driven chain reaction with neutron-rich light atoms. In such neutron-driven nuclear chain reactions, if the number of secondary neutrons produced by each reaction was greater than one, then each fission reaction could, in theory, trigger two more reactions. Such a system of exponential growth held out the possibility of using uranium fission as a means to generate large amounts of energy, either for civilian (i.e. electric) purposes, or even for military purposes—an atomic bomb.
Szilard now urged Fermi (in New York) and Frédéric Joliot-Curie (in Paris) to refrain from publishing on the possibility of a chain reaction, lest the Nazi government become aware of the possibilities on the eve of World War II. Fermi agreed to self-censor, with some hesitation. Joliot-Curie, however, did not, and in April 1939, his team in Paris (Joliot-Curie, Hans von Halban, and Lew Kowarski) reported in Nature that the number of neutrons emitted with nuclear fission of 235U was then reported at 3.5 per fission.[24] (They later corrected this to 2.6 per fission.) Simultaneous work by Szilard and Walter Zinn confirmed these results. This appeared to make the possibility of building nuclear reactors (first called "neutronic reactors" by Szilard and Fermi), and perhaps even nuclear bombs, in theory. There was still much unknown about fission and chain reacting systems, however.
The fission chain reaction
"Chain reactions" at that time were a known phenomenon in chemistry, but the analogous process in nuclear physics, using neutrons, had been foreseen as early as 1933 by Szilárd, although Szilárd at that time had no idea with what materials the process might be initiated. Szilárd considered that neutrons would be ideal for such a situation, since they lacked an electrostatic charge.
With the news of fission neutrons from uranium fission, Szilárd immediately understood the possibility of a nuclear chain reaction using uranium. In the summer, Fermi and Szilard proposed the idea of a nuclear reactor (pile) to mediate this process. The pile would use natural uranium as fuel. Fermi had shown much earlier that neutrons were far more effectively captured by atoms if they were of low energy (so-called "slow" or "thermal" neutrons), because for quantum reasons it made the atoms look like much larger targets to the neutrons. Thus to slow down the secondary neutrons released by the fissioning uranium nuclei, Fermi and Szilard proposed a graphite "moderator," against which the fast, high-energy secondary neutrons would collide, effectively slowing them down. With enough uranium, and with pure-enough graphite, their "pile" could theoretically sustain a slow-neutron chain reaction. This would result in the production of heat, as well as the creation of radioactive fission products.
In August 1939, Szilard and fellow Hungarian refugees physicists Teller and Wigner thought that the Germans might make use of the fission chain reaction and were spurred to attempt to attract the attention of the United States government to the issue. Towards this, they persuaded German-Jewish refugee Albert Einstein to lend his name to a letter directed to President Franklin Roosevelt. The Einstein–Szilárd letter suggested the possibility of a uranium bomb deliverable by ship, which would destroy "an entire harbor and much of the surrounding countryside." The President received the letter on 11 October 1939 — shortly after World War II began in Europe, but two years before U.S. entry into it. Roosevelt ordered that a scientific committee be authorized for overseeing uranium work and allocated a small sum of money for pile research.
In England, James Chadwick proposed an atomic bomb utilizing natural uranium, based on a paper by Rudolf Peierls with the mass needed for critical state being 30–40 tons. In America, J. Robert Oppenheimer thought that a cube of uranium deuteride 10 cm on a side (about 11 kg of uranium) might "blow itself to hell." In this design it was still thought that a moderator would need to be used for nuclear bomb fission (this turned out not to be the case if the fissile isotope was separated). In December, Heisenberg delivered a report to the German Ministry of War on the possibility of a uranium bomb. Most of these models were still under the assumption that the bombs would be powered by slow neutron reactions—and thus be similar to a reactor undergoing a meltdown.
In Birmingham, England, Frisch teamed up with Peierls, a fellow German-Jewish refugee. They had the idea of using a purified mass of the uranium isotope 235U, which had a cross section just determined, and which was much larger than that of 238U or natural uranium (which is 99.3% the latter isotope). Assuming that the cross section for fast-neutron fission of 235U was the same as for slow neutron fission, they determined that a pure 235U bomb could have a critical mass of only 6 kg instead of tons, and that the resulting explosion would be tremendous. (The amount actually turned out to be 15 kg, although several times this amount was used in the actual uranium (Little Boy) bomb). In February 1940 they delivered the Frisch–Peierls memorandum. Ironically, they were still officially considered "enemy aliens" at the time. Glenn Seaborg, Joseph W. Kennedy, Arthur Wahl and Italian-Jewish refugee Emilio Segrè shortly discovered 239Pu in the decay products of 239U produced by bombarding 238U with neutrons, and determined it to be a fissile material, like 235U.
The possibility of isolating uranium-235 was technically daunting, because uranium-235 and uranium-238 are chemically identical, and vary in their mass by only the weight of three neutrons. However, if a sufficient quantity of uranium-235 could be isolated, it would allow for a fast neutron fission chain reaction. This would be extremely explosive, a true "atomic bomb." The discovery that plutonium-239 could be produced in a nuclear reactor pointed towards another approach to a fast neutron fission bomb. Both approaches were extremely novel and not yet well understood, and there was considerable scientific skepticism at the idea that they could be developed in a short amount of time.
On June 28, 1941, the Office of Scientific Research and Development was formed in the U.S. to mobilize scientific resources and apply the results of research to national defense. In September, Fermi assembled his first nuclear "pile" or reactor, in an attempt to create a slow neutron-induced chain reaction in uranium, but the experiment failed to achieve criticality, due to lack of proper materials, or not enough of the proper materials which were available.
Producing a fission chain reaction in natural uranium fuel was found to be far from trivial. Early nuclear reactors did not use isotopically enriched uranium, and in consequence they were required to use large quantities of highly purified graphite as neutron moderation materials. Use of ordinary water (as opposed to heavy water) in nuclear reactors requires enriched fuel — the partial separation and relative enrichment of the rare 235U isotope from the far more common 238U isotope. Typically, reactors also require inclusion of extremely chemically pure neutron moderator materials such as deuterium (in heavy water), helium, beryllium, or carbon, the latter usually as graphite. (The high purity for carbon is required because many chemical impurities such as the boron-10 component of natural boron, are very strong neutron absorbers and thus poison the chain reaction and end it prematurely.)
Production of such materials at industrial scale had to be solved for nuclear power generation and weapons production to be accomplished. Up to 1940, the total amount of uranium metal produced in the USA was not more than a few grams, and even this was of doubtful purity; of metallic beryllium not more than a few kilograms; and concentrated deuterium oxide (heavy water) not more than a few kilograms. Finally, carbon had never been produced in quantity with anything like the purity required of a moderator.
The problem of producing large amounts of high purity uranium was solved by Frank Spedding using the thermite or "Ames" process. Ames Laboratory was established in 1942 to produce the large amounts of natural (unenriched) uranium metal that would be necessary for the research to come. The critical nuclear chain-reaction success of the Chicago Pile-1 (December 2, 1942) which used unenriched (natural) uranium, like all of the atomic "piles" which produced the plutonium for the atomic bomb, was also due specifically to Szilard's realization that very pure graphite could be used for the moderator of even natural uranium "piles". In wartime Germany, failure to appreciate the qualities of very pure graphite led to reactor designs dependent on heavy water, which in turn was denied the Germans by Allied attacks in Norway, where heavy water was produced. These difficulties—among many others— prevented the Nazis from building a nuclear reactor capable of criticality during the war, although they did never put as much effort as the United States into nuclear research, focussing on other technologies (see German nuclear energy project for more details).
Manhattan Project and beyond
In the United States, an all-out effort for making atomic weapons was begun in late 1942. This work was taken over by the U.S. Army Corps of Engineers in 1943, and known as the Manhattan Engineer District. The top-secret Manhattan Project, as it was colloquially known, was led by General Leslie R. Groves. Among the project's dozens of sites were: Hanford Site in Washington state, which had the first industrial-scale nuclear reactors; Oak Ridge, Tennessee, which was primarily concerned with uranium enrichment; and Los Alamos, in New Mexico, which was the scientific hub for research on bomb development and design. Other sites, notably the Berkeley Radiation Laboratory and the Metallurgical Laboratory at the University of Chicago, played important contributing roles. Overall scientific direction of the project was managed by the physicist J. Robert Oppenheimer.
In July 1945, the first atomic bomb, dubbed "Trinity", was detonated in the New Mexico desert. It was fueled by plutonium created at Hanford. In August 1945, two more atomic bombs—"Little Boy", a uranium-235 bomb, and "Fat Man", a plutonium bomb—were used against the Japanese cities of Hiroshima and Nagasaki.
In the years after World War II, many countries were involved in the further development of nuclear fission for the purposes of nuclear reactors and nuclear weapons.
Natural fission chain-reactors on Earth
Criticality in nature is uncommon. At three ore deposits at Oklo in Gabon, sixteen sites (the so-called Oklo Fossil Reactors) have been discovered at which self-sustaining nuclear fission took place approximately 2 billion years ago. Unknown until 1972 (but postulated by Paul Kuroda in 1956[25]), when French physicist Francis Perrin discovered the Oklo Fossil Reactors, it was realized that nature had beaten humans to the punch. Large-scale natural uranium fission chain reactions, moderated by normal water, had occurred far in the past and would not be possible now. This ancient process was able to use normal water as a moderator only because 2 billion years before the present, natural uranium was richer in the shorter-lived fissile isotope 235U (about 3%), than natural uranium available today (which is only 0.7%, and must be enriched to 3% to be usable in light-water reactors).
See also
- Photofission
- Nuclear Fusion
References
- ^ Arora, M. G.; Singh, M. (1994). Nuclear Chemistry. Anmol Publications. p. 202. ISBN 81-261-1763-X. http://books.google.com/books?id=G3JA5pYeQcgC&pg=PA202. Retrieved 2011-04-02.
- ^ Saha, Gopal (2010). Fundamentals of Nuclear Pharmacy (Sixth ed.). Springer Science+Business Media. p. 11. ISBN 1-4419-5859-2. http://books.google.com/books?id=bEXqI4ACk-AC&pg=PA11. Retrieved 2011-04-02.
- ^ [1] Comparative study of the ternary particle emission in 243-Cm (nth,f) and 244-Cm(SF). S. Vermote, et. al. in Dynamical aspects of nuclear fission: proceedings of the 6th International Conference. Ed. J. Kliman, M. G. Itkis, S. Gmuca. World Scientific Publishing Co. Pte. Ltd. Singapore. (2008)
- ^ Hans A. Bethe, "The Hydrogen Bomb", Bulletin of the Atomic Scientists, April 1950, page 99. Fetched from books.google.com on 18 April 2011.
- ^ Nuclear Fission and Fusion, and Nuclear Interactions. NLP National Physical Laboratory. 2008. Retrieved 2009-06-25.
- ^ L. Bonneau; P. Quentin. "Microscopic calculations of potential energy surfaces: fission and fusion properties". http://google.com/search?q=cache:U_nWMesl81IJ:t16web.lanl.gov/publications/bonneau2.pdf+fission+mass+ratios+most+probable&hl=en&gl=us&ct=clnk&cd=4ing. Retrieved 2008-07-28.
- ^ "Frequently Asked Questions #1". Radiation Effects Research Foundation. http://www.rerf.or.jp/general/qa_e/qa1.html. Retrieved Sept. 18, 2007.
- ^ E. Rutherford (1911). "The scattering of α and β particles by matter and the structure of the atom". Philosophical Magazine 21: 669–688. http://web.ihep.su/dbserv/compas/src/rutherford11/eng.pdf.
- ^ Cockcroft and Walton split lithium with high energy protons April 1932.
- ^ Chadwick announced his initial findings in: Chadwick, J. (1932). "Possible Existence of a Neutron". Nature 129 (3252): 312. Bibcode 1932Natur.129Q.312C. doi:10.1038/129312a0. http://web.mit.edu/22.54/resources/Chadwick.pdf. Subsequently he communicated his findings in more detail in: Chadwick, J. (1932). "The existence of a neutron". Proceedings of the Royal Society, Series A 136 (830): 692–708. Bibcode 1932RSPSA.136..692C. doi:10.1098/rspa.1932.0112. http://www.chemteam.info/Chem-History/Chadwick-1932/Chadwick-neutron.html.; and Chadwick, J. (1933). "The Bakerian Lecture: The neutron". Proceedings of the Royal Society, Series A 142 (846): 1–25. Bibcode 1933RSPSA.142....1C. doi:10.1098/rspa.1933.0152.
- ^ E. Fermi, E. Amaldi, O. D'Agostino, F. Rasetti, and E. Segrè (1934) "Radioattività provocata da bombardamento di neutroni III," La Ricerca Scientifica, vol. 5, no. 1, pages 452–453.
- ^ Ida Noddack (1934). "Über das Element 93". Zeitschrift für Angewandte Chemie 47 (37): 653. doi:10.1002/ange.19340473707. http://www.chemteam.info/Chem-History/Noddack-1934.html.
- ^ Tacke, Ida Eva. Astr.ua.edu. Retrieved on 2010-12-24.
- ^ Weintraub, Bob. Lise Meitner (1878–1968): Protactinium, Fission, and Meitnerium. Retrieved on June 8, 2009.
- ^ O. Hahn and F. Strassmann (1939). "Über den Nachweis und das Verhalten der bei der Bestrahlung des Urans mittels Neutronen entstehenden Erdalkalimetalle ("On the detection and characteristics of the alkaline earth metals formed by irradiation of uranium with neutrons")". Naturwissenschaften 27 (1): 11–15. Bibcode 1939NW.....27...11H. doi:10.1007/BF01488241.. The authors were identified as being at the Kaiser-Wilhelm-Institut für Chemie, Berlin-Dahlem. Received 22 December 1938.
- ^ Meitner, Lise; Frisch, O. R. (1939). "Disintegration of Uranium by Neutrons: a New Type of Nuclear Reaction". Nature 143 (3615): 239. Bibcode 1939Natur.143..239M. doi:10.1038/143239a0. http://www.nature.com/physics/looking-back/meitner/index.html.. The paper is dated 16 January 1939. Meitner is identified as being at the Physical Institute, Academy of Sciences, Stockholm. Frisch is identified as being at the Institute of Theoretical Physics, University of Copenhagen.
- ^ Frisch, O. R. (1939). "Physical Evidence for the Division of Heavy Nuclei under Neutron Bombardment". Nature 143 (3616): 276. Bibcode 1939Natur.143..276F. doi:10.1038/143276a0. http://dbhs.wvusd.k12.ca.us/webdocs/Chem-History/Frisch-Fission-1939.html.[dead link]. The paper is dated 17 January 1939. [The experiment for this letter to the editor was conducted on 13 January 1939; see Richard Rhodes The Making of the Atomic Bomb. 263 and 268 (Simon and Schuster, 1986).]
- ^ Ruth Lewin Sime. From Exceptional Prominence to Prominent Exception: Lise Meitner at the Kaiser Wilhelm Institute for Chemistry Ergebnisse 24 Forschungsprogramm Geschichte der Kaiser-Wilhelm-Gesellschaft im Nationalsozialismus (2005).
- ^ Ruth Lewin Sime. Lise Meitner: A Life in Physics (University of California, 1997).
- ^ Crawford, Elisabeth; Sime, Ruth Lewin; Walker, Mark (1997). "A Nobel Tale of Postwar Injustice". Physics Today 50 (9): 26. Bibcode 1997PhT....50i..26C. doi:10.1063/1.881933.
- ^ Richard Rhodes. The Making of the Atomic Bomb, 268 (Simon and Schuster, 1986) ISBN 0671441337.
- ^ Anderson, H.; Booth, E.; Dunning, J.; Fermi, E.; Glasoe, G.; Slack, F. (1939). "The Fission of Uranium". Physical Review 55 (5): 511. Bibcode 1939PhRv...55..511A. doi:10.1103/PhysRev.55.511.2.
- ^ Richard Rhodes. The Making of the Atomic Bomb, 267–270 (Simon and Schuster, 1986) ISBN 0671441337.
- ^ Von Halban, H.; Joliot, F.; Kowarski, L. (1939). "Number of Neutrons Liberated in the Nuclear Fission of Uranium". Nature 143 (3625): 680. Bibcode 1939Natur.143..680V. doi:10.1038/143680a0.
- ^ Kuroda, P. K. (1956). "On the Nuclear Physical Stability of the Uranium Minerals". The Journal of Chemical Physics 25 (4): 781. Bibcode 1956JChPh..25..781K. doi:10.1063/1.1743058. http://nuclearplanet.com/Kuroda%201956.pdf.
- DOE Fundamentals Handbook: Nuclear Physics and Reactor Theory Volume 1. U.S. Department of Energy. January 1993. http://www.hss.doe.gov/nuclearsafety/ns/techstds/standard/hdbk1019/h1019v1.pdf. Retrieved 2009-02-01.
- DOE Fundamentals Handbook: Nuclear Physics and Reactor Theory Volume 2. U.S. Department of Energy. January 1993. http://www.hss.doe.gov/nuclearsafety/ns/techstds/standard/hdbk1019/h1019v2.pdf. Retrieved 2009-02-01.
External links
- The Effects of Nuclear Weapons
- Annotated bibliography for nuclear fission from the Alsos Digital Library
- The Discovery of Nuclear Fission Historical account complete with audio and teacher's guides from the American Institute of Physics History Center
- atomicarchive.com Nuclear Fission Explained
- Nuclear Files.org What is Nuclear Fission?
- Nuclear Fission Animation
Nuclear technology Science Fuel Deuterium · Fertile material · Fissile · Isotope separation · Plutonium · Thorium · Tritium · Uranium (enriched • depleted)Neutron Activation · Capture · Cross-section · Fast · Fusion · Generator · Poison · Radiation · Reflector · Temp · ThermalReactors Boiling (BWR · ABWR) · Heavy (CANDU · PHWR · SGHWR) · Natural (NFR) · Pressurized (PWR · VVER · EPR) · Supercritical (SCWR)Advanced gas-cooled (AGR) · Magnox · Pebble bed (PBMR) · RBMK · UHTREX · Very high temperature (VHTR)FLiBeNone
(Fast)Breeder (FBR) · Integral (IFR) · Liquid-metal-cooled (LMFR) · SSTAR · Traveling Wave (TWR)
Generation IV by coolant: (Gas (GFR) · Lead (LFR) · Sodium (SFR))OtherPower Medicine TherapyWeapon TopicsListsWaste ProductsActinide: (Reprocessed uranium · Reactor-grade plutonium · Minor actinide) · Activation · Fission (LLFP)DisposalDebate Nuclear power debate · Nuclear weapons debate · Anti-nuclear movement · Uranium mining debate · Nuclear power phase-outRadiation (Physics & Health) Main articles Background radiation · Cosmic ray · Gamma ray · Nuclear fission · Nuclear fusion · Nuclear radiation (Nuclear reactors · Nuclear weapons) · Particle accelerators · Radioactive materials (Radioactive decay) · X-rayElectromagnetic radiation
and healthRadiation therapy · Radiation poisoning · Radioactivity in the life sciences · List of civilian radiation accidents
Health physics · Laser safety · Lasers and aviation safety · Mobile phone radiation and health · Wireless electronic devices and healthRelated articles Energy Fundamental concepts Primary energy sources Fossil fuel (Coal, Petroleum, Natural gas) · Mineral fuel (Natural uranium) · Solar · Wind · Bioenergy (Biomass) · Water (Hydroenergy, Marine energy) · GeothermalEnergy carriers Energy systems Oil refinery · Fossil fuel power station (Coal-fired power plant, IGCC power plant, CHP plant) · Nuclear power (Nuclear power plant) · Solar power (Photovoltaic power plant, CSP plant) · Solar thermal energy (Solar power tower, Solar furnace) · Wind power (Wind farm, Offshore wind farm, Small-scale wind turbine, HAWP plant) · Hydropower (Hydropower plant, Wave farm, Tidal power station) · Biomass-fueled power plant · Geothermal power plantCategories:- Nuclear physics
- Fundamental physics concepts
- Nuclear chemistry
- Radioactivity
Wikimedia Foundation. 2010.