Viscosity

For other uses, see Viscosity (disambiguation).

Viscosity
The substance above has lower viscosity than the substance below
SI symbol:	μ, η
SI unit:	Pa·s = kg/(s·m)
Derivations from other quantities:	μ = G·t

Continuum mechanics
Laws Conservation of mass Conservation of momentum Conservation of energy Entropy inequality
Solid mechanics Solids Stress · Deformation Compatibility Finite strain · Infinitesimal strain Elasticity (linear) · Plasticity Bending · Hooke's law Failure theory Fracture mechanics Frictionless/Frictional Contact mechanics
Fluid mechanics Fluids Fluid statics · Fluid dynamics Surface tension Navier–Stokes equations Viscosity: Newtonian, Non-Newtonian
Rheology Viscoelasticity Smart fluids: Magnetorheological Electrorheological Ferrofluids Rheometry · Rheometer
Scientists Bernoulli · Cauchy · Hooke Navier · Newton · Stokes · Jamal Nazrul Islam · Fazle Hussain
v · d · e

Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms (and for fluids only), viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity. Put simply, the less viscous the fluid is, the greater its ease of movement (fluidity).^[1]

Viscosity describes a fluid's internal resistance to flow and may be thought of as a measure of fluid friction. For example, high-viscosity felsic magma will create a tall, steep stratovolcano, because it cannot flow far before it cools, while low-viscosity mafic lava will create a wide, shallow-sloped shield volcano. All real fluids (except superfluids) have some resistance to stress and therefore are viscous, but a fluid which has no resistance to shear stress is known as an ideal fluid or inviscid fluid.

The study of flowing matter is known as rheology, which includes viscosity and related concepts.

Etymology

The word "viscosity" is derived from the Latin "viscum alba", meaning white mistletoe. A viscous glue called birdlime was made from mistletoe berries and was used for lime-twigs to catch birds.^[2]

Properties and behavior

Overview

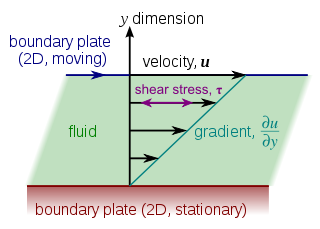Laminar shear of fluid between two plates. Friction between the fluid and the moving boundaries causes the fluid to shear. The force required for this action is a measure of the fluid's viscosity. This type of flow is known as a Couette flow.

Laminar shear, the non-constant gradient, is a result of the geometry the fluid is flowing through (e.g. a pipe).

In general, in any flow, layers move at different velocities and the fluid's viscosity arises from the shear stress between the layers that ultimately opposes any applied force. The relationship between the shear stress and the velocity gradient can be obtained by considering two plates closely spaced at a distance y, and separated by a homogeneous substance. Assuming that the plates are very large, with a large area A, such that edge effects may be ignored, and that the lower plate is fixed, let a force F be applied to the upper plate. If this force causes the substance between the plates to undergo shear flow with a velocity gradient u/y (as opposed to just shearing elastically until the shear stress in the substance balances the applied force), the substance is called a fluid.

The applied force is proportional to the area and velocity gradient in the fluid:

$F=\mu A \frac{u}{y}$,

where μ is the proportionality factor called dynamic viscosity.

This equation can be expressed in terms of shear stress $\tau=\frac{F}{A}$. Thus as expressed in differential form by Isaac Newton for straight, parallel and uniform flow, the shear stress between layers is proportional to the velocity gradient in the direction perpendicular to the layers:

$\tau=\mu \frac{\partial u}{\partial y}$

Hence, through this method, the relation between the shear stress and the velocity gradient can be obtained.

Note that the rate of shear deformation is $\frac{u} {y}$ which can be also written as a shear velocity, $\frac{du} {dy}$.

James Clerk Maxwell called viscosity fugitive elasticity because of the analogy that elastic deformation opposes shear stress in solids, while in viscous fluids, shear stress is opposed by rate of deformation.

Types of viscosity

Viscosity, the slope of each line, varies among materials

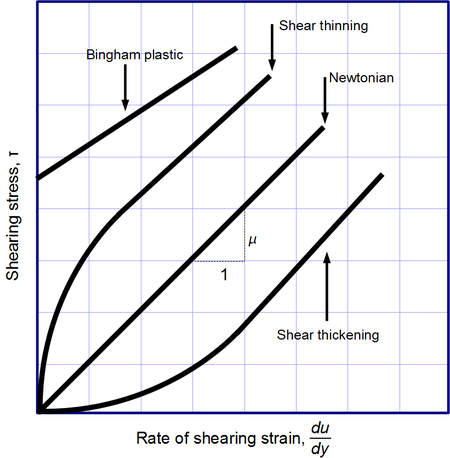
Newton's law of viscosity, given above, is a constitutive equation (like Hooke's law, Fick's law, Ohm's law). It is not a fundamental law of nature but an approximation that holds in some materials and fails in others. Non-Newtonian fluids exhibit a more complicated relationship between shear stress and velocity gradient than simple linearity. Thus there exist a number of forms of viscosity:

• Newtonian: fluids, such as water and most gases which have a constant viscosity.
• Shear thickening: viscosity increases with the rate of shear.
• Shear thinning: viscosity decreases with the rate of shear. Shear thinning liquids are very commonly, but misleadingly, described as thixotropic.
• Thixotropic: materials which become less viscous over time when shaken, agitated, or otherwise stressed.
• Rheopectic: materials which become more viscous over time when shaken, agitated, or otherwise stressed.
• A Bingham plastic is a material that behaves as a solid at low stresses but flows as a viscous fluid at high stresses.
• A magnetorheological fluid is a type of "smart fluid" which, when subjected to a magnetic field, greatly increases its apparent viscosity, to the point of becoming a viscoelastic solid.

Viscosity coefficients

Viscosity coefficients can be defined in two ways:

• Dynamic viscosity, also absolute viscosity, the more usual one (typical units Pa·s, Poise, P);
• Kinematic viscosity is the dynamic viscosity divided by the density (typical units cm²/s, Stokes, St).

Viscosity is a tensorial quantity that can be decomposed in different ways into two independent components. The most usual decomposition yields the following viscosity coefficients:

• Shear viscosity, the most important one, often referred to as simply viscosity, describing the reaction to applied shear stress; simply put, it is the ratio between the pressure exerted on the surface of a fluid, in the lateral or horizontal direction, to the change in velocity of the fluid as you move down in the fluid (this is what is referred to as a velocity gradient).
• Volume viscosity (also called bulk viscosity or second viscosity) becomes important only for such effects where fluid compressibility is essential. Examples would include shock waves and sound propagation. It appears in the Stokes' law (sound attenuation) that describes propagation of sound in Newtonian liquid.

Alternatively,

• Extensional viscosity, a linear combination of shear and bulk viscosity, describes the reaction to elongation, widely used for characterizing polymers. For example, at room temperature, water has a dynamic shear viscosity of about 1.0×10⁻³ Pa·s and motor oil of about 250×10⁻³ Pa·s.^[3]

Viscosity measurement

Main article: Viscometer

Viscosity is measured with various types of viscometers and rheometers. A rheometer is used for those fluids which cannot be defined by a single value of viscosity and therefore require more parameters to be set and measured than is the case for a viscometer. Close temperature control of the fluid is essential to accurate measurements, particularly in materials like lubricants, whose viscosity can double with a change of only 5 °C.

For some fluids, viscosity is a constant over a wide range of shear rates (Newtonian fluids). The fluids without a constant viscosity (non-Newtonian fluids) cannot be described by a single number. Non-Newtonian fluids exhibit a variety of different correlations between shear stress and shear rate.

One of the most common instruments for measuring kinematic viscosity is the glass capillary viscometer.

In paint industries, viscosity is commonly measured with a Zahn cup, in which the efflux time is determined and given to customers. The efflux time can also be converted to kinematic viscosities (centistokes, cSt) through the conversion equations.

Also used in paint, a Stormer viscometer uses load-based rotation in order to determine viscosity. The viscosity is reported in Krebs units (KU), which are unique to Stormer viscometers.

A Ford viscosity cup measures the rate of flow of a liquid. This, under ideal conditions, is proportional to the kinematic viscosity.

Vibrating viscometers can also be used to measure viscosity. These models such as the Dynatrol use vibration rather than rotation to measure viscosity.

Extensional viscosity can be measured with various rheometers that apply extensional stress.

Volume viscosity can be measured with an acoustic rheometer.

Apparent viscosity is a calculation derived from tests performed on drilling fluid used in oil or gas well development. These calculations and tests help engineers develop and maintain the properties of the drilling fluid to the specifications required.

Units

Dynamic viscosity

The usual symbol for dynamic viscosity used by mechanical and chemical engineers — as well as fluid dynamicists — is the Greek letter mu (μ).^[4][5][6] The symbol η is also used by chemists, physicists, and the IUPAC.^[7]

The SI physical unit of dynamic viscosity is the pascal-second (Pa·s), (equivalent to N·s/m², or kg/(m·s)). If a fluid with a viscosity of one Pa·s is placed between two plates, and one plate is pushed sideways with a shear stress of one pascal, it moves a distance equal to the thickness of the layer between the plates in one second. Water at 20 °C has a viscosity of 0.001002 Pa·s.

The cgs physical unit for dynamic viscosity is the poise^[8] (P), named after Jean Louis Marie Poiseuille. It is more commonly expressed, particularly in ASTM standards, as centipoise (cP). Water at 20 °C has a viscosity of 1.0020 cP.

1 P = 0.1 Pa·s,

1 cP = 1 mPa·s = 0.001 Pa·s.

Kinematic viscosity

In many situations, we are concerned with the ratio of the inertial force to the viscous force (i.e. the Reynolds number, Re = VD / ν), the former characterized by the fluid density ρ. This ratio is characterized by the kinematic viscosity (Greek letter nu, ν), defined as follows:

$\nu = \frac {\mu} {\rho}$

The SI unit of ν is m²/s. The SI unit of ρ is kg/m³.

The cgs physical unit for kinematic viscosity is the stokes (St), named after George Gabriel Stokes. It is sometimes expressed in terms of centiStokes (cSt). In U.S. usage, stoke is sometimes used as the singular form.

1 St = 1 cm²·s⁻¹ = 10⁻⁴ m²·s⁻¹.

1 cSt = 1 mm²·s⁻¹ = 10⁻⁶m²·s⁻¹.

Water at 20 °C has a kinematic viscosity of about 1 cSt.

The kinematic viscosity is sometimes referred to as diffusivity of momentum, because it is analogous to diffusivity of heat and diffusivity of mass. It is therefore used in dimensionless numbers which compare the ratio of the diffusivities.

Fluidity

The reciprocal of viscosity is fluidity, usually symbolized by φ = 1 / μ or F = 1 / μ, depending on the convention used, measured in reciprocal poise (cm·s·g⁻¹), sometimes called the rhe. Fluidity is seldom used in engineering practice.

The concept of fluidity can be used to determine the viscosity of an ideal solution. For two components a and b, the fluidity when a and b are mixed is

$F \approx \chi_a F_a + \chi_b F_b,$

which is only slightly simpler than the equivalent equation in terms of viscosity:

$\mu \approx \frac{1}{\chi_a /\mu_a + \chi_b/\mu_b},$

where χ_a and χ_b is the mole fraction of component a and b respectively, and μ_a and μ_b are the components pure viscosities.

Non-standard units

The Reyn is a British unit of dynamic viscosity.

Viscosity index is a measure for the change of kinematic viscosity with temperature. It is used to characterise lubricating oil in the automotive industry.

At one time the petroleum industry relied on measuring kinematic viscosity by means of the Saybolt viscometer, and expressing kinematic viscosity in units of Saybolt Universal Seconds (SUS).^[9] Other abbreviations such as SSU (Saybolt Seconds Universal) or SUV (Saybolt Universal Viscosity) are sometimes used. Kinematic viscosity in centistoke can be converted from SUS according to the arithmetic and the reference table provided in ASTM D 2161.^[10]

Molecular origins

Pitch has a viscosity approximately 230 billion (2.3×10¹¹) times that of water.^[11]

The viscosity of a system is determined by how molecules constituting the system interact. There are no simple but correct expressions for the viscosity of a fluid. The simplest exact expressions are the Green–Kubo relations for the linear shear viscosity or the Transient Time Correlation Function expressions derived by Evans and Morriss in 1985. Although these expressions are each exact in order to calculate the viscosity of a dense fluid, using these relations requires the use of molecular dynamics computer simulations.

Gases

Viscosity in gases arises principally from the molecular diffusion that transports momentum between layers of flow. The kinetic theory of gases allows accurate prediction of the behavior of gaseous viscosity.

Within the regime where the theory is applicable:

• Viscosity is independent of pressure and
• Viscosity increases as temperature increases.^[12]

James Clerk Maxwell published a famous paper in 1866 using the kinetic theory of gases to study gaseous viscosity.^[13] To understand why the viscosity is independent of pressure, consider two adjacent boundary layers (A and B) moving with respect to each other. The internal friction (the viscosity) of the gas is determined by the probability a particle of layer A enters layer B with a corresponding transfer of momentum. Maxwell's calculations showed him that the viscosity coefficient is proportional to both the density, the mean free path and the mean velocity of the atoms. On the other hand, the mean free path is inversely proportional to the density. So an increase of pressure doesn't result in any change of the viscosity.

Relation to mean free path of diffusing particles

In relation to diffusion, the kinematic viscosity provides a better understanding of the behavior of mass transport of a dilute species. Viscosity is related to shear stress and the rate of shear in a fluid, which illustrates its dependence on the mean free path, λ, of the diffusing particles.

From fluid mechanics, for a Newtonian fluid, the shear stress, τ, on a unit area moving parallel to itself, is found to be proportional to the rate of change of velocity with distance perpendicular to the unit area:

$\tau = \mu \frac{du_x}{dy}$

for a unit area parallel to the x-z plane, moving along the x axis. We will derive this formula and show how μ is related to λ.

Interpreting shear stress as the time rate of change of momentum, p, per unit area A (rate of momentum flux) of an arbitrary control surface gives

$\tau = \frac{\dot{p}}{A} = \frac{\dot{m} \langle u_x \rangle}{A}.$

where $\langle u_x \rangle$ is the average velocity along x of fluid molecules hitting the unit area, with respect to the unit area.

Further manipulation will show^[14]

$\dot{m} = \rho \bar{u} A$

$\langle u_x \rangle = \frac12\, \lambda\frac{du_x}{dy}$, assuming that molecules hitting the unit area come from all distances between 0 and λ (equally distributed), and that their average velocities change linearly with distance (always true for small enough λ). From this follows:

$\tau = \underbrace{\frac12\, \rho \bar{u} \lambda}_{\mu} \cdot \frac{du_x}{dy} \; \; \Rightarrow \; \; \nu = \frac{\mu}{\rho} = \tfrac12\, \bar{u} \lambda,$

where

$\dot{m}$ is the rate of fluid mass hitting the surface,

ρ is the density of the fluid,

ū is the average molecular speed ($\bar{u} = \sqrt{\langle u^2 \rangle}$),

μ is the dynamic viscosity.

Effect of temperature on the viscosity of a gas

Sutherland's formula can be used to derive the dynamic viscosity of an ideal gas as a function of the temperature:^[15]

${\mu} = {\mu}_0 \frac {T_0+C} {T + C} \left (\frac {T} {T_0} \right )^{3/2}.$

This in turn is equal to

$\lambda\,\frac{T^{3/2}}{T+C}\,,$  where  $\lambda = \frac{\mu_0(T_0+C)}{T_0^{3/2}}\,$  is a constant.

in Sutherland's formula:

• μ = dynamic viscosity in (Pa·s) at input temperature T,
• μ₀ = reference viscosity in (Pa·s) at reference temperature T₀,
• T = input temperature in kelvins,
• T₀ = reference temperature in kelvins,
• C = Sutherland's constant for the gaseous material in question.

Valid for temperatures between 0 < T < 555 K with an error due to pressure less than 10% below 3.45 MPa.

Sutherland's constant and reference temperature for some gases

Gas	C [K]	T0 [K]	μ0 [μPa s]
air	120	291.15	18.27
nitrogen	111	300.55	17.81
oxygen	127	292.25	20.18
carbon dioxide	240	293.15	14.8
carbon monoxide	118	288.15	17.2
hydrogen	72	293.85	8.76
ammonia	370	293.15	9.82
sulfur dioxide	416	293.65	12.54
helium	79.4 [16]	273	19 [17]

See also [1].

Viscosity of a dilute gas

The Chapman-Enskog equation^[18] may be used to estimate viscosity for a dilute gas. This equation is based on a semi-theoretical assumption by Chapman and Enskog. The equation requires three empirically determined parameters: the collision diameter (σ), the maximum energy of attraction divided by the Boltzmann constant (є/к) and the collision integral (ω(T^*)).

${\mu}_0 \times 10^6 = {2.6693}\frac {(MT)^{1/2}} {\sigma^{2}\omega(T^*)},$

with

• T^* = κT/ε — reduced temperature (dimensionless),
• μ₀ = viscosity for dilute gas (μPa.s),
• M = molecular mass (g/mol),
• T = temperature (K),
• σ = the collision diameter (Å),
• ε / κ = the maximum energy of attraction divided by the Boltzmann constant (K),
• ω_μ = the collision integral.

Liquids

Video showing three liquids with different Viscosities

In liquids, the additional forces between molecules become important. This leads to an additional contribution to the shear stress though the exact mechanics of this are still controversial.^{[citation needed]} Thus, in liquids:

• Viscosity is independent of pressure (except at very high pressure); and
• Viscosity tends to fall as temperature increases (for example, water viscosity goes from 1.79 cP to 0.28 cP in the temperature range from 0 °C to 100 °C); see temperature dependence of liquid viscosity for more details.

The dynamic viscosities of liquids are typically several orders of magnitude higher than dynamic viscosities of gases.

Viscosity of blends of liquids

The viscosity of the blend of two or more liquids can be estimated using the Refutas equation^[19]. The calculation is carried out in three steps.

The first step is to calculate the Viscosity Blending Number (VBN) (also called the Viscosity Blending Index) of each component of the blend:

(1)   $\mbox{VBN} = 14.534 \times \ln\left[ \ln(v + 0.8) \right] + 10.975\,$

where v is the kinematic viscosity in centistokes (cSt). It is important that the kinematic viscosity of each component of the blend be obtained at the same temperature.

The next step is to calculate the VBN of the blend, using this equation:

(2)   $\mbox{VBN}_\text{Blend} = \left[ x_A \times \mbox{VBN}_A \right] + \left[x_B \times \mbox{VBN}_B\right] + \cdots + \left[x_N \times \mbox{VBN}_N\right]\,$

where x_X is the mass fraction of each component of the blend.

Once the viscosity blending number of a blend has been calculated using equation (2), the final step is to determine the kinematic viscosity of the blend by solving equation (1) for v:

(3)   $v = \exp\left( \exp\left( \frac{\text{VBN}_\text{Blend} - 10.975}{14.534} \right) \right) - 0.8,$

where VBN_Blend is the viscosity blending number of the blend.

Viscosity of selected substances

The viscosity of air and water are by far the two most important materials for aviation aerodynamics and shipping fluid dynamics. Temperature plays the main role in determining viscosity.

Viscosity of air

Pressure dependence of the dynamic viscosity of dry air at the temperatures of 300, 400 and 500 K

The viscosity of air depends mostly on the temperature. At 15.0 °C, the viscosity of air is 1.78×10⁻⁵ kg/(m·s), 17.8 μPa.s or 1.78×10⁻⁵ Pa.s.. One can get the viscosity of air as a function of temperature from the Gas Viscosity Calculator

Viscosity of water

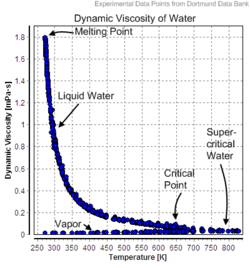
Dynamic Viscosity of Water

The dynamic viscosity of water is 8.90 × 10⁻⁴ Pa·s or 8.90 × 10⁻³ dyn·s/cm² or 0.890 cP at about 25 °C.
Water has a viscosity of 0.0091 poise at 25 °C, or 1 centipoise at 20 °C.
As a function of temperature T (K): (Pa·s) = A × 10^B/(T−C)
where A=2.414 × 10⁻⁵ Pa·s ; B = 247.8 K ; and C = 140 K.^[20]

Viscosity of liquid water at different temperatures up to the normal boiling point is listed below.

Temperature [°C]	Viscosity [mPa·s]
10	1.308
20	1.002
30	0.7978
40	0.6531
50	0.5471
60	0.4668
70	0.4044
80	0.3550
90	0.3150
100	0.2822

Viscosity of various materials

Example of the viscosity of milk and water. Liquids with higher viscosities will not make such a splash when poured at the same velocity.

Honey being drizzled.

Peanut butter is a semi-solid and can therefore hold peaks.

Some dynamic viscosities of Newtonian fluids are listed below:

Viscosity of selected gases at 100 kPa, [μPa·s] Gas at 0 °C (273 K) at 27 °C (300 K)[21] air 17.4 18.6 hydrogen 8.4 9.0 helium 20.0 argon 22.9 xenon 21.2 23.2 carbon dioxide 15.0 methane 11.2 ethane 9.5 Viscosity of fluids with variable compositions Fluid Viscosity [Pa·s] Viscosity [cP] honey 2–10 2,000–10,000 molasses 5–10 5,000–10,000 molten glass 10–1,000 10,000–1,000,000 chocolate syrup 10–25 10,000–25,000 molten chocolate* 45–130 [22] 45,000–130,000 ketchup* 50–100 50,000–100,000 lard ≈ 100 ≈ 100,000 peanut butter* ≈ 250 ≈ 250,000 shortening* ≈ 250 ≈ 250,000

Viscosity of liquids at 25 °C Liquid (): Viscosity [Pa·s] Viscosity [cP=mPa·s] acetone[23] 3.06×10−4 0.306 benzene[23] 6.04×10−4 0.604 blood (37 °C)[24] (3–4)×10−3 3–4 castor oil[23] 0.985 985 corn syrup[23] 1.3806 1380.6 ethanol[23] 1.074×10−3 1.074 ethylene glycol 1.61×10−2 16.1 glycerol[25] 1.2 (at 20 °C) 1200 HFO-380 2.022 2022 mercury[23] 1.526×10−3 1.526 methanol[23] 5.44×10−4 0.544 motor oil SAE 10 (20 °C)[12] 0.065 65 motor oil SAE 40 (20 °C)[12] 0.319 319 nitrobenzene[23] 1.863×10−3 1.863 liquid nitrogen @ 77K 1.58×10−4 0.158 propanol[23] 1.945×10−3 1.945 olive oil .081 81 pitch 2.3e8 2.3e11 quark–gluon plasma[26] 0 0 sulfuric acid[23] 2.42×10−2 24.2 water 8.94×10−4 0.894

* These materials are highly non-Newtonian.

Viscosity of slurry

The term slurry designs mixtures of a liquid and solid particles that retain some fluidity. The viscosity of slurry can be described as relative to the viscosity of the liquid phase:

$\mu_s = \mu_r \cdot \mu_l,$

where μ_s and μ_l are respectively the dynamic viscosity of the slurry and liquid (Pa·s), and μ_r is the relative viscosity (dimensionless).

Depending on the size and concentration of the solid particles, several models exist that describe the relative viscosity as a function of volume fraction ɸ of solid particles.

In the case of extremely low concentrations of fine particles, Einstein's equation^[27] may be used:

$\mu_r = 1 + 2.5 \cdot \phi$

In the case of higher concentrations, a modified equation was proposed by Guth and Simha^[28] which takes into account interaction between the solid particles:

$\mu_r = 1 + 2.5 \cdot \phi + 14.1 \cdot \phi^2$

Further modification of this equation was proposed by Thomas^[29] from the fitting of empirical data:

$\mu_r = 1 + 2.5 \cdot \phi + 10.05 \cdot \phi^2 + A \cdot e^{B \cdot \phi},$

where A = 0.00273 and B = 16.6.

In the case of very high concentrations, another empirical equation was proposed by Kitano et al.^[30]:

$\mu_r = (1 - \frac{\phi}{A})^{-2},$

where A = 0.68 for smooth spherical particles.

Viscosity of solids

On the basis that all solids such as granite^[31] flow in response to small shear stress, some researchers^[32] have contended that substances known as amorphous solids, such as glass and many polymers, may be considered to have viscosity. This has led some to the view that solids are simply "liquids" with a very high viscosity, typically greater than 10¹² Pa·s. This position is often adopted by supporters of the widely held misconception that glass flow can be observed in old buildings. This distortion is the result of the undeveloped glass making process of earlier eras, and not due to the viscosity of glass.^[33]

However, others argue that solids are, in general, elastic for small stresses while fluids are not.^[34] Even if solids flow at higher stresses, they are characterized by their low-stress behavior. This distinction is muddled if measurements are continued over long time periods, such as the Pitch drop experiment. Viscosity may be an appropriate characteristic for solids in a plastic regime. The situation becomes somewhat confused as the term viscosity is sometimes used for solid materials, for example Maxwell materials, to describe the relationship between stress and the rate of change of strain, rather than rate of shear.

These distinctions may be largely resolved by considering the constitutive equations of the material in question, which take into account both its viscous and elastic behaviors. Materials for which both their viscosity and their elasticity are important in a particular range of deformation and deformation rate are called viscoelastic. In geology, earth materials that exhibit viscous deformation at least three times greater than their elastic deformation are sometimes called rheids.

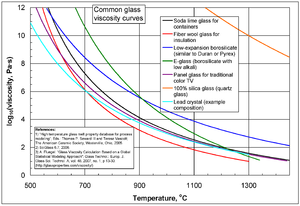
Viscosity of amorphous materials

Common glass viscosity curves.^[35]

Viscous flow in amorphous materials (e.g. in glasses and melts)^[36][37][38] is a thermally activated process:

$\mu = A \cdot e^{Q/RT},$

where Q is activation energy, T is temperature, R is the molar gas constant and A is approximately a constant.

The viscous flow in amorphous materials is characterized by a deviation from the Arrhenius-type behavior: Q changes from a high value Q_H at low temperatures (in the glassy state) to a low value Q_L at high temperatures (in the liquid state). Depending on this change, amorphous materials are classified as either

• strong when: Q_H − Q_L < Q_L or
• fragile when: Q_H − Q_L ≥ Q_L.

The fragility of amorphous materials is numerically characterized by the Doremus’ fragility ratio:

$R_D = \frac{Q_H}{Q_L}$

and strong material have R_D < 2 whereas fragile materials have R_D ≥ 2.

The viscosity of amorphous materials is quite exactly described by a two-exponential equation:

$\mu = A_1 \cdot T \cdot \left[1 + A_2 \cdot e^{B/RT}] \cdot [1 + C \cdot e^{D/RT} \right],$

with constants A₁, A₂, B, C and D related to thermodynamic parameters of joining bonds of an amorphous material.

Not very far from the glass transition temperature, T_g, this equation can be approximated by a Vogel-Fulcher-Tammann (VFT) equation.

If the temperature is significantly lower than the glass transition temperature, T < T_g, then the two-exponential equation simplifies to an Arrhenius type equation:

$\mu = A_LT \cdot e^{Q_H/RT}$

with:

$Q_H = H_d + H_m,\,$

where H_d is the enthalpy of formation of broken bonds (termed configuron s) and H_m is the enthalpy of their motion. When the temperature is less than the glass transition temperature, T < T_g, the activation energy of viscosity is high because the amorphous materials are in the glassy state and most of their joining bonds are intact.

If the temperature is highly above the glass transition temperature, T > T_g, the two-exponential equation also simplifies to an Arrhenius type equation:

$\mu = A_HT\cdot e^{Q_L/RT},$

with:

$Q_L = H_m.\,$

When the temperature is higher than the glass transition temperature, T > T_g, the activation energy of viscosity is low because amorphous materials are melt and have most of their joining bonds broken which facilitates flow.

Eddy viscosity

In the study of turbulence in fluids, a common practical strategy for calculation is to ignore the small-scale vortices (or eddies) in the motion and to calculate a large-scale motion with an eddy viscosity that characterizes the transport and dissipation of energy in the smaller-scale flow (see large eddy simulation). Values of eddy viscosity used in modeling ocean circulation may be from 5x10⁴ to 10⁶ Pa·s depending upon the resolution of the numerical grid.

The linear viscous stress tensor

For more details on an analogous development for linearly elastic materials, see Hooke's law and strain tensor.

Viscous forces in a fluid are a function of the rate at which the fluid velocity is changing over distance. The velocity at any point r is specified by the velocity field v(r). The velocity at a small distance dr from point r may be written as a Taylor series:

$\mathbf{v}(\mathbf{r}+d\mathbf{r}) = \mathbf{v}(\mathbf{r})+\frac{d\mathbf{v}}{d\mathbf{r}}d\mathbf{r}+\ldots,$

where dv / dr is shorthand for the dyadic product of the del operator and the velocity:

$\frac{d\mathbf{v}}{d\mathbf{r}} = \begin{bmatrix} \displaystyle{\frac{\partial v_x}{\partial x}} & \displaystyle{\frac{\partial v_x}{\partial y}} & \displaystyle{\frac{\partial v_x}{\partial z}}\\ \displaystyle{\frac{\partial v_y}{\partial x}} & \displaystyle{\frac{\partial v_y}{\partial y}} & \displaystyle{\frac{\partial v_y}{\partial z}}\\ \displaystyle{\frac{\partial v_z}{\partial x}} & \displaystyle{\frac{\partial v_z}{\partial y}} & \displaystyle{\frac{\partial v_z}{\partial z}} \end{bmatrix}.$

This is just the Jacobian of the velocity field.

Viscous forces are the result of relative motion between elements of the fluid, and so are expressible as a function of the velocity field. In other words, the forces at r are a function of v(r) and all derivatives of v(r) at that point. In the case of linear viscosity, the viscous force will be a function of the Jacobian tensor alone. For almost all practical situations, the linear approximation is sufficient.

If we represent x, y, and z by indices 1, 2, and 3 respectively, the i,j component of the Jacobian may be written as ∂_i v_j where ∂_i is shorthand for ∂/∂x_i. Note that when the first and higher derivative terms are zero, the velocity of all fluid elements is parallel, and there are no viscous forces.

Any matrix may be written as the sum of an antisymmetric matrix and a symmetric matrix, and this decomposition is independent of coordinate system, and so has physical significance. The velocity field may be approximated as:

$v_j(\mathbf{r}+d\mathbf{r}) = v_j(\mathbf{r})+\frac{1}{2}\left(\partial_i v_j-\partial_j v_i\right)dr_i + \frac{1}{2}\left(\partial_i v_j+\partial_j v_i\right)dr_i,$

where Einstein notation is now being used in which repeated indices in a product are implicitly summed. The second term from the right is the asymmetric part of the first derivative term, and it represents a rigid rotation of the fluid about r with angular velocity ω where:

$\omega=\frac12 \mathbf{\nabla}\times \mathbf{v}=\frac{1}{2}\begin{bmatrix} \partial_2 v_3-\partial_3 v_2\\ \partial_3 v_1-\partial_1 v_3\\ \partial_1 v_2-\partial_2 v_1 \end{bmatrix}.$

For such a rigid rotation, there is no change in the relative positions of the fluid elements, and so there is no viscous force associated with this term. The remaining symmetric term is responsible for the viscous forces in the fluid. Assuming the fluid is isotropic (i.e. its properties are the same in all directions), then the most general way that the symmetric term (the rate-of-strain tensor) can be broken down in a coordinate-independent (and therefore physically real) way is as the sum of a constant tensor (the rate-of-expansion tensor) and a traceless symmetric tensor (the rate-of-shear tensor):

$\frac{1}{2}\left(\partial_i v_j+\partial_j v_i\right) = \underbrace{\frac{1}{3}\partial_k v_k \delta_{ij}}_{\text{rate-of-expansion tensor}} + \underbrace{\left(\frac{1}{2}\left(\partial_i v_j+\partial_j v_i\right)-\frac{1}{3}\partial_k v_k \delta_{ij}\right)}_{\text{rate-of-shear tensor}},$

where δ_ij is the unit tensor. The most general linear relationship between the stress tensor σ and the rate-of-strain tensor is then a linear combination of these two tensors:^[39]

$\sigma_{\text{visc};ij} = \zeta\partial_k v_k \delta_{ij}+ \mu\left(\partial_i v_j+\partial_j v_i-\frac{2}{3}\partial_k v_k \delta_{ij}\right),$

where ς is the coefficient of bulk viscosity (or "second viscosity") and μ is the coefficient of (shear) viscosity.

The forces in the fluid are due to the velocities of the individual molecules. The velocity of a molecule may be thought of as the sum of the fluid velocity and the thermal velocity. The viscous stress tensor described above gives the force due to the fluid velocity only. The force on an area element in the fluid due to the thermal velocities of the molecules is just the hydrostatic pressure. This pressure term (−p δ_ij) must be added to the viscous stress tensor to obtain the total stress tensor for the fluid.

$\sigma_{ij} = -p\delta_{ij}+\sigma_{\text{visc};ij}.\,$

The infinitesimal force dF_i on an infinitesimal area dA_i is then given by the usual relationship:

$dF_i=\sigma_{ij}\, dA_j.\,$

See also

• Deborah number
• Dilatant
• Hyperviscosity syndrome
• Inviscid flow
• Reyn
• Reynolds number
• Trouton's ratio
• Viscoelasticity
• Viscosity index
• Joback method (estimation of the liquid viscosity from molecular structure)
• Microviscosity

References

1. ^ Symon, Keith (1971). Mechanics (Third ed.). Addison-Wesley. ISBN 0-201-07392-7. 
2. ^ "The Online Etymology Dictionary". Etymonline.com. http://www.etymonline.com/index.php?term=viscous. Retrieved 2010-09-14. 
3. ^ Raymond A. Serway (1996). Physics for Scientists & Engineers (4th ed.). Saunders College Publishing. ISBN 0-03-005932-1. 
4. ^ Victor Lyle Streeter, E. Benjamin Wylie, Keith W. Bedford Fluid Mechanics, McGraw-Hill, 1998 ISBN 0070625379
5. ^ J. P. Holman Heat Transfer, McGraw-Hill, 2002 ISBN 0071226214
6. ^ Frank P. Incropera, David P. DeWitt, Fundamentals of Heat and Mass Transfer, Wiley, 2007 ISBN 0471457280
7. ^ IUPAC Gold Book, Definition of (dynamic) viscosity
8. ^ "IUPAC definition of the Poise". http://www.iupac.org/goldbook/P04705.pdf#search=%22poise%20iupac%22. Retrieved 2010-09-14. 
9. ^ ASTM D 2161, Page one,(2005)
10. ^ "Quantities and Units of Viscosity". Uniteasy.com. http://www.uniteasy.com/en/unitguide/Viscosity.htm. Retrieved 2010-09-14. 
11. ^ Edgeworth,, R.; Dalton, B.J.; Parnell, T.. "The pitch drop experiment". University of Queensland. http://www.physics.uq.edu.au/physics_museum/pitchdrop.shtml. Retrieved 2009-03-31. . A copy of: European Journal of Physics (1984) pp. 198–200.
12. ^ ^{a b c} Glenn Elert. "The Physics Hypertextbook-Viscosity". Physics.info. http://physics.info/viscosity/. Retrieved 2010-09-14. 
13. ^ Maxwell, J. C. (1866). "On the viscosity or internal friction of air and other gases". Philosophical Transactions of the Royal Society of London 156: 249–268. doi:10.1098/rstl.1866.0013. 
14. ^ Salmon, R.L. (1998). Lectures on geophysical fluid dynamics. Oxford University Press. ISBN 0195108086. , pp. 23–26.
15. ^ Alexander J. Smits, Jean-Paul Dussauge Turbulent shear layers in supersonic flow, Birkhäuser, 2006, ISBN 0387261400 p. 46
16. ^ data constants for sutherland's formula
17. ^ Viscosity of liquids and gases
18. ^ J.O. Hirshfelder, C.F. Curtis and R.B. Bird (1964). Molecular theory of gases and liquids (First ed.). Wiley. ISBN 0-471-40065-3. 
19. ^ Robert E. Maples (2000). Petroleum Refinery Process Economics (2nd ed.). Pennwell Books. ISBN 0-87814-779-9. 
20. ^ Kaatze, Udo (1995). "Fundamentals of microwaves". Radiation Physics and Chemistry 45 (4): 539–548. Bibcode 1995RaPC...45..539K. doi:10.1016/0969-806X(94)00069-V 
21. ^ "Handbook of Chemistry and Physics", 83rd edition, CRC Press, 2002.
22. ^ "Chocolate Processing". Brookfield Engineering website. http://www.brookfieldengineering.com/education/applications/laboratory-chocolate-processing.asp. Retrieved 2007-12-03. 
23. ^ ^{a b c d e f g h i j} CRC Handbook of Chemistry and Physics, 73^rd edition, 1992–1993
24. ^ Glenn Elert. "Viscosity. The Physics Hypertextbook. by Glenn Elert". Hypertextbook.com. http://hypertextbook.com/physics/matter/viscosity/. Retrieved 2010-09-14. 
25. ^ viscosity table at hyperphysics.phy-astr.gsu.edu, contains glycerin(=glycerol) viscosity
26. ^ Barbara Jacak and Peter Steinberg (May 2010). "Creating the perfect liquid in heavy-ion collisions". Physics today 63: 39. 
27. ^ Einstein (1906). A. Ann. Phys. 19: 289. 
28. ^ Guth, E., Simha, R. (1936). "Untersuchungen über die Viskosität von Suspensionen und Lösungen. 3. Über die Viskosität von Kugelsuspensionen". Kolloid Z. 74 (3): 266. doi:10.1007/BF01428643. 
29. ^ Thomas, D. G. (1965). "Transport characteristics of suspension: VIII. A note on the viscosity of Newtonian suspensions of uniform spherical particles". J. Colloid Sci. 20 (3): 267. doi:10.1016/0095-8522(65)90016-4. 
30. ^ Kitano, T., Kataoka, T., and Shirota, T. (1981). "An empirical equation of the relative viscosity of polymer melts filled with various inorganic fillers". Rheol. Acta 20 (2): 207. doi:10.1007/BF01513064. 
31. ^ Kumagai, Naoichi; Sadao Sasajima, Hidebumi Ito (15 February 1978). "Long-term Creep of Rocks: Results with Large Specimens Obtained in about 20 Years and Those with Small Specimens in about 3 Years". Journal of the Society of Materials Science (Japan) (Japan Energy Society) 27 (293): 157–161. http://translate.google.com/translate?hl=en&sl=ja&u=http://ci.nii.ac.jp/naid/110002299397/&sa=X&oi=translate&resnum=4&ct=result&prev=/search%3Fq%3DIto%2BHidebumi%26hl%3Den. Retrieved 2008-06-16. 
32. ^ Elert, Glenn. "Viscosity". The Physics Hypertextbook. http://hypertextbook.com/physics/matter/viscosity/. 
33. ^ "Antique windowpanes and the flow of supercooled liquids", by Robert C. Plumb, (Worcester Polytech. Inst., Worcester, MA, 01609, USA), J. Chem. Educ. (1989), 66 (12), 994–6
34. ^ Gibbs, Philip. "Is Glass a Liquid or a Solid?". http://math.ucr.edu/home/baez/physics/General/Glass/glass.html. Retrieved 2007-07-31. 
35. ^ Alexander Fluegel. "Viscosity calculation of glasses". Glassproperties.com. http://www.glassproperties.com/viscosity/. Retrieved 2010-09-14. 
36. ^ R.H.Doremus (2002). "Viscosity of silica". J. Appl. Phys. 92 (12): 7619–7629. Bibcode 2002JAP....92.7619D. doi:10.1063/1.1515132. 
37. ^ M.I. Ojovan and W.E. Lee (2004). "Viscosity of network liquids within Doremus approach". J. Appl. Phys. 95 (7): 3803–3810. Bibcode 2004JAP....95.3803O. doi:10.1063/1.1647260. 
38. ^ M.I. Ojovan, K.P. Travis and R.J. Hand (2000). "Thermodynamic parameters of bonds in glassy materials from viscosity-temperature relationships". J. Phys.: Condensed matter 19 (41): 415107. Bibcode 2007JPCM...19O5107O. doi:10.1088/0953-8984/19/41/415107. 
39. ^ L.D. Landau and E.M. Lifshitz (translated from Russian by J.B. Sykes and W.H. Reid) (1997). Fluid Mechanics (2nd ed.). Butterworth Heinemann. ISBN 0-7506-2767-0. 

ASTM D 2161, Standard Practice for Conversion of Kinematic Viscosity to Saybolt Universal Viscosity or to Saybolt Furol Viscosity

Further reading

• Hatschek, Emil (1928). The Viscosity of Liquids. New York: Van Nostrand. OCLC 53438464.
• Massey, B. S.; A. J. Ward-Smith (2011). Mechanics of Fluids (Ninth ed.). London; New York: Spon Press. ISBN 9780415602594,. OCLC 690084654. ISBN 9780415602600, ISBN 9780203835449. 

External links

• Fluid properties High accuracy calculation of viscosity and other physical properties of frequent used pure liquids and gases.
• Fluid Characteristics Chart A table of viscosities and vapor pressures for various fluids
• Gas Dynamics Toolbox Calculate coefficient of viscosity for mixtures of gases
• Glass Viscosity Measurement Viscosity measurement, viscosity units and fixpoints, glass viscosity calculation
• Kinematic Viscosity conversion between kinematic and dynamic viscosity.
• Physical Characteristics of Water A table of water viscosity as a function of temperature
• Vogel–Tammann–Fulcher Equation Parameters
• Calculation of temperature-dependent dynamic viscosities for some common components