- Thermodynamics
-
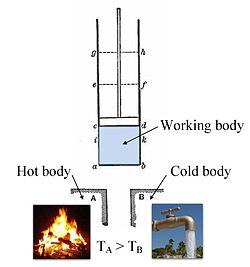 Annotated color version of the original 1824 Carnot heat engine showing the hot body (boiler), working body (system, steam), and cold body (water), the letters labeled according to the stopping points in Carnot cycle.
Annotated color version of the original 1824 Carnot heat engine showing the hot body (boiler), working body (system, steam), and cold body (water), the letters labeled according to the stopping points in Carnot cycle.
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation. It interrelates macroscopic variables, such as temperature, volume and pressure, which describe physical properties of material bodies and radiation, which in this science are called thermodynamic systems.
Historically, thermodynamics developed out of a desire to increase the efficiency of early steam engines, particularly through the work of French physicist Nicolas Léonard Sadi Carnot (1824) who believed that the efficiency of heat engines was the key that could help France win the Napoleonic Wars.[1] Scottish physicist Lord Kelvin was the first to formulate a concise definition of thermodynamics in 1854:[2]
Thermo-dynamics is the subject of the relation of heat to forces acting between contiguous parts of bodies, and the relation of heat to electrical agency.
Initially, the thermodynamics of heat engines concerned mainly the thermal properties of their 'working materials', such as steam. This concern was then linked to the study of energy transfers in chemical processes, for example to the investigation, published in 1840, of the heats of chemical reactions[3] by Germain Hess, which was not originally explicitly concerned with the relation between energy exchanges by heat and work. Chemical thermodynamics studies the role of entropy in chemical reactions.[4][5][6][7][8][9][10][11][12] Also, statistical thermodynamics, or statistical mechanics, gave explanations of macroscopic thermodynamics by statistical predictions of the collective motion of particles based on the mechanics of their microscopic behavior.
Thermodynamics describes how systems change when they interact with one another or with their surroundings. This can be applied to a wide variety of topics in science and engineering, such as engines, phase transitions, chemical reactions, transport phenomena, and even black holes. The results of thermodynamics are essential for other fields of physics and for chemistry, chemical engineering, aerospace engineering, mechanical engineering, cell biology, biomedical engineering, materials science, and are useful for other fields such as economics.[13][14]
Many of the empirical facts of thermodynamics are comprehended in its four laws. The first law specifies that energy can be exchanged between physical systems as heat and thermodynamic work.[15] The second law concerns a quantity called entropy, that expresses limitations, arising from what is known as irreversibility, on the amount of thermodynamic work that can be delivered to an external system by a thermodynamic process.[16] Many writers offer various axiomatic formulations of thermodynamics, as if it were a completed subject, but non-equilibrium processes continue to make difficulties for it.
Contents
Introduction
Thermodynamics is built on the study of energy transfers that can be strictly resolved into two distinct components, heat and work, specified by macroscopic variables.[17] Though thermodynamics originated in the study of cyclic non-equilibrium processes such as the working of heat engines, study of the subject gradually revealed that the notion of heat is inextricably tied to the notion of thermodynamic equilibrium.[18] Thermodynamics is well understood and validated for systems in thermodynamic equilibrium, but as the systems of interest become further and further from thermodynamic equilibrium, their thermodynamical study becomes more and more difficult. Systems in thermodynamic equilibrium have very well experimentally reproducible behaviour, and as interest moves further towards non-equilibrium systems, experimental reproducibility becomes more difficult. The present article takes a gradual approach to the subject, starting with a focus on cyclic processes and thermodynamic equilibrium, and then gradually beginning to further consider non-equilibrium systems.
Classical thermodynamics describes macroscopic properties of bodies. This means that "any reference to [the] atomic constitution [of matter] is foreign to classical thermodynamics" in its macroscopic sense, as distinct from classical statistical thermodynamics.[19] Here the word 'classical' is being used in a special sense, not the same as the sense 'pre-quantum' that contrasts with 'quantum'; here the word 'classical' means 'long established in physics', including both pre-quantum and quantum physics. The term 'statistical mechanics' will be clarified a little later in this article, but here it means simply that the processes in a body are considered in terms of the atomic constitution of matter.
Nevertheless, Fowler and Guggenheim observe that classical statistical thermodynamics provides a perspective from which to view the nature of classical macroscopic thermodynamics, as follows: for classical macroscopic thermodynamics and classical statistical mechanics to apply to a process in a body, it is necessary that the atomic mechanisms of the process fall into just two classes: those so fast that, in the time frame of the process or phenomenon of interest, the atomic states effectively visit all of their accessible range, and those so slow that their effects can be neglected in the time frame of the experiment or phenomenon of interest.[20] "When intermediate rates are present, [classical] thermodynamics and [classical] statistical mechanics cannot be applied."[21] This theme of separation of time scales of atomic processes recurs throughout the subject. This is a correlate of the division of transfers of energy into those as heat and those as work. This is another way of saying that non-equilibrium processes can be very much harder to study than processes that stay near equilibrium.
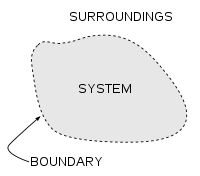
Basic for thermodynamics are the concepts of system and surroundings.[8][22]
There are two fundamental kinds of entity in thermodynamics, states of a system, and processes of a system. This allows two fundamental approaches to thermodynamic reasoning, that in terms of states of a system, and that in terms of cyclic processes of a system.
A thermodynamic system can be defined in terms of its states. In this way, a thermodynamic system is a macroscopic physical object, explicitly specified in terms of macroscopic physical and chemical variables which describe its macroscopic properties. The macroscopic state variables of thermodynamics have been recognized in the course of empirical work in physics and chemistry.[9]
A thermodynamic system can also be defined in terms of the processes which it can undergo. Of particular interest are cyclic processes. This was the way of the founders of thermodynamics in the first three quarters of the nineteenth century.
The surroundings of a thermodynamic system are other thermodynamic systems that can interact with it. An example of a thermodynamic surrounding is a heat bath, which is considered to be held at a prescribed temperature, regardless of the interactions it might have with the system.
The macroscopic variables of a thermodynamic system can under some conditions be related to one another through equations of state. They express the constitutive peculiarities of the material of the system. Classical thermodynamics is characterized by its study of materials that have equations of state that express relations between mechanical variables and temperature that are reached much more rapidly than any changes in the surroundings. A classical material can usually be described by a function that makes pressure dependent on volume and temperature, the resulting pressure being established much more rapidly than any imposed change of volume or temperature.[23]
Thermodynamic facts can often be explained by viewing macroscopic objects as assemblies of very many microscopic or atomic objects that obey Hamiltonian dynamics.[8][24][25] The microscopic or atomic objects exist in species, the objects of each species being all alike. Because of this likeness, statistical methods can be used to account for the macroscopic properties of the thermodynamic system in terms of the properties of the microscopic species. Such explanation is called statistical thermodynamics; also often it is also referred to by the term 'statistical mechanics', though this term can have a wider meaning, referring to 'microscopic objects', such as economic quantities, that do not obey Hamiltonian dynamics.[24]
 The thermodynamicists representative of the original eight founding schools of thermodynamics. The schools with the most-lasting effect in founding the modern versions of thermodynamics are the Berlin school, particularly as established in Rudolf Clausius’s 1865 textbook The Mechanical Theory of Heat, the Vienna school, with the statistical mechanics of Ludwig Boltzmann, and the Gibbsian school at Yale University, American engineer Willard Gibbs' 1876 On the Equilibrium of Heterogeneous Substances launching chemical thermodynamics.[26]
The thermodynamicists representative of the original eight founding schools of thermodynamics. The schools with the most-lasting effect in founding the modern versions of thermodynamics are the Berlin school, particularly as established in Rudolf Clausius’s 1865 textbook The Mechanical Theory of Heat, the Vienna school, with the statistical mechanics of Ludwig Boltzmann, and the Gibbsian school at Yale University, American engineer Willard Gibbs' 1876 On the Equilibrium of Heterogeneous Substances launching chemical thermodynamics.[26]
History
The history of thermodynamics as a scientific discipline generally begins with Otto von Guericke who, in 1650, built and designed the world's first vacuum pump and demonstrated a vacuum using his Magdeburg hemispheres. Guericke was driven to make a vacuum in order to disprove Aristotle's long-held supposition that 'nature abhors a vacuum'. Shortly after Guericke, the English physicist and chemist Robert Boyle had learned of Guericke's designs and, in 1656, in coordination with English scientist Robert Hooke, built an air pump.[27] Using this pump, Boyle and Hooke noticed a correlation between pressure, temperature, and volume. In time, Boyle's Law was formulated, which states that pressure and volume are inversely proportional. Then, in 1679, based on these concepts, an associate of Boyle's named Denis Papin built a steam digester, which was a closed vessel with a tightly fitting lid that confined steam until a high pressure was generated.
Later designs implemented a steam release valve that kept the machine from exploding. By watching the valve rhythmically move up and down, Papin conceived of the idea of a piston and a cylinder engine. He did not, however, follow through with his design. Nevertheless, in 1697, based on Papin's designs, engineer Thomas Savery built the first engine, followed by Thomas Newcomen in 1712. Although these early engines were crude and inefficient, they attracted the attention of the leading scientists of the time.
The fundamental concepts of heat capacity and latent heat, which were necessary for the development of thermodynamics, were developed by Professor Joseph Black at the University of Glasgow, where James Watt was employed as an instrument maker. Black and Watt performed experiments together, but it was Watt who conceived the idea of the external condenser which resulted in a large increase in steam engine efficiency.[28] Drawing on all the previous work led Sadi Carnot, the "father of thermodynamics", to publish Reflections on the Motive Power of Fire (1824), a discourse on heat, power, energy and engine efficiency. The paper outlined the basic energetic relations between the Carnot engine, the Carnot cycle, and motive power. It marked the start of thermodynamics as a modern science.[11]
The first thermodynamic textbook was written in 1859 by William Rankine, originally trained as a physicist and a civil and mechanical engineering professor at the University of Glasgow.[29] The first and second laws of thermodynamics emerged simultaneously in the 1850s, primarily out of the works of William Rankine, Rudolf Clausius, and William Thomson (Lord Kelvin).
The foundations of statistical thermodynamics were set out by physicists such as James Clerk Maxwell, Ludwig Boltzmann, Max Planck, Rudolf Clausius and J. Willard Gibbs.
During the years 1873–76 the American mathematical physicist Josiah Willard Gibbs published a series of three papers, the most famous being On the Equilibrium of Heterogeneous Substances,[4] in which he showed how thermodynamic processes, including chemical reactions, could be graphically analyzed, by studying the energy, entropy, volume, temperature and pressure of the thermodynamic system in such a manner, one can determine if a process would occur spontaneously.[30] Also Pierre Duhem in the 19th century wrote about chemical thermodynamics.[5] During the early 20th century, chemists such as Gilbert N. Lewis, Merle Randall,[6] and E. A. Guggenheim[7][8] applied the mathematical methods of Gibbs to the analysis of chemical processes.
Etymology
The etymology of thermodynamics has an intricate history.[31] It was first spelled in a hyphenated form as an adjective (thermo-dynamic) and from 1854 to 1868 as the noun thermo-dynamics to represent the science of generalized heat engines.[31]
The components of the word thermodynamics are derived from the Greek words θέρμη therme, meaning heat, and δύναμις dynamis, meaning power.[32][33][34]
Pierre Perrot claims that the term thermodynamics was coined by James Joule in 1858 to designate the science of relations between heat and power.[11] Joule, however, never used that term, but used instead the term perfect thermo-dynamic engine in reference to Thomson’s 1849[35] phraseology.[31]
By 1858, thermo-dynamics, as a functional term, was used in William Thomson's paper An Account of Carnot's Theory of the Motive Power of Heat.[35]
Branches of description
The study of thermodynamical systems has developed into several related branches, each using a different fundamental model as a theoretical or experimental basis, or applying the principles to varying types of systems.
Classical thermodynamics
Classical thermodynamics is the description of the states (especially equilibrium states) and processes of thermodynamical systems, using macroscopic, empirical properties directly measurable in the laboratory. It is used to model exchanges of energy, work, heat, and matter, based on the laws of thermodynamics. The qualifier classical reflects the fact that it represents the descriptive level in terms of macroscopic empirical parameters that can be measured in the laboratory, that was the first level of understanding in the 19th century. A microscopic interpretation of these concepts was provided by the development of statistical thermodynamics.
Statistical thermodynamics
Statistical thermodynamics, also called statistical mechanics, emerged with the development of atomic and molecular theories in the second half of the 19th century and early 20th century, supplementing thermodynamics with an interpretation of the microscopic interactions between individual particles or quantum-mechanical states. This field relates the microscopic properties of individual atoms and molecules to the macroscopic, bulk properties of materials that can be observed on the human scale, thereby explaining thermodynamics as a natural result of statistics, classical mechanics, and quantum theory at the microscopic level.
Chemical thermodynamics
Chemical thermodynamics is the study of the interrelation of energy with chemical reactions and chemical transport and with physical changes of state within the confines of the laws of thermodynamics.
Treatment of equilibrium
Equilibrium thermodynamics studies transformations of matter and energy in systems as they approach equilibrium. The equilibrium means balance. In a thermodynamic equilibrium state there is no macroscopic flow and no macroscopic change is occurring or can be triggered; within the system, every microscopic process is balanced by its opposite; this is called the principle of detailed balance. A central aim in equilibrium thermodynamics is: given a system in a well-defined initial state, subject to accurately specified constraints, to calculate what the state of the system will be once it has reached equilibrium. A thermodynamic system is said to be homogeneous when all its locally defined intensive variables are spatially invariant. A simple system in thermodynamic equilibrium is homogeneous unless it is affected by a time-invariant externally imposed field of force, such as gravity, electricity, or magnetism.
Most systems found in nature are not in thermodynamic equilibrium, exactly considered; for they are changing or can be triggered to change over time, and are continuously and discontinuously subject to flux of matter and energy to and from other systems. Nevertheless, many systems in nature are nearly enough in thermodynamic equilibrium that for many purposes their behaviour can be nearly enough approximated by equilibrium calculations.
For their thermodynamic study, systems that are further from thermodynamic equilibrium call for more general ideas. Non-equilibrium thermodynamics is a branch of thermodynamics that deals with systems that are not in thermodynamic equilibrium. Non-equilibrium thermodynamics is distinct because it is concerned with transport processes and with the rates of chemical reactions.[36] Non-equilibrium systems can be in stationary states that are not homogeneous even when there is no externally imposed field of force; in this case, the description of the internal state of the system requires a field theory.[37][38][39] Many natural systems still today remain beyond the scope of currently known macroscopic thermodynamic methods.
Laws of thermodynamics
Thermodynamics states a set of four laws which are valid for all systems that fall within the constraints implied by each. In the various theoretical descriptions of thermodynamics these laws may be expressed in seemingly differing forms, but the most prominent formulations are the following:
- Zeroth law of thermodynamics: If two systems are each in thermal equilibrium with a third, they are also in thermal equilibrium with each other.
This statement implies that thermal equilibrium is an equivalence relation on the set of thermodynamic systems under consideration. Systems are said to be in equilibrium if the small, random exchanges between them (e.g. Brownian motion) do not lead to a net change in energy. This law is tacitly assumed in every measurement of temperature. Thus, if one seeks to decide if two bodies are at the same temperature, it is not necessary to bring them into contact and measure any changes of their observable properties in time.[40] The law provides an empirical definition of temperature and justification for the construction of practical thermometers.
The zeroth law was not initially recognized as a law, as its basis in thermodynamical equilibrium was implied in the other laws. The first, second, and third laws had been explicitly stated prior and found common acceptance in the physics community. Once the importance of the zeroth law for the definition of temperature was realized, it was impracticable to renumber the other laws, hence it was numbered the zeroth law.
- First law of thermodynamics: A change in the internal energy of a closed thermodynamic system is equal to the difference between the heat supplied to the system and the amount of work done by the system on its surroundings.[41][42][43][44][45][46][47][48][49][50]
The first law of thermodynamics asserts the existence of a state variable for a system, the internal energy, and tells how it changes in thermodynamic processes. The law allows a given internal energy of a system to be reached by any combination of heat and work. It is important that internal energy is a variable of state of the system (see Thermodynamic state) whereas heat and work change the state of the system.
The first law observes that the internal energy obeys the principle of conservation of energy, which states that energy can be transformed (changed from one form to another), but cannot be created or destroyed.[51]
- Second law of thermodynamics: Heat cannot spontaneously flow from a colder location to a hotter location.
The second law of thermodynamics is an expression of the universal principle of decay observable in nature. The second law is an observation of the fact that over time, differences in temperature, pressure, and chemical potential tend to even out in a physical system that is isolated from the outside world. Entropy is a measure of how much this process has progressed. The entropy of an isolated system which is not in equilibrium will tend to increase over time, approaching a maximum value at equilibrium.
In classical thermodynamics, the second law is a basic postulate applicable to any system involving heat energy transfer; in statistical thermodynamics, the second law is a consequence of the assumed randomness of molecular chaos. There are many versions of the second law, but they all have the same effect, which is to explain the phenomenon of irreversibility in nature.
- Third law of thermodynamics: As a system approaches absolute zero, all processes cease and the entropy of the system approaches a minimum value.
The third law of thermodynamics is a statistical law of nature regarding entropy and the impossibility of reaching absolute zero of temperature. This law provides an absolute reference point for the determination of entropy. The entropy determined relative to this point is the absolute entropy. Alternate definitions are, "the entropy of all systems and of all states of a system is smallest at absolute zero," or equivalently "it is impossible to reach the absolute zero of temperature by any finite number of processes".
Absolute zero, at which all activity (with the exception of that caused by zero point energy) would stop is −273.15 °C (degrees Celsius), or −459.67 °F (degrees Fahrenheit) or 0 K (kelvin).
System models
An important concept in thermodynamics is the thermodynamic system, a precisely defined region of the universe under study. Everything in the universe except the system is known as the surroundings. A system is separated from the remainder of the universe by a boundary which may be notional or not, but which by convention delimits a finite volume. Exchanges of work, heat, or matter between the system and the surroundings take place across this boundary.
In practice, the boundary is simply an imaginary dotted line drawn around a volume when there is going to be a change in the internal energy of that volume. Anything that passes across the boundary that effects a change in the internal energy needs to be accounted for in the energy balance equation. The volume can be the region surrounding a single atom resonating energy, such as Max Planck defined in 1900; it can be a body of steam or air in a steam engine, such as Sadi Carnot defined in 1824; it can be the body of a tropical cyclone, such as Kerry Emanuel theorized in 1986 in the field of atmospheric thermodynamics; it could also be just one nuclide (i.e. a system of quarks) as hypothesized in quantum thermodynamics.
Boundaries are of four types: fixed, moveable, real, and imaginary. For example, in an engine, a fixed boundary means the piston is locked at its position; as such, a constant volume process occurs. In that same engine, a moveable boundary allows the piston to move in and out. For closed systems, boundaries are real while for open system boundaries are often imaginary.
Generally, thermodynamics distinguishes three classes of systems, defined in terms of what is allowed to cross their boundaries:
Interactions of thermodynamic systems Type of system Mass flow Work Heat Open 


Closed 


Isolated 


As time passes in an isolated system, internal differences in the system tend to even out and pressures and temperatures tend to equalize, as do density differences. A system in which all equalizing processes have gone to completion is considered to be in a state of thermodynamic equilibrium.
In thermodynamic equilibrium, a system's properties are, by definition, unchanging in time. Systems in equilibrium are much simpler and easier to understand than systems which are not in equilibrium. Often, when analyzing a thermodynamic process, it can be assumed that each intermediate state in the process is at equilibrium. This will also considerably simplify the situation. Thermodynamic processes which develop so slowly as to allow each intermediate step to be an equilibrium state are said to be reversible processes.
States and processes
There are two fundamental kinds of entity in thermodynamics, states of a system, and processes of a system. This allows two fundamental approaches to thermodynamic reasoning, that in terms of states of a system, and that in terms of cyclic processes of a system.
The approach through states of a system requires a full account of the state of the system as well as a notion of process from one state to another of a system, but may require only a partial account of the state of the surroundings of the system or of other systems.
The notion of a cyclic process does not require a full account of the state of the system, but does require a full account of how the process occasions transfers of matter and energy between the system and its surroundings, which must include at least two heat reservoirs at different temperatures, one hotter than the other. In this approach, the notion of a properly numerical scale of temperature is a presupposition of thermodynamics, not a notion constructed by or derived from it.
Thermodynamic state variables
When a system is at thermodynamic equilibrium under a given set of conditions of its surroundings, it is said to be in a definite thermodynamic state, which is fully described by its state variables.
Thermodynamic state variables are of two kinds, extensive and intensive.[8][24] Examples of extensive thermodynamic variables are total mass and total volume. Examples of intensive thermodynamic variables are temperature, pressure, and chemical concentration; intensive thermodynamic variables are defined at each spatial point and each instant of time in a system. Physical macroscopic variables can be mechanical or thermal.[24] Temperature is a thermal variable; according to Guggenheim, "the most important conception in thermodynamics is temperature."[8]
If a system is in thermodynamic equilibrium and is not subject to an externally imposed force field, such as gravity, electricity, or magnetism, then (subject to a proviso stated in the following sentence) it is homogeneous, that is say, spatially uniform in all respects.[52] There is a proviso here; a system in thermodynamic equilibrium can be inhomogeneous in the following respect: it can consist of several so-called 'phases', each homogeneous in itself, in immediate contiguity with other phases of the system, but distinguishable by their having various respectively different physical characters; a mixture of different chemical species is considered homogeneous for this purpose if it is physically homogeneous.[53] For example, a vessel can contain a system consisting of water vapour overlying liquid water; then there is a vapour phase and a liquid phase, each homogeneous in itself, but still in thermodynamic equilibrium with the other phase. For the immediately present account, systems with multiple phases are not considered, though for many thermodynamic questions, multiphase systems are important.
In a sense, a homogeneous system can be regarded as spatially zero-dimensional, because it has no spatial variation.
If a system in thermodynamic equilibrium is homogeneous, then its state can be described by a number of intensive variables and extensive variables.[39][54][55]
Intensive variables are defined by the property that if any number of systems, each in its own separate homogeneous thermodynamic equilibrium state, all with the same respective values of all of their intensive variables, regardless of the values of their extensive variables, are laid contiguously with no partition between them, so as to form a new system, then the values of the intensive variables of the new system are the same as those of the separate constituent systems. Such a composite system is in a homogeneous thermodynamic equilibrium. Examples of intensive variables are temperature, chemical concentration, pressure, density of mass, density of internal energy, and, when it can be properly defined, density of entropy.[56]
Extensive variables are defined by the property that if any number of systems, regardless of their possible separate thermodynamic equilibrium or non-equilibrium states or intensive variables, are laid side by side with no partition between them so as to form a new system, then the values of the extensive variables of the new system are the sums of the values of the respective extensive variables of the individual separate constituent systems. Obviously, there is no reason to expect such a composite system to be in in a homogeneous thermodynamic equilibrium. Examples of extensive variables are mass, volume, and internal energy. They depend on the total quantity of mass in the system.[57]
Though, when it can be properly defined, density of entropy is an intensive variable, entropy itself does not fit into this classification of state variables.[58] The reason is that entropy is a property of a system as a whole, and not necessarily related simply to its constituents separately. It is true that for any number of systems each in its own separate homogeneous thermodynamic equilibrium, all with the same values of intensive variables, removal of the partitions between the separate systems results in a composite homogeneous system in thermodynamic equilibrium, with all the values of its intensive variables the same as those of the constituent systems, and it is reservedly or conditionally true that the entropy of such a restrictively defined composite system is the sum of the entropies of the constituent systems. But if the constituent systems do not satisfy these restrictive conditions, the entropy of a composite system cannot be expected to be the sum of the entropies of the constituent systems, because the entropy is a property of the composite system as a whole. Therefore, though under these restrictive reservations, entropy satisfies some requirements for extensivity defined just above, entropy in general does not fit the above definition of an extensive variable.
Being neither an intensive variable nor an extensive variable according to the above definition, entropy is thus a stand-out variable, because it is a state variable of a system as a whole.[58] A non-equilibrium system can have a very inhomogeneous dynamical structure. This is one reason for distinguishing the study of equilibrium thermodynamics from the study of non-equilibrium thermodynamics.
The physical reason for the existence of extensive variables is the time-invariance of volume in a given inertial reference frame, and the strictly local conservation of mass, momentum, angular momentum, and energy. As noted by Gibbs, entropy is unlike energy and mass, because it is not locally conserved.[58] The stand-out quantity entropy is never conserved in real physical processes; all real physical processes are irreversible.[59] The motion of planets seems reversible on a short time scale (millions of years), but their motion, according to Newton's laws, is mathematically an example of deterministic chaos. Eventually a planet will suffer an unpredictable collision with an object from its surroundings, outer space in this case, and consequently its future course will be radically unpredictable. Theoretically this can be expressed by saying that every natural process dissipates some information from the predictable part of its activity into the unpredictable part. The predictable part is expressed in the generalized mechanical variables, and the unpredictable part in heat.
There are other state variables which can be regarded as conditionally 'extensive' subject to reservation as above, but not extensive as defined above. Examples are the Gibbs free energy, the Helmholtz free energy, and the enthalpy. Consequently, just because for some systems under particular conditions of their surroundings such state variables are conditionally conjugate to intensive variables, such conjugacy does not make such state variables extensive as defined above. This is another reason for distinguishing the study of equilibrium thermodynamics from the study of non-equilibrium thermodynamics. In another way of thinking, this explains why heat is to be regarded as a quantity that refers to a process and not to a state of a system.
Equation of state
The properties of a system can under some conditions be described by an equation of state which specifies the relationship between state variables. The equation of state expresses constitutive properties of the material of the system. It must comply with some thermodynamic constraints, but cannot be derived from the general principles of thermodynamics alone.
Thermodynamic processes
A thermodynamic process is defined by changes of state internal to the system of interest, combined with transfers of matter and energy to and from the surroundings of the system or to and from other systems. A system is demarcated from its surroundings or from other systems by partitions which may more or less separate them, and may move as a piston to change the volume of the system and thus transfer work.
Dependent and independent variables for a process
A process is described by changes in values of state variables of systems or by quantities of exchange of matter and energy between systems and surroundings. The change must be specified in terms of prescribed variables. The choice of which variables are to be used is made in advance of consideration of the course of the process, and cannot be changed. Certain of the variables chosen in advance are called the independent variables.[60] From changes in independent variables may be derived changes in other variables called dependent variables. For example a process may occur at constant pressure with pressure prescribed as an independent variable, and temperature changed as another independent variable, and then changes in volume are considered as dependent. Careful attention to this principle is necessary in thermodynamics.[61][62]
Changes of state of a system
In the approach through states of the system, a process can be described in two main ways.
In one way, the system is considered to be connected to the surroundings by some kind of more or less separating partition, and allowed to reach equilibrium with the surroundings with that partition in place. Then, while the separative character of the partition is kept unchanged, the conditions of the surroundings are changed, and exert their influence on the system again through the separating partition, or the partition is moved so as to change the volume of the system; and a new equilibrium is reached. For example, a system is allowed to reach equilibrium with a heat bath at one temperature; then the temperature of the heat bath is changed and the system is allowed to reach a new equilibrium; if the partition allows conduction of heat, the new equilibrium will be different from the old equilibrium.
In the other way, several systems are connected to one another by various kinds of more or less separating partitions, and to reach equilibrium with each other, with those partitions in place. In this way, one may speak of a 'compound system'. Then one or more partitions is removed or changed in its separative properties or moved, and a new equilibrium is reached. The Joule-Thomson experiment is an example of this; a tube of gas is separated from another tube by a porous partition; the volume available in each of the tubes is determined by respective pistons; equilibrium is established with an initial set of volumes; the volumes are changed and a new equilibrium is established.[63][64][65][66][67] Another example is in separation and mixing of gases, with use of chemically semi-permeable membranes.[68]
Cyclic processes
A cyclic process[69] is a process that can be repeated indefinitely often without changing the final state of the system in which the process occurs. The only traces of the effects of a cyclic process are to be found in the surroundings of the system or in other systems. This is the kind of process that concerned early thermodynamicists such as Carnot, and in terms of which Kelvin defined absolute temperature,[70][71] before the use of the quantity of entropy by Rankine[72] and its clear identification by Clausius.[73] For some systems, for example with some plastic working substances, cyclic processes are practically nearly unfeasible because the working substance undergoes practically irreversible changes.[38] This is why mechanical devices are lubricated with oil and one of the reasons why electrical devices are often useful.
A cyclic process of a system requires in its surroundings at least two heat reservoirs at different temperatures, one at a higher temperature that supplies heat to the system, the other at a lower temperature that accepts heat from the system. The early work on thermodynamics tended to use the cyclic process approach, because it was interested in machines which would convert some of the heat from the surroundings into mechanical power delivered to the surroundings, without too much concern about the internal workings of the machine. Such a machine, while receiving an amount of heat from a higher temperature reservoir, always needs a lower temperature reservoir that accepts some lesser amount of heat, the difference in amounts of heat being converted to work.[74][75] Later, the internal workings of a system became of interest, and they are described by the states of the system. Nowadays, instead of arguing in terms of cyclic processes, some writers are inclined to derive the concept of absolute temperature from the concept of entropy, a variable of state.
Commonly considered thermodynamic processes
It is often convenient to study a thermodynamic process in which a single variable, such as temperature, pressure, or volume, etc., is held fixed. Furthermore, it is useful to group these processes into pairs, in which each variable held constant is one member of a conjugate pair.
Several commonly studied thermodynamic processes are:
- Isobaric process: occurs at constant pressure
- Isochoric process: occurs at constant volume (also called isometric/isovolumetric)
- Isothermal process: occurs at a constant temperature
- Adiabatic process: occurs without loss or gain of energy by heat
- Isentropic process: a reversible adiabatic process, occurs at a constant entropy
- Isenthalpic process: occurs at a constant enthalpy
- Isolated process: occurs at constant internal energy and elementary chemical composition
It is sometimes of interest to study a process in which several variables are controlled, subject to some specified constraint. In a system in which a chemical reaction can occur, for example, in which the pressure and temperature can affect the equilibrium composition, a process might occur in which temperature is held constant but pressure is slowly altered, just so that chemical equilibrium is maintained all the way. There will be a corresponding process at constant temperature in which the final pressure is the same but is reached by a rapid jump. Then it can be shown that the volume change resulting from the rapid jump process is smaller than that from the slow equilibrium process.[76] The work transferred differs between the two processes.
Instrumentation
There are two types of thermodynamic instruments, the meter and the reservoir. A thermodynamic meter is any device which measures any parameter of a thermodynamic system. In some cases, the thermodynamic parameter is actually defined in terms of an idealized measuring instrument. For example, the zeroth law states that if two bodies are in thermal equilibrium with a third body, they are also in thermal equilibrium with each other. This principle, as noted by James Maxwell in 1872, asserts that it is possible to measure temperature. An idealized thermometer is a sample of an ideal gas at constant pressure. From the ideal gas law PV=nRT, the volume of such a sample can be used as an indicator of temperature; in this manner it defines temperature. Although pressure is defined mechanically, a pressure-measuring device, called a barometer may also be constructed from a sample of an ideal gas held at a constant temperature. A calorimeter is a device which is used to measure and define the internal energy of a system.
A thermodynamic reservoir is a system which is so large that it does not appreciably alter its state parameters when brought into contact with the test system. It is used to impose a particular value of a state parameter upon the system. For example, a pressure reservoir is a system at a particular pressure, which imposes that pressure upon any test system that it is mechanically connected to. The Earth's atmosphere is often used as a pressure reservoir.
Conjugate variables
A central concept of thermodynamics is that of energy. By the First Law, the total energy of a system and its surroundings is conserved. Energy may be transferred into a system by heating, compression, or addition of matter, and extracted from a system by cooling, expansion, or extraction of matter. In mechanics, for example, energy transfer equals the product of the force applied to a body and the resulting displacement.
Conjugate variables are pairs of thermodynamic concepts, with the first being akin to a "force" applied to some thermodynamic system, the second being akin to the resulting "displacement," and the product of the two equalling the amount of energy transferred. The common conjugate variables are:
- Pressure-volume (the mechanical parameters);
- Temperature-entropy (thermal parameters);
- Chemical potential-particle number (material parameters).
Potentials
Thermodynamic potentials are different quantitative measures of the stored energy in a system. Potentials are used to measure energy changes in systems as they evolve from an initial state to a final state. The potential used depends on the constraints of the system, such as constant temperature or pressure. For example, the Helmholtz and Gibbs energies are the energies available in a system to do useful work when the temperature and volume or the pressure and temperature are fixed, respectively.
The five most well known potentials are:
Name Symbol Formula Natural variables Internal energy U 
S,V,{Ni} Helmholtz free energy F U − TS T,V,{Ni} Enthalpy H U + pV S,p,{Ni} Gibbs free energy G U + pV − TS T,p,{Ni} Landau Potential (Grand potential) Ω, ΦG U − TS −  μiNi
μiNiT,V,{μi} where T is the temperature, S the entropy, p the pressure, V the volume, μ the chemical potential, N the number of particles in the system, and i is the count of particles types in the system.
Thermodynamic potentials can be derived from the energy balance equation applied to a thermodynamic system. Other thermodynamic potentials can also be obtained through Legendre transformation.
Axiomatics
Most accounts of thermodynamics presuppose the law of conservation of mass, sometimes with,[77] and sometimes without,[78][79][22] explicit mention. Particular attention is paid to the law in accounts of non-equilibrium thermodynamics.[80][81] One statement of this law is "The total mass of [a closed] system remains constant."[9] Another statement of it is "In a chemical reaction, matter is neither created nor destroyed."[82] Implied in this is that matter and energy are not considered to be interconverted in such accounts. The full generality of the law of conservation of energy is thus not used in such accounts.
In 1909, Constantin Carathéodory presented[83] a purely mathematical axiomatic formulation, a description often referred to as geometrical thermodynamics, and sometimes said to take the "mechanical approach"[49] to thermodynamics. The Carathéodory formulation is restricted to equilibrium thermodynamics and does not attempt to deal with non-equilibrium thermodynamics, forces that act at a distance on the system, or surface tension effects.[84] Moreover, Carathéodory's formulation does not deal with materials like water near 4C, which have a density extremum as a function of temperature at constant pressure.[85][86] Carathéodory used the law of conservation of energy as an axiom from which, along with the contents of the zeroth law, and some other assumptions including his own version of the second law, he derived the first law of thermodynamics.[87] Consequently one might also describe Carathėodory's work as lying in the field of energetics,[88] which is broader than thermodynamics. Carathéodory presupposed the law of conservation of mass without explicit mention of it.
Since the time of Carathėodory, other influential axiomatic formulations of thermodynamics have appeared, which like Carathéodory's, use their own respective axioms, different from the usual statements of the four laws, to derive the four usually stated laws.[89][90][91]
Many axiomatic developments assume the existence of states of thermodynamic equilibrium and of states of thermal equilibrium. States of thermodynamic equilibrium of compound systems allow their component simple systems to exchange heat and matter and to do work on each other on their way to overall joint equilibrium. Thermal equilibrium allows them only to exchange heat. The physical properties of glass depend on its history of being heated and cooled and, strictly speaking, glass is not in thermodynamic equilibrium.[92]
According to Herbert Callen's widely cited 1985 text on thermodynamics: "An essential prerequisite for the measurability of energy is the existence of walls that do not permit transfer of energy in the form of heat."[93]. According to Werner Heisenberg's mature and careful examination of the basic concepts of physics, the theory of heat has a self-standing place.[94]
From the viewpoint of the axiomatist, there are several different ways of thinking about heat, temperature, and the second law of thermodynamics. The Clausius way rests on the empirical fact that heat is conducted always down, never up, a temperature gradient. The Kelvin way is to assert the empirical fact that conversion of heat into work by cyclic processes is never perfectly efficient. A more mathematical way is to assert the existence of a function of state called the entropy which tells whether a hypothesized process will occur spontanteously in nature. A more abstract way is that of Carathéodory that in effect asserts the irreversibility of some adiabatic processes. For these different ways, there are respective corresponding different ways of viewing heat and temperature.
The Clausius-Kelvin-Planck way This way prefers ideas close to the empirical origins of thermodynamics. It presupposes transfer of energy as heat, and empirical temperature as a scalar function of state. According to Gislason and Craig (2005): "Most thermodynamic data come from calorimetry..."[95] According to Kondepudi (2008): "Calorimetry is widely used in present day laboratories."[96] In this approach, what is often currently called the zeroth law of thermodynamics is deduced as a simple consequence of the presupposition of the nature of heat and empirical temperature, but it is not named as a numbered law of thermodynamics. Planck attributed this point of view to Clausius, Kelvin, and Maxwell. Planck wrote (on page 90 of the seventh edition, dated 1922, of his treatise) that he thought that no proof of the second law of thermodynamics could ever work that was not based on the impossibility of a perpetual motion machine of the second kind. In that treatise, Planck makes no mention of the 1909 Carathéodory way, which was well-known by 1922. Planck for himself chose a version of what is just above called the Kelvin way.[97] The development by Truesdell and Bharatha (1977) is so constructed that it can deal naturally with cases like that of water near 4C.[90]
The way that assumes the existence of entropy as a function of state This way also presupposes transfer of energy as heat, and it presupposes the usually stated form of the zeroth law of thermodynamics, and from these two it deduces the existence of empirical temperature. Then from the existence of entropy it deduces the existence of absolute thermodynamic temperature.[89][8]
The Carathéodory way This way presupposes that the state of a simple one-phase system is fully specifiable by just one more state variable than the known exhaustive list of mechanical variables of state. It does not explicitly name empirical temperature, but speaks of the one-dimensional "non-deformation coordinate". This satisfies the definition of an empirical temperature, that lies on a one-dimensional manifold. The Carathéodory way needs to assume moreover that the one-dimensional manifold has a definite sense, which determines the direction of irreversible adiabatic process, which is effectively assuming that heat is conducted from hot to cold. This way presupposes the often currently stated version of the zeroth law, but does not actually name it as one of its axioms.[84]
Scope of thermodynamics
Originally thermodynamics concerned material and radiative phenomena that are experimentally reproducible. For example, a state of thermodynamic equilibrium is a steady state reached after a system has aged so that it no longer changes with the passage of time. But more than that, for thermodynamics, a system, defined by its being prepared in a certain way must, consequent on every particular occasion of preparation, upon aging, reach one and the same eventual state of thermodynamic equilibrium, entirely determined by the way of preparation. Such reproducibility is because the systems consist of so many molecules that the molecular variations between particular occasions of preparation have negligible or scarcely discernable effects on the macroscopic variables that are used in thermodynamic descriptions. This led to Boltzmann's discovery that entropy had a statistical or probabilistic nature. Probabilistic and statistical explanations arise from the experimental reproducibility of the phenomena.[98]
Gradually, the laws of thermodynamics came to be used to explain phenomena that occur outside the experimental laboratory. For example, phenomena on the scale of the earth's atmosphere cannot be reproduced in a laboratory experiment. But processes in the atmosphere can be modeled by use of thermodynamic ideas, extended well beyond the scope of laboratory equilibrium thermodynamics.[99][100][101] A parcel of air can, near enough for many studies, be considered as a closed thermodynamic system, one that is allowed to move over significant distances. The pressure exerted by the surrounding air on the lower face of a parcel of air may differ from that on its upper face. If this results in rising of the parcel of air, it can be considered to have gained potential energy as a result of work being done on it by the combined surrounding air below and above it. As it rises, such a parcel will usually expand because the pressure is lower at the higher altitudes that it reaches. In that way, the rising parcel also does work on the surrounding atmosphere. For many studies, such a parcel can be considered nearly to neither gain nor lose energy by heat conduction to its surrounding atmosphere, and its rise is rapid enough to leave negligible time for it to gain or lose heat by radiation; consequently the rising of the parcel is near enough adiabatic. Thus the adiabatic gas law accounts for its internal state variables, provided that there is no precipitation into water droplets, no evaporation of water droplets, and no sublimation in the process. More precisely, the rising of the parcel is likely to occasion friction and turbulence, so that some potential and some kinetic energy of bulk will be converted into internal energy of air considered as effectively stationary. Friction and turbulence thus oppose the rising of the parcel.[102][103]
Applied fields
- Atmospheric thermodynamics
- Biological thermodynamics
- Black hole thermodynamics
- Chemical thermodynamics
- Classical thermodynamics
- Equilibrium thermodynamics
- Geology
- Industrial ecology (re: Exergy)
- Maximum entropy thermodynamics
- Non-equilibrium thermodynamics
- Philosophy of thermal and statistical physics
- Psychrometrics
- Quantum thermodynamics
- Statistical thermodynamics
- Thermoeconomics
See also
Lists and timelines
- List of important publications in thermodynamics
- List of textbooks in statistical mechanics
- List of thermal conductivities
- List of thermodynamic properties
- Table of thermodynamic equations
- Timeline of thermodynamics
Wikibooks
References
Books
- Callen, H.B. (1960/1985). Thermodynamics and an Introduction to Thermostatistics, (1st edition 1960) 2nd edition 1985, Wiley, New York, ISBN 9812-53-185-8.
- Fowler, R., Guggenheim, E.A. (1939). Statistical Thermodynamics, Cambridge University Press, Canbridge UK.
- Guggenheim, E.A. (1949/1967). Thermodynamics. An Advanced Treatment for Chemists and Physicists, (1st edition 1949) 5th edition 1967, North-Holland, Amsterdam.
- Planck, M. (1897/1903). Treatise on Thermodynamics, translated by A. Ogg, Longmans, Green & Co., London, [5].
- Planck, M. (1923/1926). Treatise on Thermodynamics, third English edition translated by A. Ogg from the seventh German edition, Longmans, Green & Co., London.
- Sommerfeld, A. (1952/1956). Thermodynamics and Statistical Mechanics, Academic Press, New York.
Citations
- ^ Clausius, Rudolf (1850). On the Motive Power of Heat, and on the Laws which can be deduced from it for the Theory of Heat. Poggendorff's Annalen der Physik, LXXIX (Dover Reprint). ISBN 0-486-59065-8.
- ^ Sir William Thomson, LL.D. D.C.L., F.R.S. (1882). Mathematical and Physical Papers. 1. London, Cambridge: C.J. Clay, M.A. & Son, Cambridge University Press. p. 232. http://books.google.com/books?id=nWMSAAAAIAAJ&pg=PA100&dq=On+an+Absolute+Thermometric+Scale+Founded+on+Carnot%E2%80%99s+Theory#v=onepage&q=On%20an%20Absolute%20Thermometric%20Scale%20Founded%20on%20Carnot%E2%80%99s%20Theory&f=false.
- ^ Hess, H. (1840). Thermochemische Untersuchungen, Annalen der Physik und Chemie (Poggendorff, Leipzig) 126(6): 385–404 [1].
- ^ a b Gibbs, Willard, J. (1876). Transactions of the Connecticut Academy, III, pp. 108–248, Oct. 1875 – May 1876, and pp. 343–524, May 1877 – July 1878.
- ^ a b Duhem, P.M.M. (1886). Le Potential Thermodynamique et ses Applications, Hermann, Paris.
- ^ a b Lewis, Gilbert N.; Randall, Merle (1923). Thermodynamics and the Free Energy of Chemical Substances. McGraw-Hill Book Co. Inc..
- ^ a b Guggenheim, E.A. (1933). Modern Thermodynamics by the Methods of J.W. Gibbs, Methuen, London.
- ^ a b c d e f g Guggenheim, E.A. (1949/1967)
- ^ a b c Ilya Prigogine, I. & Defay, R., translated by D.H. Everett (1954). Chemical Thermodynamics. Longmans, Green & Co., London. Includes classical non-equilibrium thermodynamics..
- ^ Enrico Fermi (1956). Thermodynamics. Courier Dover Publications. pp. (ix). ISBN 048660361X. OCLC 54033021 230763036 54033021. http://books.google.com/?id=VEZ1ljsT3IwC&printsec=frontcover&dq=thermodynamics.
- ^ a b c Perrot, Pierre (1998). A to Z of Thermodynamics. Oxford University Press. ISBN 0-19-856552-6. OCLC 38073404 123283342 38073404.
- ^ Clark, John, O.E. (2004). The Essential Dictionary of Science. Barnes & Noble Books. ISBN 0-7607-4616-8. OCLC 63473130 58732844 63473130.
- ^ Smith, J.M.; Van Ness, H.C., Abbott, M.M. (2005). Introduction to Chemical Engineering Thermodynamics. McGraw Hill. ISBN 0-07-310445-0. OCLC 56491111.
- ^ Haynie, Donald, T. (2001). Biological Thermodynamics. Cambridge University Press. ISBN 0-521-79549-4. OCLC 43993556.
- ^ Van Ness, H.C. (1983) [1969]. Understanding Thermodynamics. Dover Publications, Inc.. ISBN 9780486632773. OCLC 8846081.
- ^ Dugdale, J.S. (1998). Entropy and its Physical Meaning. Taylor and Francis. ISBN 0-7484-0569-0. OCLC 36457809.
- ^ Bridgman, P.W. (1943). The Nature of Thermodynamics, Harvard University Press, Cambridge MA, page 48.
- ^ Callen, H.B. (1960/1985), page 283.
- ^ Fowler, R., Guggenheim, E.A. (1939), page 3.
- ^ Fowler, R., Guggenheim, E.A. (1939), page 13.
- ^ Fowler, R., Guggenheim, E.A. (1939), page 13.
- ^ a b Kondepudi, D. (2008). Introduction to Modern Thermodynamics, Wiley, Chichester, ISBN 978-0-470-01598-8. Includes classical non-equilibrium thermodynamics.
- ^ Truesdell, C. (1984). Rational Thermodynamics, second edition, Springer, New York, ISBN 0-387-90874-9.
- ^ a b c d Balescu, R. (1975). Equilibrium and Nonequilibrium Statistical Mechanics, Wiley-Interscience, New York, ISBN 0-471-04600-0.
- ^ Schrödinger, E. (1946/1967). Statistical Thermodynamics. A Course of Seminar Lectures, Cambridge University Press, Cambridge UK.
- ^ Schools of thermodynamics – EoHT.info.
- ^ Partington, J.R. (1989). A Short History of Chemistry. Dover. OCLC 19353301.
- ^ The Newcomen engine was improved from 1711 until Watt's work, making the efficiency comparison subject to qualification, but the increase from the 1865 version was on the order of 100%.
- ^ Cengel, Yunus A.; Boles, Michael A. (2005). Thermodynamics – an Engineering Approach. McGraw-Hill. ISBN 0-07-310768-9.
- ^ Gibbs, Willard (1993). The Scientific Papers of J. Willard Gibbs, Volume One: Thermodynamics. Ox Bow Press. ISBN 0-918024-77-3. OCLC 27974820.
- ^ a b c "Thermodynamics (etymology)". EoHT.info. http://www.eoht.info/page/Thermo-dynamics.
- ^ Oxford English Dictionary, Oxford University Press, Oxford UK, [2].
- ^ Liddell, H.G., Scott, R. (1843/1940/1978). A Greek-English Lexicon, revised and augmented by Jones, Sir H.S., with a supplement 1968, reprinted 1978, Oxford University Press, Oxford UK, ISBN 0-19-864214-8, pages 794, 452.[3]
- ^ Donald T. Haynie (2008). Biological Thermodynamics (2 ed.). Cambridge University Press. p. 26.
- ^ a b Kelvin, William T. (1849) "An Account of Carnot's Theory of the Motive Power of Heat – with Numerical Results Deduced from Regnault's Experiments on Steam." Transactions of the Edinburg Royal Society, XVI. January 2.Scanned Copy
- ^ Fowler, R., Guggenheim, E.A. (1939), page vii.
- ^ Gyarmati, I. (1967/1970) Non-equilibrium Thermodynamics. Field Theory and Variational Principles, translated by E. Gyarmati and W.F. Heinz, Springer, New York, pages 4–14. Includes classical non-equilibrium thermodynamics.
- ^ a b Ziegler, H., (1983). An Introduction to Thermomechanics, North-Holland, Amsterdam, ISBN 0444865039
- ^ a b Balescu, R. (1975). Equilibrium and Non-equilibrium Statistical Mechanics, Wiley-Interscience, New York, ISBN 0-471-04600-0, Section 3.2, pages 64–72.
- ^ Moran, Michael J. and Howard N. Shapiro, 2008. Fundamentals of Engineering Thermodynamics. 6th ed. Wiley and Sons: 16.
- ^ Clausius, R. (1850). Ueber de bewegende Kraft der Wärme und die Gesetze, welche sich daraus für de Wärmelehre selbst ableiten lassen, Annalen der Physik und Chemie, 155 (3): 368–394.
- ^ Rankine, W.J.M. (1850). On the mechanical action of heat, especially in gases and vapours. Trans. Roy. Soc. Edinburgh, 20: 147–190.[4]
- ^ Helmholtz, H. von. (1897/1903). Vorlesungen über Theorie der Wärme, edited by F. Richarz, Press of Johann Ambrosius Barth, Leipzig, Section 46, pages 176–182, in German.
- ^ Planck, M. (1897/1903), page 43.
- ^ Guggenheim, E.A. (1949/1967), page 10.
- ^ Sommerfeld, A. (1952/1956), Section 4 A, pages 13–16.
- ^ Ilya Prigogine, I. & Defay, R., translated by D.H. Everett (1954). Chemical Thermodynamics. Longmans, Green & Co., London, page 21..
- ^ Lewis, G.N., Randall, M. (1961). Thermodynamics, second edition revised by K.S. Pitzer and L. Brewer, McGraw-Hill, New York, page 35.
- ^ a b Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics Press, New York, ISBN 0-88318-797-3, page 79.
- ^ Kondepudi, D. (2008). Introduction to Modern Thermodynamics, Wiley, Chichester, ISBN 978-0-470-01598-8, page 59.
- ^ "Energy Rules! Energy Conversion and the Laws of Thermodynamics – More About the First and Second Laws". Uwsp.edu. http://www.uwsp.edu/cnr/wcee/keep/mod1/rules/ThermoLaws.htm. Retrieved 2010-09-12.
- ^ Guggenheim, E.A. (1949/1967), page 6.
- ^ Planck, M. (1897/1903), page 65.
- ^ Ilya Prigogine, I. & Defay, R., translated by D.H. Everett (1954). Chemical Thermodynamics. Longmans, Green & Co., London, pages 1–6..
- ^ Lavenda, B.H. (1978). Thermodynamics of Irreversible Processes, Macmillan, London, ISBN 0-333-21616-4, page 12.
- ^ Guggenheim, E.A. (1949/1967), page 19.
- ^ Guggenheim, E.A. (1949/1967), pages 18–19.
- ^ a b c Grandy, W.T., Jr (2008). Entropy and the Time Evolution of Macroscopic Systems, Oxford University Press, Oxford, ISBN 978-0-19-954617-6, Chapter 5, pages 59–68.
- ^ Guggenheim, E.A. (1949/1967), Section 1.12, pages 12–13.
- ^ Planck, M. (1923/1926), Section 152A, pages 121–123.
- ^ Prigogine, I. Defay, R. (1950/1954). Chemical Thermodynamics, Longmans, Green & Co., London, page 1.
- ^ Adkins, C.J. (1968/1975). Equilibrium Thermodynamics, second edition, McGraw-Hill, London, ISBN 0-07-084057-1, Section 3.6, pages 43–46.
- ^ Planck, M. (1897/1903), Section 70, pages 48–50.
- ^ Guggenheim, E.A. (1949/1967), Section 3.11, pages 92–92.
- ^ Sommerfeld, A. (1952/1956), Section 1.5 C, pages 23–25.
- ^ Callen, H.B. (1960/1985), Section 6.3.
- ^ Adkins, C.J. (1968/1975). Equilibrium Thermodynamics, second edition, McGraw-Hill, London, ISBN 0-07-084057-1, Section 9.2.
- ^ Planck, M. (1897/1903), Section 236, pages 211–212.
- ^ Serrin, J. (1986). Chapter 1, 'An Outline of Thermodynamical Structure', pages 3–32, especially page 8, in New Perspectives in Thermodynamics, edited by J. Serrin, Springer, Berlin, ISBN 3-540-15931-2.
- ^ Kondepudi, D. (2008). Introduction to Modern Thermodynamics, Wiley, Chichester, ISBN 978-0-470-01598-8, Section 3.2, pages 106–108.
- ^ Truesdell, C.A. (1980). The Tragicomical History of Thermodynamics, 1822–1854, Springer, New York, ISBN 0-387-90403-4, Section 11B, pages 306–310.
- ^ Truesdell, C.A. (1980). The Tragicomical History of Thermodynamics, 1822–1854, Springer, New York, ISBN 0-387-90403-4, Sections 8G,8H, 9A, pages 207–224.
- ^ Kondepudi, D. (2008). Introduction to Modern Thermodynamics, Wiley, Chichester, ISBN 978-0-470-01598-8, Section 3.3, pages 108–114.
- ^ Truesdell, C.A. (1980). The Tragicomical History of Thermodynamics, 1822–1854, Springer, New York, ISBN 0-387-90403-4.
- ^ Kondepudi, D. (2008). Introduction to Modern Thermodynamics, Wiley, Chichester, ISBN 978-0-470-01598-8, Sections 3.1,3.2, pages 97–108.
- ^ Ilya Prigogine, I. & Defay, R., translated by D.H. Everett (1954). Chemical Thermodynamics. Longmans, Green & Co., London, Chapters 18–19.
- ^ Ziegler, H. (1977). An Introduction to Thermomechanics, North-Holland, Amsterdam, ISBN 07204-0432-0.
- ^ Planck M. (1922/1927).
- ^ Guggenheim, E.A. (1949/1967).
- ^ de Groot, S.R., Mazur, P. (1962). Non-equilibrium Thermodynamics, North Holland, Amsterdam.
- ^ Gyarmati, I. (1970). Non-equilibrium Thermodynamics, translated into English by E. Gyarmati and W.F. Heinz, Springer, New York.
- ^ Tro, N.J. (2008). Chemistry. A Molecular Approach, Pearson Prentice-Hall, Upper Saddle River NJ, ISBN 0-13-100065-9.
- ^ C. Carathéodory (1909). "Untersuchungen über die Grundlagen der Thermodynamik". Mathematische Annalen 67: 355–386. A partly reliable translation is to be found at Kestin, J. (1976). The Second Law of Thermodynamics, Dowden, Hutchinson & Ross, Stroudsburg PA..
- ^ a b Turner, L.A. (1962). Simplification of Carathéodory's treatment of thermodynamics, Am. J. Phys. 30: 781–786.
- ^ Turner, L.A. (1962). Further remarks on the zeroth law, Am. J. Phys. 30: 804–806.
- ^ Thomsen, J.S., Hartka, T.J., (1962). Strange Carnot cycles; thermodynamics of a system with a density maximum, Am. J. Phys. 30: 26–33, 30: 388–389.
- ^ C. Carathéodory (1909). "Untersuchungen über die Grundlagen der Thermodynamik". Mathematische Annalen 67: 363. "Axiom II: In jeder beliebigen Umgebung eines willkürlich vorgeschriebenen Anfangszustandes gibt es Zustände, die durch adiabatische Zustandsänderungen nicht beliebig approximiert werden können."
- ^ Duhem, P. (1911). Traité d'Energetique, Gautier-Villars, Paris.
- ^ a b Callen, H.B. (1960/1985).
- ^ a b Truesdell, C., Bharatha, S. (1977). The Concepts and Logic of Classical Thermodynamics as a Theory of Heat Engines, Rigorously Constructed upon the Foundation Laid by S. Carnot and F. Reech, Springer, New York, ISBN 0-387-07971-8.
- ^ Wright, P.G. (1980). Conceptually distinct types of thermodynamics, Eur. J. Phys. 1: 81–84.
- ^ Callen, H.B. (1960/1985), page 14.
- ^ Callen, H.B. (1960/1985), page 16.
- ^ Heisenberg, W. (1958). Physics and Philosophy, Harper & Row, New York, pages 98–99.
- ^ Gislason, E.A., Craig, N.C. (2005). Cementing the foundations of thermodynamics:comparison of system-based and surroundings-based definitions of work and heat, J. Chem. Thermodynamics 37: 954–966.
- ^ Kondepudi, D. (2008). Introduction to Modern Thermodynamics, Wiley, Chichester, ISBN 978-0-470-01598-8, page 63.
- ^ Planck, M. (1922/1927).
- ^ Grandy, W.T., Jr (2008). Entropy and the Time Evolution of Macroscopic Systems, Oxford University Press, Oxford UK, ISBN 9780199546176. Page 49.
- ^ Iribarne, J.V., Godson, W.L. (1973/1989). Atmospheric thermodynamics, second edition, reprinted 1989, Kluwer Academic Publishers, Dordrecht, ISBN90-277-1296-2.
- ^ Peixoto, J.P., Oort, A.H. (1992). Physics of climate, American Institute of Physics, New York, ISBN 0-88318-712-4
- ^ North, G.R., Erukhimova, T.L. (2009). Atmospheric Thermodynamics. Elementary Physics and Chemistry, Cambridge University Press, Cambridge UK, ISBN 978-0-521-89963-5.
- ^ Holton, J.R. (2004). An Introduction of Dynamic Meteorology, fourth edition, Elsevier, Amsterdam, ISBN 978-0-12-354015-7.
- ^ Mak, M. (2011). Atmospheric Dynamics, Cambridge University Press, Cambridge UK, ISBN 978-0-521-19573-7.
Further reading
- Goldstein, Martin, and Inge F. (1993). The Refrigerator and the Universe. Harvard University Press. ISBN 0-674-75325-9. OCLC 32826343. A nontechnical introduction, good on historical and interpretive matters.
- Kazakov, Andrei (July–August 2008). "Web Thermo Tables – an On-Line Version of the TRC Thermodynamic Tables". Journal of Research of the National Institutes of Standards and Technology 113 (4): 209–220. http://nvl-i.nist.gov/pub/nistpubs/jres/113/4/V113.N04.A03.pdf.
The following titles are more technical:
- Cengel, Yunus A., & Boles, Michael A. (2002). Thermodynamics – an Engineering Approach. McGraw Hill. ISBN 0-07-238332-1. OCLC 52263994 57548906 45791449 52263994 57548906.
- Kroemer, Herbert & Kittel, Charles (1980). Thermal Physics. W. H. Freeman Company. ISBN 0-7167-1088-9. OCLC 48236639 5171399 32932988 48236639 5171399.
External links
- Thermodynamics Data & Property Calculation Websites
- Thermodynamics OpenCourseWare from the University of Notre Dame
- Thermodynamics Educational Websites
- Thermodynamics at ScienceWorld
- Biochemistry Thermodynamics
- Thermodynamics and Statistical Mechanics
- Engineering Thermodynamics – A Graphical Approach
- Thermodynamics and Statistical Mechanics by Richard Fitzpatrick
- SklogWiki a wiki dedicated to thermodynamics.
Branches of physics Acoustics • Agrophysics (Soil physics) • Astrophysics • Atmospheric physics • Atomic, molecular, and optical physics • Biophysics (Medical physics · Neurophysics) • Chemical physics • Condensed matter physics • Econophysics • Electromagnetism • Geophysics • Mechanics (Classical mechanics · Continuum mechanics · Quantum mechanics · Fluid mechanics · Thermodynamics · Biomechanics) • Nuclear physics • Optics • Particle physics • Quantum field theory • Relativity (Special relativity · General relativity)Categories:- Thermodynamics
- Chemical engineering
- Fundamental physics concepts
- Greek loanwords
Wikimedia Foundation. 2010.