Clausius theorem

Thermodynamics
Branches Classical · Statistical · Chemical Equilibrium / Non-equilibrium Thermofluids
Laws Zeroth · First · Second · Third
Systems State: Equation of state Ideal gas · Real gas Phase of matter · Equilibrium Control volume · Instruments Processes: Isobaric · Isochoric · Isothermal Adiabatic · Isentropic · Isenthalpic Quasistatic · Polytropic Free expansion Reversibility · Irreversibility Endoreversibility Cycles: Heat engines · Heat pumps Thermal efficiency
System properties Property diagrams Intensive and extensive properties State functions: Temperature / Entropy (intro.) † Pressure / Volume † Chemical potential / Particle no. † († Conjugate variables) Vapor quality Reduced properties Process functions: Work · Heat
Material properties Specific heat capacity  c = T $\partial S$ N $\partial T$ Compressibility  β = − 1 $\partial V$ V $\partial p$ Thermal expansion  α = 1 $\partial V$ V $\partial T$ Property database
Equations Carnot's theorem Clausius theorem Fundamental relation Ideal gas law Maxwell relations Table of thermodynamic equations
Potentials Free energy · Free entropy Internal energy U(S,V) Enthalpy H(S,p) = U + pV Helmholtz free energy A(T,V) = U − TS Gibbs free energy G(T,p) = H − TS
History and culture Philosophy: Entropy and time · Entropy and life Brownian ratchet Maxwell's demon Heat death paradox Loschmidt's paradox Synergetics History: General · Heat · Entropy · Gas laws Perpetual motion Theories: Caloric theory · Vis viva Theory of heat Mechanical equivalent of heat Motive power Publications: "An Experimental Enquiry Concerning ... Heat" "On the Equilibrium of Heterogeneous Substances" "Reflections on the Motive Power of Fire" Timelines of: Thermodynamics · Heat engines Art: Maxwell's thermodynamic surface Education: Entropy as energy dispersal
Scientists Daniel Bernoulli Sadi Carnot Benoît Paul Émile Clapeyron Rudolf Clausius Hermann von Helmholtz Constantin Carathéodory Pierre Duhem Josiah Willard Gibbs James Prescott Joule James Clerk Maxwell Julius Robert von Mayer William Rankine John Smeaton Georg Ernst Stahl Benjamin Thompson William Thomson, 1st Baron Kelvin John James Waterston
v · d · e

The Clausius theorem (1855) states that in a cyclic process

$\oint \frac{\delta Q}{T} \leq 0.$

The equality holds in the reversible case^[1] and the '<' is in the irreversible case. The reversible case is used to introduce the state function entropy. This is because in cyclic process the variation of a state function is zero.

Proof

Proving Clausius Inequality

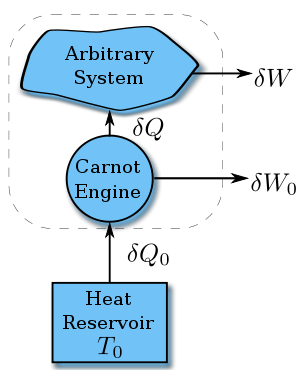
Suppose a system absorbs heat δQ at temperature T. Since the value of $\frac{\delta Q}{T}$ does not depend on the details of how the heat is transferred, we can assume it is from a Carnot engine, which in turn absorbs heat δQ₀ from a heat reservoir with constant temperature T₀.

According to the nature of Carnot cycle,

$\frac{\delta Q}{T}=\frac{\delta Q_0}{T_0}$

$\Rightarrow\delta Q_0=T_0\frac{\delta Q}{T}$

Therefore in one cycle, the total heat absorbed from the reservoir is

$Q_0=T_0\oint\frac{\delta Q}{T}$

Since after a cycle, the system and the Carnot engine as a whole return to its initial status, the difference of the internal energy is zero. Thus according to First Law of Thermodynamics,

Q₀ = ΔU + W + W₀ = W + W₀ = W_total

According to the Kelvin statement of Second Law of thermodynamics, we cannot drain heat from one reservoir and convert them entirely into work without making any other changes, so

$W_\text{total}\leq 0$

Combine all the above and we get Clausius inequality

$\oint\frac{\delta Q}{T}\leq 0$

If the system is reversible, then reverse its path and do the experiment again we can get

$-\oint\frac{\delta Q}{T}\leq 0$

Thus

$\oint\frac{\delta Q}{T}=0$

See also

• Introduction to entropy

References

1. ^ Clausius theorem at Wolfram Research

External links

• Judith McGovern (2004-03-17). "Proof of Clausius's theorem". http://theory.ph.man.ac.uk/~judith/stat_therm/node30.html. Retrieved Octorber 4,2010. 
• "The Clausius Inequality And The Mathematical Statement Of The Second Law". http://ronispc.chem.mcgill.ca/ronis/chem213/hnd10.pdf. Retrieved October 5, 2010.