- Thermodynamic cycle
-
A thermodynamic cycle consists of a series of thermodynamic processes transferring heat and work, while varying pressure, temperature, and other state variables, eventually returning a system to its initial state.[1] In the process of going through this cycle, the system may perform work on its surroundings, thereby acting as a heat engine.
State quantities depend only on the thermodynamic state, and cumulative variation of such properties adds up to zero during a cycle. Process quantities (or path quantities), such as heat and work are process dependent, and cumulative heat and work are non-zero. The first law of thermodynamics dictates that the net heat input is equal to the net work output over any cycle. The repeating nature of the process path allows for continuous operation, making the cycle an important concept in thermodynamics. Thermodynamic cycles often use quasistatic processes to model the workings of actual devices.
Contents
Heat and work
Two primary classes of thermodynamic cycles are power cycles and heat pump cycles. Power cycles are cycles which convert some heat input into a mechanical work output, while heat pump cycles transfer heat from low to high temperatures using mechanical work input. Cycles composed entirely of quasistatic processes can operate as power or heat pump cycles by controlling the process direction. On a pressure volume diagram or temperature entropy diagram, the clockwise and counterclockwise directions indicate power and heat pump cycles, respectively.
Relationship to work
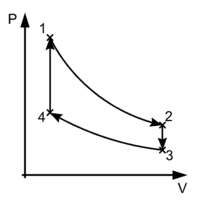
Because the net variation in state properties during a thermodynamic cycle is zero, it forms a closed loop on a PV diagram. A PV diagram's Y axis shows pressure (P) and X axis shows volume (V). The area enclosed by the loop is the work (W) done by the process:
This work is equal to the balance of heat (Q) transferred into the system:
Equation (2) makes a cyclic process similar to an isothermal process: even though the internal energy changes during the course of the cyclic process, when the cyclic process finishes the system's energy is the same as the energy it had when the process began.
If the cyclic process moves clockwise around the loop, then W will be positive, and it represents a heat engine. If it moves counterclockwise, then W will be negative, and it represents a heat pump.
Power cycles
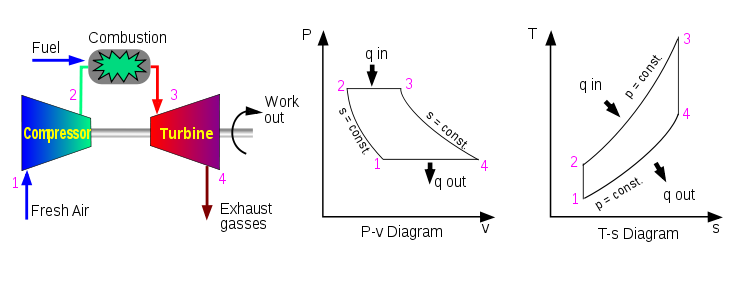
Main article: Heat engineThermodynamic power cycles are the basis for the operation of heat engines, which supply most of the world's electric power and run the vast majority of motor vehicles. Power cycles can be divided according to the type of heat engine they seek to model. The most common cycles that model internal combustion engines are the Otto cycle, which models gasoline engines and the Diesel cycle, which models diesel engines. Cycles that model external combustion engines include the Brayton cycle, which models gas turbines, and the Rankine cycle, which models steam turbines.
For example the pressure-volume mechanical work done in the heat engine cycle, consisting of 4 thermodynamic processes, is:
If no volume change happens in process 4->1 and 2->3, equation (3) simplifies to:
Heat pump cycles
Main article: Heat pump and refrigeration cycleThermodynamic heat pump cycles are the models for heat pumps and refrigerators. The difference between the two is that heat pumps are intended to keep a place warm while refrigerators are designed to cool it. The most common refrigeration cycle is the vapor compression cycle, which models systems using refrigerants that change phase. The absorption refrigeration cycle is an alternative that absorbs the refrigerant in a liquid solution rather than evaporating it. Gas refrigeration cycles include the reversed Brayton cycle and the Hampson-Linde cycle. Regeneration in gas refrigeration allows for the liquefaction of gases.
Modelling real systems
Thermodynamic cycles may be used to model real devices and systems, typically by making a series of assumptions.[2] simplifying assumptions are often necessary to reduce the problem to a more manageable form.[2] For example, as shown in the figure, devices such a gas turbine or jet engine can be modelled as a Brayton cycle. The actual device is made up of a series of stages, each of which is itself modelled as an idealized thermodynamic process. Although each stage which acts on the working fluid is a complex real device, they may be modelled as idealized processes which approximate their real behavior. A further assumption is that the exhaust gases would be passed back through the inlet with a corresponding loss of heat, thus completing the idealized cycle.
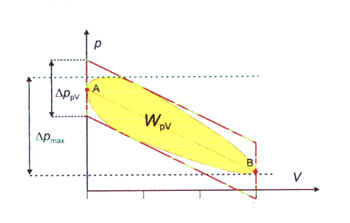
The difference between an idealized cycle and actual performance may be significant.[2] For example, the following images illustrate the differences in work output predicted by an ideal Stirling cycle and the actual performance of a Stirling engine:
Ideal Stirling cycle Actual performance Actual and ideal overlaid, showing difference in work output As work output is represented by the interior of the cycle, there is a significant difference between the predicted work output of the ideal cycle and the actual work output shown by a real engine. It may also be observed that the real individual processes diverge from their idealized counterparts; e.g., isochoric expansion (process 1-2) occurs with some actual volume change.
Well-known thermodynamic cycles
In practice, simple idealized thermodynamic cycles are usually made out of four thermodynamic processes. Any thermodynamic processes may be used. However, when idealized cycles are modeled, often processes where one state variable is kept constant are used, such as an isothermal process (constant temperature), isobaric process (constant pressure), isochoric process (constant volume), isentropic process (constant entropy), or an isenthalpic process (constant enthalpy). Often adiabatic processes are also used, where no heat is exchanged.
Some example thermodynamic cycles and their constituent processes are as follows:
Cycle Process 1-2
(Compression)Process 2-3
(Heat Addition)Process 3-4
(Expansion)Process 4-1
(Heat Rejection)Notes Power cycles normally with external combustion - or heat pump cycles: Bell Coleman adiabatic isobaric adiabatic isobaric A reversed Brayton cycle Brayton adiabatic isobaric adiabatic isobaric Jet engines
aka first Ericsson cycle from 1833Carnot isentropic isothermal isentropic isothermal Ericsson isothermal isobaric isothermal isobaric the second Ericsson cycle from 1853 Scuderi adiabatic variable pressure
and volumeadiabatic isochoric Stirling isothermal isochoric isothermal isochoric Stoddard adiabatic isobaric adiabatic isobaric
Power cycles normally with internal combustion:Diesel adiabatic isobaric adiabatic isochoric Lenoir isobaric isochoric adiabatic isobaric Pulse jets
(Note: 3 of the 4 processes are different)Otto adiabatic isochoric adiabatic isochoric Gasoline / petrol engines Rankine adiabatic isobaric adiabatic isobaric Steam engine Ideal cycle
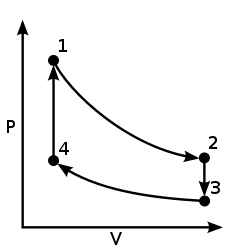
An illustration of an ideal cycle heat engine (arrows clockwise).
An ideal cycle is constructed out of:
- TOP and BOTTOM of the loop: a pair of parallel isobaric processes
- LEFT and RIGHT of the loop: a pair of parallel isochoric processes
Carnot cycle
Main article: Carnot cycleThe Carnot cycle is a cycle composed of the totally reversible processes of isentropic compression and expansion and isothermal heat addition and rejection. The thermal efficiency of a Carnot cycle depends only on the absolute temperatures of the two reservoirs in which heat transfer takes place, and for a power cycle is:
where TL is the lowest cycle temperature and TH the highest. For Carnot power cycles the coefficient of performance for a heat pump is:
and for a refrigerator the coefficient of performance is:
The second law of thermodynamics limits the efficiency and COP for all cyclic devices to levels at or below the Carnot efficiency. The Stirling cycle and Ericsson cycle are two other reversible cycles that use regeneration to obtain isothermal heat transfer.
Stirling cycle
Main article: Stirling cycleA Stirling cycle is like an Otto cycle, except that the adiabats are replaced by isotherms. It is also the same as an Ericsson cycle with the isobaric processes substituted for constant volume processes.
- TOP and BOTTOM of the loop: a pair of quasi-parallel isothermal processes
- LEFT and RIGHT sides of the loop: a pair of parallel isochoric processes
Heat flows into the loop through the top isotherm and the left isochore, and some of this heat flows back out through the bottom isotherm and the right isochore, but most of the heat flow is through the pair of isotherms. This makes sense since all the work done by the cycle is done by the pair of isothermal processes, which are described by Q=W. This suggests that all the net heat comes in through the top isotherm. In fact, all of the heat which comes in through the left isochore comes out through the right isochore: since the top isotherm is all at the same warmer temperature TH and the bottom isotherm is all at the same cooler temperature TC, and since change in energy for an isochore is proportional to change in temperature, then all of the heat coming in through the left isochore is cancelled out exactly by the heat going out the right isochore.
State functions and entropy
If Z is a state function then the balance of Z remains unchanged during a cyclic process:
 .
.
Entropy is a state function and is defined as
so that
 ,
,
then it is clear that for any cyclic process,
meaning that the net entropy change over a cycle is 0.
See also
Thermodynamic cycles External combustion cycles Bell Coleman · Brayton/Joule (externally heated) · Carnot · Ericsson · Ported constant volume[1] · Stirling · Stirling (Pseudo / Adiabatic) · StoddardWith phase changeInternal combustion cycles Mixed cycles Refrigeration cycles Hampson-Linde · Kleemenko · Linde dual-pressure · Pulse tube · Regenerative cooling · Transcritical · Vapor absorption · Vapor-compression · Siemens · VuilleumierUncategorized References
Further reading
- Halliday, Resnick & Walker. Fundamentals of Physics, 5th edition. John Wiley & Sons, 1997. Chapter 21, Entropy and the Second Law of Thermodynamics.
External links
Categories:- Thermodynamic cycles
- Thermodynamics
Wikimedia Foundation. 2010.