Spherical Earth

Medieval artistic representation of a spherical Earth - with compartments representing earth, air, and water (c. 1400).

The concept of a spherical Earth dates back to ancient Greek philosophy from around the 6th century BC,^[1] but remained a matter of philosophical speculation until the 3rd century BC when Hellenistic astronomy established the spherical shape of the earth as a physical given. The Hellenistic paradigm was gradually adopted throughout the Old World during Late Antiquity and the Middle Ages.^[2][3][4][5] A practical demonstration of Earth's sphericity was achieved by Ferdinand Magellan and Juan Sebastian Elcano's expedition's circumnavigation (1519−1521).^[6]

The concept of a spherical Earth displaced earlier beliefs in a flat Earth: In early Mesopotamian mythology, the world was portrayed as a flat disk floating in the ocean and surrounded by a spherical sky,^[7] and this forms the premise for early world maps like those of Anaximander and Hecataeus of Miletus. Other speculations on the shape of Earth include a seven-layered ziggurat or cosmic mountain, alluded to in the Avesta and ancient Persian writings (see seven climes), or a wheel, bowl, or four-cornered plane alluded to in the Rigveda.^[8]

The realization that the figure of the Earth is more accurately described as an ellipsoid dates to the 18th century (Maupertius). In the early 19th century, the flattening of the earth ellipsoid was determined to be of the order of 1/300 (Delambre, Everest). The modern value as determined by the US DoD World Geodetic System since the 1960s is close to 1/298.25.^[9]

History

Antiquity

Classical Greece

Though the earliest evidence of a spherical Earth comes from ancient Greek sources, there is no account of how the sphericity of the Earth was discovered.^[10] A plausible explanation is that it was "the experience of travellers that suggested such an explanation for the variation in the observable altitude and the change in the area of circumpolar stars, a change that was quite drastic between Greek settlements" around the eastern Mediterranean Sea, particularly those between the Nile Delta and the Crimea.^[11]

According to Diogenes Laertius, "[ Pythagoras ] was the first [Greek] who called the earth round; though Theophrastus attributes this to Parmenides, and Zeno to Hesiod."

Pythagoras

Early Greek philosophers alluded to a spherical Earth, though with some ambiguity.^[12] Pythagoras (6th century BC) was among those said to have originated the idea, but this may reflect the ancient Greek practice of ascribing every discovery to one or another of their ancient wise men.^[10] Some idea of the sphericity of the Earth seems to have been known to both Parmenides and Empedocles in the 5th century BC,^[13] and although the idea cannot reliably be ascribed to Pythagoras,^[14] it may, nevertheless have been formulated in the Pythagorean school in the 5th century BC.^[10][13] After the 5th century BC, no Greek writer of repute thought the world was anything but round.^[12]

Herodotus

In The Histories, written 431–425 BC, Herodotus dismisses a report of the sun observed shining from the north. This arises when discussing the circumnavigation of Africa undertaken by Phoenicians under Necho II c. 610–595 BC. (The Histories, 4.43) His dismissive comment attests to a widespread ignorance of the ecliptic's inverted declination in a southern hemisphere.

Plato

Plato (427–347 BC) travelled to southern Italy to study Pythagorean mathematics. When he returned to Athens and established his school, Plato also taught his students that Earth was a sphere though he offered no justifications. If man could soar high above the clouds, Earth would resemble "one of those balls which have leather coverings in twelve pieces, and is decked with various colours, of which the colours used by painters on earth are in a manner samples." ^[15] In Timaeus, his one work that was available throughout the Middle Ages in Latin, we read that the Creator "made the world in the form of a globe, round as from a lathe, having its extremes in every direction equidistant from the centre, the most perfect and the most like itself of all figures",^[16] though the word "world" normally refers to the universe.

Aristotle

Round Earth umbra during the August 2008 lunar eclipse

Aristotle (384–322 BC) was Plato's prize student and "the mind of the school." Aristotle observed "there are stars seen in Egypt and [...] Cyprus which are not seen in the northerly regions." Since this could only happen on a curved surface, he too believed Earth was a sphere "of no great size, for otherwise the effect of so slight a change of place would not be quickly apparent." (De caelo, 298a2–10)

Aristotle provided physical and observational arguments supporting the idea of a spherical Earth:

• Every portion of the Earth tends toward the center until by compression and convergence they form a sphere. (De caelo, 297a9–21)
• Travelers going south see southern constellations rise higher above the horizon; and
• The shadow of Earth on the Moon during a lunar eclipse is round. (De caelo, 297b31–298a10)

The concepts of symmetry, equilibrium and cyclic repetition permeated Aristotle's work. In his Meteorology he divided the world into five climatic zones: two temperate areas separated by a torrid zone near the equator, and two cold inhospitable regions, "one near our upper or northern pole and the other near the ... southern pole," both impenetrable and girdled with ice (Meteorologica, 362a31–35). Although no humans could survive in the frigid zones, inhabitants in the southern temperate regions could exist.

Hellenistic era

Eratosthenes

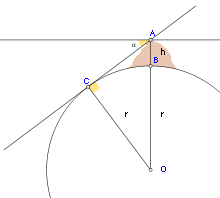
Eratosthenes (276–194 BC) estimated Earth's circumference around 240 BC. He had heard that in Syene the Sun was directly overhead at the summer solstice whereas in Alexandria it still cast a shadow. Using the differing angles the shadows made as the basis of his trigonometric calculations he estimated a circumference of around 250,000 stades. The length of a 'stade' is not precisely known, but Eratosthenes' figure only has an error of around five to fifteen percent.^[17][18][19] Eratosthenes used rough estimates and round numbers, but depending on the length of the stadion, his result is within a margin of between 2% and 20% of the actual meridional circumference, 40,008 kilometres (24,860 mi). Note that Eratosthenes could only measure the circumference of the Earth by assuming that the distance to the Sun is so great that the rays of sunlight are essentially parallel.

Seleucus of Seleucia

Seleucus of Seleucia (c. 190 BC), who lived in the Seleucia region of Mesopotamia, stated that the Earth is spherical (and actually orbits the Sun, influenced by the heliocentric theory of Aristarchus of Samos).

Posidonius

Posidonius (c. 135 – 51 BC) put faith in Eratosthenes's method, though by observing the star Canopus, rather than the sun in establishing the Earth's circumference. In Ptolemy's Geographia, his result was favoured over that of Erastosthenes. Posidonius furthermore expressed the distance of the sun in earth radii.

Roman Empire

From its Greek origins, the idea of a spherical earth, along with much of Greek astronomical thought, slowly spread across the globe and ultimately became the adopted view in all major astronomical traditions:^[2][3][4][5]

In the west, the idea came naturally to the Romans through the lengthy process of cross-fertilization with Hellenistic civilization. Many Roman authors such as Cicero and Pliny refer in their works to the rotundity of the earth as a matter of course.^[20]

Strabo

When a ship is at the horizon, its lower part is invisible due to Earth's curvature. This was one of the first arguments favoring a round-Earth model.

It has been suggested that seafarers probably provided the first observational evidence that the Earth was not flat, based on observations of the horizon. This argument was put forward by the geographer Strabo (c. 64 BC – 24 AD), who suggested that the spherical shape of the Earth was probably known to seafarers around the Mediterranean Sea since at least the time of Homer,^[21] citing a line from the Odyssey^[22] as indicating that the poet Homer was already aware of this as early as the 7th or 8th century BC. Strabo cited various phenomena observed at sea as suggesting that the Earth was spherical. He observed that elevated lights or areas of land were visible to sailors at greater distances than those less elevated, and stated that the curvature of the sea was obviously responsible for this.^[23]

Claudius Ptolemy

Claudius Ptolemy (90–168 AD) lived in Alexandria, the centre of scholarship in the 2nd century. In the Almagest, which remained the standard work of astronomy for 1,400 years, he advanced many arguments for the sphericity of the Earth. Among them was the observation that when sailing towards mountains, they seem to rise from the sea, indicating that they were hidden by the curved surface of the sea. He also gives separate arguments that the Earth is curved north-south and that it is curved east-west.^[24]

He also produced an eight-volume Geographia dealing with the earth. The first part of the Geographia is a discussion of the data and of the methods he used. As with the model of the solar system in the Almagest, Ptolemy put all this information into a grand scheme. He assigned coordinates to all the places and geographic features he knew, in a grid that spanned the globe (although most of this has been lost). Latitude was measured from the equator, as it is today, but Ptolemy preferred to express it as the length of the longest day rather than degrees of arc (the length of the midsummer day increases from 12h to 24h as you go from the equator to the polar circle). He put the meridian of 0 longitude at the most western land he knew, the Canary Islands.

Geographia indicated the countries of "Serica" and "Sinae" (China) at the extreme right, beyond the island of "Taprobane" (Sri Lanka, oversized) and the "Aurea Chersonesus" (Southeast Asian peninsula).

Ptolemy also devised and provided instructions on how to create maps both of the whole inhabited world (oikoumenè) and of the Roman provinces. In the second part of the Geographia he provided the necessary topographic lists, and captions for the maps. His oikoumenè spanned 180 degrees of longitude from the Canary Islands in the Atlantic Ocean to China, and about 81 degrees of latitude from the Arctic to the East Indies and deep into Africa. Ptolemy was well aware that he knew about only a quarter of the globe.

Late Antiquity

Knowledge of the spherical shape of the Earth was received in scholarship of Late Antiquity as a matter of course, in both Neoplatonism and Early Christianity. Theological doubt informed by the flat Earth model implied in the Hebrew Bible inspired some early Christian scholars such as Lactantius, John Chrysostom and Athanasius of Alexandria, but this remained an eccentric current and learned Christian authors like Basil of Caesarea, Aurelius Ambrosius and Augustine of Hippo were clearly aware of the sphericity of the Earth. "Flat Earthism" lingered longest in Syriac Christianity, which tradition laid greater importance on a literalist interpretation of the Old Testament, and authors from that tradition such as Cosmas Indicopleustes presented the Earth as flat as late as in the 6th century. This last remnant of the ancient model of the cosmos disappeared during the 7th century, and from the 8th century and the beginning medieval period, "no cosmographer worthy of note has called into question the sphericity of the Earth."^[25]

Spread to the East

With the rise of Greek culture in the east, Hellenistic astronomy filtered eastwards to ancient India where its profound influence became apparent in the early centuries AD.^[26] The Greek concept of a spherical earth surrounded by the spheres of planets, vehemently supported by astronomers like Varahamihira and Brahmagupta, supplanted the long-standing Indian cosmological belief into a flat and circular earth disk.^[26][27] The works of the classical Indian astronomer and mathematician, Aryabhata (476–550 AD), deal with the sphericity of the Earth and the motion of the planets. The final two parts of his Sanskrit magnum opus, the Aryabhatiya, which were named the Kalakriya ("reckoning of time") and the Gola ("sphere"), state that the Earth is spherical and that its circumference is 4,967 yojanas, which in modern units yields 39,968 km, close to the value already calculated by Eratosthenes in the 3rd century BC.^[28] Aryabhata also stated that the apparent rotation of the celestial objects was due to the actual rotation of the Earth. The Aryabhatiya in turn influenced medieval Islamic scholarship.

Middle Ages

Knowledge of the sphericity of the Earth survived into the medieval corpus of knowledge by direct transmission of the texts of Greek antiquity (Aristotle), and via authors such as Isidore of Seville and Beda Venerabilis. It became increasingly traceable with the rise of scholasticism and medieval learning.^[20] Spread of this knowledge beyond the immediate sphere of Greco-Roman scholarship was necessarily gradual, associated with the pace of Christianisation of Europe. For example, the first evidence of knowledge of the spherical shape of the Earth in Scandinavia is a 12th-century Old Icelandic translation of Elucidarius.^[29]

A non-exhaustive list of more than a hundred Latin and vernacular writers from Late Antiquity and the Middle Ages who were aware that the earth was spherical, has been compiled by Reinhard Krüger, professor for Romance literature at the University of Stuttgart.^[20]

Krüger's list of the 79 authors known by name can be studied by clicking on "show":

Late Antiquity Ampelius, Chalcidius, Macrobius, Martianus Capella, Basil of Caesarea, Ambrose of Milan, Aurelius Augustinus, Paulus Orosius, Jordanes, Cassiodorus, Boethius, Visigoth king Sisebut. Early Middle Ages Isidore of Seville, Beda Venerabilis, Theodulf of Orléans, Vergilius of Salzburg, Irish monk Dicuil, Rabanus Maurus, King Alfred of England, Remigius of Auxerre, Johannes Scotus Eriugena, Leo of Naples (German), Gerbert d’Aurillac (Pope Sylvester II). High Middle Ages Notker the German of Sankt-Gallen, Hermann of Reichenau, Hildegard von Bingen, Petrus Abaelardus, Honorius Augustodunensis, Gautier de Metz, Adam of Bremen, Albertus Magnus, Thomas Aquinas, Berthold of Regensburg, Guillaume de Conches, Philippe de Thaon (French), Abu-Idrisi, Bernardus Silvestris, Petrus Comestor, Thierry de Chartres, Gautier de Châtillon, Alexander Neckam, Alain de Lille, Averroes, Snorri Sturluson, Moshe ben Maimon, Lambert de Saint-Omer (German), Gervasius of Tilbury, Robert Grosseteste, Johannes de Sacrobosco, Thomas de Cantimpré, Peire de Corbian, Vincent de Beauvais, Robertus Anglicus, Juan Gil de Zámora (Spanish), Ristoro d'Arezzo, Roger Bacon, Jean de Meung, Brunetto Latini, Alfonso X of Castile. Late Middle Ages Marco Polo, Dante Alighieri, Meister Eckhart, Enea Silvio Piccolomini (Pope Pius II), Perot de Garbelei (German) (divisiones mundi), Cecco d'Ascoli, Fazio degli Uberti (Italian), Levi ben Gershon, Konrad of Megenberg, Nicole Oresme, Petrus Aliacensis, Alfonso de la Torre (German), Toscanelli, Brochard the German (German), Jean de Mandeville, Christine de Pizan, Geoffrey Chaucer, William Caxton, Martin Behaim, Christopher Columbus.

Christian world

Spherical earth with the four seasons. Illustration in 12th century book Liber Divinorum Operum by Hildegard of Bingen

Isidore of Seville

Bishop Isidore of Seville (560–636) taught in his widely read encyclopedia, the Etymologies, that the Earth was round. While some writers have thought he referred to a spherical Earth;^[30] this and other writings make it clear that he considered the Earth to be disk or wheel-shaped.^[31] He didn't admit the possibility of people dwelling at the antipodes, considering them as legendary^[32] and noting that there was no evidence for their existence.^[33]

Bede the Venerable

The monk Bede (c. 672–735) wrote in his influential treatise on computus, The Reckoning of Time, that the Earth was round, explaining the unequal length of daylight from "the roundness of the Earth, for not without reason is it called 'the orb of the world' on the pages of Holy Scripture and of ordinary literature. It is, in fact, set like a sphere in the middle of the whole universe." (De temporum ratione, 32). The large number of surviving manuscripts of The Reckoning of Time, copied to meet the Carolingian requirement that all priests should study the computus, indicates that many, if not most, priests were exposed to the idea of the sphericity of the Earth.^[34] Ælfric of Eynsham paraphrased Bede into Old English, saying "Now the Earth's roundness and the Sun's orbit constitute the obstacle to the day's being equally long in every land."^[35]

Bede was lucid about earth's sphericity, writing "We call the earth a globe, not as if the shape of a sphere were expressed in the diversity of plains and mountains, but because, if all things are included in the outline, the earth's circumference will represent the figure of a perfect globe... For truly it is an orb placed in the center of the universe; in its width it is like a circle, and not circular like a shield but rather like a ball, and it extends from its center with perfect roundness on all sides."^[36]

Anania Shirakatsi

The 7th-century Armenian scholar Anania Shirakatsi described the world as "being like an egg with a spherical yolk (the globe) surrounded by a layer of white (the atmosphere) and covered with a hard shell (the sky)." ^[37]

High Middle Ages

During the High Middle Ages, the astronomical knowledge in Christian Europe is extended beyond what was transmitted directly from ancient authors by transmission of learning from Medieval Islamic astronomy. An early recipient of such learning was Gerbert d'Aurillac, the later Pope Silvester II.

Saint Hildegard (Hildegard von Bingen, 1098–1179), depicts the spherical earth several times in her work Liber Divinorum Operum. [5]

Johannes de Sacrobosco (c. 1195 – c. 1256 AD) wrote a famous work on Astronomy called Tractatus de Sphaera, based on Ptolemy, in which he considers the Earth to be spherical.^[38]

Late Middle Ages

John Gower prepares to shoot the world, a sphere with compartments representing earth, air, and water (Vox Clamantis, around 1400)

Dante's Divine Comedy, written in Italian in the early 14th century, portrays Earth as a sphere, discussing implications such as the different stars visible in the southern hemisphere, the altered position of the sun, and the various timezones of the Earth. Also, the Elucidarium of Honorius Augustodunensis (c. 1120), an important manual for the instruction of lesser clergy, which was translated into Middle English, Old French, Middle High German, Old Russian, Middle Dutch, Old Norse, Icelandic, Spanish, and several Italian dialects, explicitly refers to a spherical Earth. Likewise, the fact that Bertold von Regensburg (mid-13th century) used the spherical Earth as a sermonic illustration shows that he could assume this knowledge among his congregation. The sermon was held in the vernacular German, and thus was not intended for a learned audience.

Portuguese exploration of Africa and Asia, Columbus voyage to the Americas (1492) and finally Ferdinand Magellan's circumnavigation of the earth (1519–21) provided practical proofs for the global shape of the earth, while European colonists planted the idea in the American colonies.

Islamic world

Islamic astronomy inherited the idea of a spherical earth from the Greek astronomical tradition.^[39] The Islamic theoretical framework largely relied on the fundamental contributions of Aristotle (De caelo) and Ptolemy (Almagest), both of which worked with the premise that the earth was spherical and at the center of the universe (geocentric model).^[39]

Early Islamic scholars recognized earth's sphericity,^[40] leading Muslim mathematicians to develop spherical trigonometry^[41] in order to further mensuration and to calculate the distance and direction from any given point on the Earth to Mecca. This determined the Qibla, or Muslim direction of prayer.

Al-Ma'mun

Around 830 AD, Caliph Al-Ma'mun commissioned a group of Muslim astronomers and Muslim geographers to measure the distance from Tadmur (Palmyra) to al-Raqqah, in modern Syria. They found the cities to be separated by one degree of latitude and the meridian arc distance between them to be 66²⁄₃ miles and thus calculated the Earth's circumference to be 24,000 miles.^[42]

Another estimate given by his astronomers was 56²⁄₃ Arabic miles (111.8 km) per degree, which corresponds to a circumference of 40,248 km, very close to the currently modern values of 111.3 km per degree and 40,068 km circumference, respectively.^[43]

Al-Farghānī

Al-Farghānī (Latinized as Alfraganus) was a Persian astronomer of the 9th century involved in measuring the diameter of the Earth, and commissioned by Al-Ma'mun. His estimate given above for a degree (56²⁄₃ Arabic miles) was much more accurate than the 60²⁄₃ Roman miles (89.7 km) given by Ptolemy. Christopher Columbus uncritically used Alfraganus's figure as if it were in Roman miles instead of in Arabic miles, in order to prove a smaller size of the Earth than that propounded by Ptolemy.^[44]

Biruni

Biruni's Method for calculation of Earth's radius

Abu Rayhan Biruni (973-1048) used a new method to accurately compute the Earth's circumference, by which he arrived at a value that was close to modern values for the Earth's circumference.^[45] His estimate of 6,339.9 km for the Earth radius was only 16.8 km less than the modern value of 6,356.7 km. In contrast to his predecessors who measured the Earth's circumference by sighting the Sun simultaneously from two different locations, Biruni developed a new method of using trigonometric calculations based on the angle between a plain and mountain top which yielded more accurate measurements of the Earth's circumference and made it possible for it to be measured by a single person from a single location.^[46][47] Biruni's method was intended to avoid "walking across hot, dusty deserts" and the idea came to him when he was on top of a tall mountain in India. From the top of the mountain, he sighted the angle to the horizon which, along with the mountain's height (which he calculated beforehand), allowed him to calculate the curvature of the Earth.^[48][49] He also made use of algebra to formulate trigonometric equations and used the astrolabe to measure angles.^[50]

John J. O'Connor and Edmund F. Robertson write in the MacTutor History of Mathematics archive:

"Important contributions to geodesy and geography were also made by Biruni. He introduced techniques to measure the earth and distances on it using triangulation. He found the radius of the earth to be 6339.6 km, a value not obtained in the West until the 16th century. His Masudic canon contains a table giving the coordinates of six hundred places, almost all of which he had direct knowledge."^[51]

Early Modern period

Circumnavigation of the globe

Further information: Age of Discovery

The Erdapfel, the oldest surviving terrestrial globe (1492/93)

The first direct demonstration of Earth's sphericity came in the form of the first circumnavigation in history, an expedition captained by Portuguese explorer Ferdinand Magellan.^[52] The expedition was financed by the Spanish Crown. On August 10, 1519, the five ships under Magellan's command departed from Seville. They crossed the Atlantic Ocean, passed through the Strait of Magellan, crossed the Pacific, and arrived in Cebu, where Magellan was killed by Philippine natives in a battle. His second in command, the Spaniard Juan Sebastián Elcano, continued the expedition and, on September 6, 1522, arrived at Seville, completing the circumnavigation. Charles I of Spain, in recognition of his feat, gave Elcano a coat of arms with the motto Primus circumdedisti me (in Latin, "You went around me first").^[53]

A circumnavigation alone does not prove that the earth is spherical. It could be cylindric or irregularly globular or one of many other shapes. Still, combined with trigonometric evidence of the form used by Eratosthenes 1,700 years prior, the Magellan expedition removed any reasonable doubt in educated circles in Europe.

Ming China

In the 17th century, the idea of a spherical earth, now considerably advanced by Western Astronomy, ultimately spread to Ming China, when Jesuit missionaries, who held high positions as astronomers at the imperial court, successfully challenged the Chinese belief that the earth was flat and square.^[54][55][56]

Summary of evidence for a spherical earth

These are given in an order which approximates how they were observed historically:

1. When at sea it is possible to see high mountains or elevated lights in the distance before lower lying ground and the masts of boats before the hull. It is also possible to see further by climbing higher in the ship, or, when on land, on high cliffs.
2. The sun is lower in the sky as you travel north, but stars such as Polaris, the north star, are higher in the sky. Other bright stars such as Canopus, visible in Egypt, disappear from the sky.
3. The earth throws a circular shadow on the moon during a lunar eclipse.
4. The times reported for lunar eclipses (which are seen simultaneously) are many hours later in the east (e.g. India) than in the west (e.g. Europe). Local times are confirmed later by travel using chronometers and telegraphic communication.
5. When you travel far south, to Ethiopia or India, the sun throws a shadow south at certain times of the year. Even further (e.g. Argentina) and the shadow is always in the south.
6. It is possible to circumnavigate the world; that is, to travel around the world and return to where you started.
7. Travelers who circumnavigate the earth observe the gain or loss of a day relative to those who did not. See also International Date Line.
8. An artificial satellite can circle the earth continuously and even be geostationary.
9. The earth appears as a disc on photographs taken from space, regardless of the vantage point.

Several of these arguments have alternative explanations by themselves. e.g. the shadow thrown by a lunar eclipse could be caused by a disk-shaped earth. Similarly the north-south movement of stars in the sky with travel could mean they are much closer to earth. However, the arguments strengthen each together.

Geodesy

Main article: Geodesy

Geodesy, also called geodetics, is the scientific discipline that deals with the measurement and representation of the Earth, its gravitational field and geodynamic phenomena (polar motion, Earth tides, and crustal motion) in three-dimensional time-varying space.

Geodesy is primarily concerned with positioning and the gravity field and geometrical aspects of their temporal variations, although it can also include the study of Earth's magnetic field. Especially in the German speaking world, geodesy is divided into geomensuration ("Erdmessung" or "höhere Geodäsie"), which is concerned with measuring the Earth on a global scale, and surveying ("Ingenieurgeodäsie"), which is concerned with measuring parts of the surface.

The Earth's shape can be thought of in at least two ways;

• as the shape of the geoid, the mean sea level of the world ocean; or
• as the shape of Earth's land surface as it rises above and falls below the sea.

As the science of geodesy measured Earth more accurately, the shape of the geoid was first found not to be a perfect sphere but to approximate an oblate spheroid, a specific type of ellipsoid. More recent measurements have measured the geoid to unprecedented accuracy, revealing mass concentrations beneath Earth's surface.

See also

• Celestial sphere
• Earth radius
• Figure of the Earth
• Flat Earth
• Geographical distance
• Myth of the Flat Earth
• Physical geodesy
• Terra Australis
• WGS 84

References

1. ^ Dicks, D.R. (1970). Early Greek Astronomy to Aristotle. Ithaca, N.Y.: Cornell University Press. pp. 72–198. ISBN 9780801405617. 
2. ^ ^{a b} Continuation into Roman and medieval thought: Reinhard Krüger: "Materialien und Dokumente zur mittelalterlichen Erdkugeltheorie von der Spätantike bis zur Kolumbusfahrt (1492)"
3. ^ ^{a b} Direct adoption of the Greek concept by Islam: Ragep, F. Jamil: "Astronomy", in: Krämer, Gudrun (ed.) et al.: Encyclopaedia of Islam, THREE, Brill 2010, without page numbers
4. ^ ^{a b} Direct adoption by India: D. Pingree: "History of Mathematical Astronomy in India", Dictionary of Scientific Biography, Vol. 15 (1978), pp. 533−633 (554f.); Glick, Thomas F., Livesey, Steven John, Wallis, Faith (eds.): "Medieval Science, Technology, and Medicine: An Encyclopedia", Routledge, New York 2005, ISBN0-415-96930-1, p. 463
5. ^ ^{a b} Adoption by China via European science: Jean-Claude Martzloff, “Space and Time in Chinese Texts of Astronomy and of Mathematical Astronomy in the Seventeenth and Eighteenth Centuries”, Chinese Science 11 (1993-94): 66–92 (69) and Christopher Cullen, "A Chinese Eratosthenes of the Flat Earth: A Study of a Fragment of Cosmology in Huai Nan tzu 淮 南 子", Bulletin of the School of Oriental and African Studies, Vol. 39, No. 1 (1976), pp. 106–127 (107)
6. ^ Pigafetta, Antonio (1906). Magellan's Voyage around the World. Arthur A. Clark. [1]
7. ^ Otto E. Neugebauer (1975). A History of Ancient Mathematical Astronomy. Birkhäuser. p. 577. ISBN 354006995X 
8. ^ Menon, CPS. Early Astronomy and Cosmology. Whitegishm MT, USA: Kessinger Publishing. p. 68. [2]
9. ^ See figure of the Earth and Earth radius for details. Recent measurements from satellites suggest that the Earth is, in fact, slightly pear-shaped. Hugh Thurston, Early Astronomy, (New York: Springer-Verlag), p. 119. ISBN 0-387-94107-X.
10. ^ ^{a b c} James Evans, (1998), The History and Practice of Ancient Astronomy, page 47, Oxford University Press
11. ^ Otto E. Neugebauer (1975). A History of Ancient Mathematical Astronomy. Birkhäuser. pp. 575–6. ISBN 354006995X 
12. ^ ^{a b} Dicks, D.R. (1970). Early Greek Astronomy to Aristotle. Ithaca, N.Y.: Cornell University Press. pp. 68. ISBN 9780801405617. 
13. ^ ^{a b} Charles H. Kahn, (2001), Pythagoras and the Pythagoreans: a brief history, page 53. Hackett
14. ^ Pythagoras entry by Carl Huffman in the Stanford Encyclopedia of Philosophy
15. ^ Plato. Phaedo. p. 110b. 
16. ^ Plato. Timaeus. p. 33. 
17. ^ Van Helden, Albert (1985). Measuring the Universe: Cosmic Dimensions from Aristarchus to Halley. University of Chicago Press. pp. 4–5. ISBN 0-226-84882-5. 
18. ^ "JSC NES School Measures Up". NASA. 11 April 2006. http://www.nasa.gov/audience/forstudents/5-8/features/F_JSC_NES_School_Measures_Up.html. Retrieved 7 Oct 2010. 
19. ^ "The Round Earth". NASA. 12 December 2004. http://www-istp.gsfc.nasa.gov/stargaze/Scolumb.htm. Retrieved 24 January 2008. 
20. ^ ^{a b c} Reinhard Krüger: "Materialien und Dokumente zur mittelalterlichen Erdkugeltheorie von der Spätantike bis zur Kolumbusfahrt (1492)"
21. ^ Hugh Thurston, Early Astronomy, (New York: Springer-Verlag), p. 118. ISBN 0-387-94107-X.
22. ^ Odyssey, Bk. 5 393: "As he rose on the swell he looked eagerly ahead, and could see land quite near." Samuel Butler's translation is available online.
23. ^ Strabo (1960) [1917]. The Geography of Strabo, in Eight Volumes. Loeb Classical Library edition, translated by Horace Leonard Jones, A.M., Ph.D.. London: William Heinemann. , Vol.I Bk. I para. 20, pp.41, 43. An earlier edition is available online.
24. ^ Ptolemy. Almagest. pp. I.4.  as quoted in Grant, Edward (1974). A Source Book in Medieval Science. Harvard University Press. pp. 63–4. 
25. ^ Klaus Anselm Vogel, "Sphaera terrae - das mittelalterliche Bild der Erde und die kosmographische Revolution," PhD dissertation Georg-August-Universität Göttingen, 1995, p. 19.
26. ^ ^{a b} D. Pingree: "History of Mathematical Astronomy in India", Dictionary of Scientific Biography, Vol. 15 (1978), pp. 533−633 (533, 554f.)
27. ^ Glick, Thomas F., Livesey, Steven John, Wallis, Faith (eds.): "Medieval Science, Technology, and Medicine: An Encyclopedia", Routledge, New York 2005, ISBN0-415-96930-1, p. 463
28. ^ Aryabhata_I biography. http://www.gongol.com/research/math/aryabhatiya The Aryabhatiya: Foundations of Indian Mathematics
29. ^ Rudolf Simek, Altnordische Kosmographie, Berlin, 1990, p. 102.
30. ^ Isidore, Etymologiae, XIV.ii.1 [3]; Wesley M. Stevens, "The Figure of the Earth in Isidore's De natura rerum", Isis, 71(1980): 268-277.
31. ^ Referring to the five circles in De Natura Rerum X 5: "The explanation of the passage and of the figure which illustrates it seems to be that Isidore accepted the terminology of the spherical earth from Hyginus without taking the time to understand it—if indeed he had the ability to do so—and applied it without compunction to the flat earth." Ernest Brehaut (1912). Encyclopedist of the Flat Earth. p. 30.  J. Fontaine refers to this passage as a "scientific absurdity".Isidore of Seville (1960). J. Fontaine. ed. Traité de la Nature. p. 16. 
32. ^ Isidore, Etymologiae, XIV.v.17 [4].
33. ^ Isidore, Etymologiae, IX.ii.133 [5].
34. ^ Faith Wallis, trans., Bede: The Reckoning of Time, (Liverpool: Liverpool Univ. Pr., 2004), pp. lxxxv-lxxxix.
35. ^ Ælfric of Eynsham, On the Seasons of the Year, Peter Baker, trans
36. ^ Russell, Jeffrey B. 1991. Inventing the Flat Earth. New York: Praeger Publishers. p. 87.
37. ^ Hewson, Robert H. "Science in Seventh-Century Armenia: Ananias of Sirak, Isis, Vol. 59, No. 1, (Spring, 1968), pp. 32–45
38. ^ Olaf Pedersen, "In Quest of Sacrobosco", Journal for the History of Astronomy, 16(1985): 175-221
39. ^ ^{a b} Ragep, F. Jamil: "Astronomy", in: Krämer, Gudrun (ed.) et al.: Encyclopaedia of Islam, THREE, Brill 2010, without page numbers
40. ^ Muhammad Hamidullah. L'Islam et son impulsion scientifique originelle, Tiers-Monde, 1982, vol. 23, n° 92, p. 789.
41. ^ David A. King, Astronomy in the Service of Islam, (Aldershot (U.K.): Variorum), 1993.
42. ^ Gharā'ib al-funūn wa-mulah al-`uyūn (The Book of Curiosities of the Sciences and Marvels for the Eyes), 2.1 "On the mensuration of the Earth and its division into seven climes, as related by Ptolemy and others," (ff. 22b-23a)[3]
43. ^ Edward S. Kennedy, Mathematical Geography, pp=187–8, in (Rashed & Morelon 1996, pp. 185–201)
44. ^ Felipe Fernández-Armesto, Columbus and the conquest of the impossible, pp. 20–1, Phoenix Press, 1974.
45. ^ James S. Aber (2003). Alberuni calculated the Earth's circumference at a small town of Pind Dadan Khan, District Jhelum, Punjab, Pakistan.Abu Rayhan al-Biruni, Emporia State University.
46. ^ Lenn Evan Goodman (1992), Avicenna, p. 31, Routledge, ISBN 041501929X.
47. ^ Behnaz Savizi (2007). "Applicable Problems in History of Mathematics: Practical Examples for the Classroom". Teaching Mathematics and Its Applications (Oxford University Press) 26 (1): 45–50. doi:10.1093/teamat/hrl009. http://people.exeter.ac.uk/PErnest/pome19/Savizi%20-%20Applicable%20Problems.doc. Retrieved 2010-02-21. 
48. ^ Mercier, Raymond P. (1992). "Geodesy". In J. B. Harley, David Woodward (eds.). The History of Cartography: Vol. 2.1, Cartography in the traditional Islamic and South Asian societies. Chicago & London: University of Chicago Press. pp. 182–184. ISBN 978-0-226-31635-2. 
49. ^ Beatrice Lumpkin (1997). Geometry Activities from Many Cultures. Walch Publishing. pp. 60 & 112–3. ISBN 0825132851  [4]
50. ^ Jim Al-Khalili, The Empire of Reason 2/6 (Science and Islam - Episode 2 of 3) on YouTube, BBC
51. ^ O'Connor, John J.; Robertson, Edmund F., "Al-Biruni", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Al-Biruni.html .
52. ^ Nowell, Charles E. ed. (1962). Magellan's Voyage around the World: Three Contemporary Accounts. Evanston: NU Press.
53. ^ Joseph Jacobs(2006), "The story of geographical discovery" p.90
54. ^ "Jean-Claude Martzloff, "Space and Time in Chinese Texts of Astronomy and of Mathematical Astronomy in the Seventeenth and Eighteenth Centuries", Chinese Science 11 (1993-94): 66-92 (69)" (PDF). http://www.uni-tuebingen.de/uni/ans/eastm/back/cs11/cs11-4-martzloff.pdf. 
55. ^ Christopher Cullen, “Joseph Needham on Chinese Astronomy”, Past and Present, No. 87. (May, 1980), pp. 39–53 (42 & 49)
56. ^ Christopher Cullen, "A Chinese Eratosthenes of the Flat Earth: A Study of a Fragment of Cosmology in Huai Nan tzu 淮 南 子", Bulletin of the School of Oriental and African Studies, Vol. 39, No. 1 (1976), pp. 106–127 (107-109)

External links

• You say the earth is round? Prove it (from The Straight Dope)
• Oblate Spheroid
• NASA-Most Changes in Earth's Shape Are Due to Changes in Climate
• The Round Earth and Christopher Columbus, educational web site