- Spherical trigonometry
-
Spherical trigonometry is a branch of spherical geometry which deals with polygons (especially triangles) on the sphere and the relationships between the sides and the angles. This is of great importance for calculations in astronomy and earth-surface, orbital and space navigation.
Contents
History
Spherical triangles were studied by early Greek mathematicians such as Menelaus of Alexandria, who wrote a book on spherical triangles called Sphaerica and developed Menelaus' theorem.[1] E. S. Kennedy, however, points out that while it was possible in ancient mathematics to compute the magnitudes of a spherical figure, in principle, by use of the table of chords and Menelaus' theorem, the application of the theorem to spherical problems was very difficult in practice.[2]
Islamic world
Further advances were made in the Islamic world. In order to observe holy days on the Islamic calendar in which timings were determined by phases of the moon, the astronomers initially used Menalaus' method to calculate the place of the moon and stars, though this method proved to be clumsy and difficult. It involved setting up two intersecting right triangles; by applying Menelaus' theorem it was possible to solve one of the six sides, but only if the other five sides were known. To tell the time from the sun's altitude, for instance, repeated applications of Menelaus' theorem were required. For medieval Islamic astronomers, there was an obvious challenge to find a simpler trigonometric method.[3]
In the early 9th century, Muhammad ibn Mūsā al-Khwārizmī, a Persian Mathematician, was an early pioneer in spherical trigonometry and wrote a treatise on the subject.[4] In the 10th century, another Persian Mathematician Abū al-Wafā' al-Būzjānī established the angle addition formulas, e.g., sin(a + b), and discovered the sine formula for spherical trigonometry:[5]
Here, a, b, and c are the angles at the centre of the sphere subtended by the three sides of the triangle, and α, β, and γ are the angles between the sides, where angle α is opposite the side which subtends angle a, etc.
Al-Jayyani (989-1079), an Arabic mathematician in Islamic Iberian Peninsula, wrote what some consider the first treatise on spherical trigonometry, circa 1060, entitled The book of unknown arcs of a sphere,[6] in which spherical trigonometry was brought into its modern form. Al-Jayyani's book "contains formulae for right-angle triangles, the general law of sines and the solution of a spherical triangle by means of the polar triangle". This treatise later had a "strong influence on European mathematics", and his "definition of ratios as numbers" and "method of solving a spherical triangle when all sides are unknown" are likely to have influenced Regiomontanus.[6][unreliable source?]
In the 13th century, Persian mathematician Nasīr al-Dīn al-Tūsī was the first to treat trigonometry as a mathematical discipline independent from astronomy, and he further developed spherical trigonometry, bringing it to its present form.[7] He listed the six distinct cases of a right-angled triangle in spherical trigonometry. In his On the Sector Figure, he also stated the law of sines for plane and spherical triangles, and discovered the law of tangents for spherical triangles.[8]
Lines and angles on a sphere
On the surface of a sphere, the closest analogue to straight lines are great circles, i.e. circles whose centers coincide with the center of the sphere. For example, simplifying the shape of the Earth (the geoid) to a sphere, the meridians and the equator are great circles on its surface, while non-equatorial lines of latitude are small circles. As with a line segment in a plane, an arc of a great circle (subtending less than 180°) on a sphere is the shortest path lying on the sphere between its two endpoints. Great circles are special cases of the concept of a geodesic.
An area on the sphere bounded by arcs of great circles is called a spherical polygon. Note that, unlike the case on a plane, spherical "biangles" (two-sided analogs to triangle) are possible (such as a slice cut out of an orange). Such a polygon is also called a lune.
The sides of these polygons are specified not by their lengths, but by the angles at the sphere's center subtended to the endpoints of the sides. Note that this arc angle, measured in radians, when multiplied by the sphere's radius equals the arc length. (In the special case of polygons on the surface of a sphere of radius one, the arc length of any side equals its subtended angle.)
Hence, a spherical triangle is specified as usual by its corner angles and its sides, but the sides are given not by their length, but by their arc angle.
The sum of the vertex angles of spherical triangles is always larger than the sum of the angles of plane triangles, which is exactly 180°. The amount E by which the sum of the angles exceeds 180° is called spherical excess:
where α, β and γ denote the angles in degrees. Girard's theorem, named after the 16th century French mathematician Albert Girard (earlier discovered but not published by the English mathematician Thomas Harriot), states that this surplus determines the surface area of any spherical triangle:
where R is the radius of the sphere. From this and the area formula for a sphere it follows that the sum of the angles of a spherical triangle is
 .
.The analogous result holds for hyperbolic triangles, with "excess" replaced by "defect"; these are both special cases of the Gauss-Bonnet theorem.
It follows from here that there are no non-trivial similar triangles (triangles with equal angles but different side lengths and area) on a sphere. In the special case of a sphere of radius 1, the area simply equals the excess angle: A = E. One can also use Girard's formula to obtain the discrete Gauss-Bonnet theorem.
To solve a geometric problem on the sphere, one dissects the relevant figure into right spherical triangles (i.e.: one of the triangle's corner angles is 90°) because one can then use Napier's pentagon.
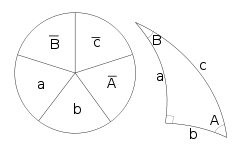
Napier's Pentagon
Napier's pentagon (also known as Napier's circle) is a mnemonic aid that helps to find all relations between the angles in a right spherical triangle.
Write the six angles of the triangle (three vertex angles, three arc angles) in the form of a circle, sticking to the order as they appear in the triangle (i.e.: start with a corner angle, write the arc angle of an attached side next to it, proceed with the next corner angle, etc. and close the circle). Then cross out the 90° corner angle and replace all angles non-adjacent to it by their complement to 90° (i.e. replace, say, B by 90° − B). The five numbers that you now have on your paper form Napier's Pentagon (or Napier's Circle). For any choice of three angles, one (the middle angle) will be either adjacent to or opposite the other two angles. Then Napier's Rules hold that the sine of the middle angle is equal to:
- the product of the tangents of the adjacent angles
- the product of the cosines of the opposite angles
The mnemonic for remembering the trigonometric function to use is that the first vowel of the adjective describing each angle (e.g., i for middle) is the first vowel of the name of the function. As an example, starting with the angle
 , we can obtain the formula:
, we can obtain the formula:Using the identities for complementary angles, this becomes:
- cos(B) = tan(a)cot(c) = cos(b)sin(A).
See also the Haversine formula, which relates the lengths of sides and angles in spherical triangles in a numerically stable form for navigation.
Congruent triangles on a sphere
As with plane triangles, on a sphere two triangles sharing the same sequence of angle, side, angle (ASA) are necessarily congruent (that is, they have three identical sides and three identical angles). This can be seen as follows: One can situate one of the vertices with a given angle at the south pole and run the side with given length up the prime meridian. Knowing both angles at either end of the segment of fixed length ensures that the other two sides emanate with a uniquely determined trajectory, and thus will meet each other at a uniquely determined point; thus ASA is valid.
On the other hand, a like sequence of side, side, side (SSS) does not ensure congruence: For example, with side lengths of π, π / 2, and π / 2 one has a continuous family of non-congruent triangles.
Identities
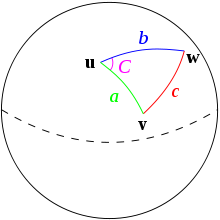
Spherical triangles satisfy a spherical law of cosines
The identity may be derived by considering the triangles formed by the tangent lines to the spherical triangle subtending angle C and using the plane law of cosines. Moreover, it reduces to the plane law in the small area limit.
They also satisfy an analogue of the law of sines
And finally, they satisfy the half-side formula :
where S = (A + B + C) / 2.
See also
References
- ^ O'Connor, John J.; Robertson, Edmund F., "Menelaus of Alexandria", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Menelaus.html.
- ^ Kennedy, E. S. (1969), "The History of Trigonometry", 31st Yearbook (National Council of Teachers of Mathematics, Washington DC): 337 (cf. Haq, Syed Nomanul, The Indian and Persian background, p. 68, in Seyyed Hossein Nasr, Oliver Leaman (1996), History of Islamic Philosophy, Routledge, pp. 52–70, ISBN 0415131596)
- ^ Gingerich, Owen (April 1986), "Islamic astronomy", Scientific American 254 (10): 74, http://faculty.kfupm.edu.sa/PHYS/alshukri/PHYS215/Islamic_astronomy.htm, retrieved 2008-05-18
- ^ O'Connor, John J.; Robertson, Edmund F., "Spherical trigonometry", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Al-Khwarizmi.html.
- ^ Jacques Sesiano, "Islamic mathematics", p. 157, in Selin, Helaine; D'Ambrosio, Ubiratan (2000), Mathematics Across Cultures: The History of Non-western Mathematics, Springer, ISBN 1402002602
- ^ a b O'Connor, John J.; Robertson, Edmund F., "Abu Abd Allah Muhammad ibn Muadh Al-Jayyani", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Al-Jayyani.html.
- ^ "trigonometry". Encyclopædia Britannica. http://www.britannica.com/EBchecked/topic/605281/trigonometry. Retrieved 2008-07-21.
- ^ Berggren, J. Lennart (2007), "Mathematics in Medieval Islam", The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook, Princeton University Press, p. 518, ISBN 9780691114859
- Isaac Todhunter: Spherical Trigonometry: For the Use of Colleges and Schools. Macmillan & Co. 1863 (complete online version (Google Books))
External links
- Wolfram's mathworld: Spherical Trigonometry a more thorough list of identities, with some derivation
- Wolfram's mathworld: Spherical Triangle nice applet
- Intro to Spherical Trig. Includes discussion of The Napier circle and Napier's rules
- Spherical Trigonometry — for the use of colleges and schools by I. Todhunter, M.A., F.R.S. Historical Math Monograph posted by Cornell University Library.
- A Visual Proof of Girard's Theorem by Okay Arik, the Wolfram Demonstrations Project.
Categories:
Wikimedia Foundation. 2010.