Lune (mathematics)

In geometry, a lune is either of two figures, both shaped roughly like a crescent Moon. The word "lune" derives from luna, the Latin word for Moon.

Plane geometry

In plane geometry, a lune is the concave-convex area bounded by two circular arcs, while a convex-convex area is termed a lens. ^[1]

Formally, a lune is the relative complement of one disk in another (where they intersect but neither is a subset of the other). Alternatively, if A and B are disks, then $L = A - A \cap B$ is a lune.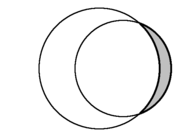

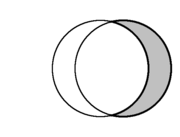
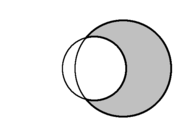
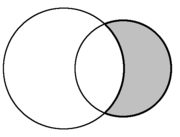
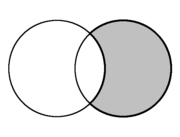
In plane geometry, the crescent shape formed from two intersecting circles is called a lune (in gray). There are two lunes in each diagram only one of which is shaded

Spherical geometry

A spherical lune. The two great circles are shown as thin black lines, whereas the lune itself (shown in green) is outlined in thick black lines, corresponding to its defining half great circles. The great circles bound three other lunes as well, and intersect at two polar opposite points, such as the North and South poles.

In spherical geometry, a lune is an area on a sphere bounded by two half great circles,^[2] which is also called a digon or a diangle or (in German) a Zweieck. Great circles are the largest possible circles on a sphere; each great circle divides the surface of the sphere into two equal halves. Two great circles always intersect at two polar opposite points. Common examples of great circles are lines of longitude (meridians), which meet at the North and South Poles. Thus, the area between two meridians of longitude is a lune. The area of a spherical lune is 2θ R², where R is the radius of the sphere and θ is the dihedral angle between the two half great circles. When this angle equals 2π — i.e., when the second half great circle has moved a full circle, and the lune in between covers the sphere — the area formula for the spherical lune gives 4πR², the surface area of the sphere.

The crescent Moon is a spherical lune perceived as the intersection of a semicircle and semi-ellipse. Here, the blue and red portions may be taken equally as the sunlit and dark portions of the Moon visible from Earth or vice versa.

The lighted portion of the Moon visible from the Earth is a spherical lune. The first of the two intersecting great circles is the terminator between the sunlit half of the Moon and the dark half. The second great circle is that which separates the half visible from the Earth from the invisible half. This lighted spherical lune produces the familiar crescent shape of the Moon seen from Earth, the intersection of a semicircle and semi-ellipse (with the major axis of the ellipse coinciding with the diameter of the circle), as illustrated in the figure on the left.

Lune of Hippocrates

In the 5th century BC, Hippocrates of Chios showed that certain lunes, could be exactly squared by straightedge and compass. See Lune of Hippocrates.

See also

• Arbelos
• Spherical geometry
• Gauss–Bonnet theorem

References

1. ^ http://groups.google.com/group/geometry.college/browse_thread/thread/55e2a51789739627?pli=1
2. ^ Weisstein, Eric W., "SphericalLune" from MathWorld.

External links

• The Five Squarable Lunes at MathPages