Digon

Digon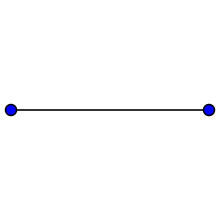
A degenerate digon with two coinciding edges sharing the same vertices
Edges and vertices	2
Schläfli symbol	{2}
Coxeter–Dynkin diagrams
Area	depends on geometric surface
Internal angle (degrees)	depends on geometric surface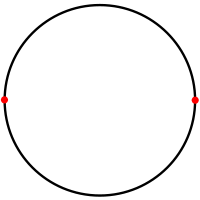

On a circle, a nondegenerate antipodal digon is a tessellation composed of two vertices and two 180 degree arcs.

In geometry, a digon is a polygon with two sides (edges) and two vertices. It is degenerate in a Euclidean space, but may be non-degenerate in a spherical space.

A digon must be regular because its two edges are the same length. It has Schläfli symbol {2}.

Some authorities do not consider the digon to be a proper polygon because of its degeneracy in the Euclidean case, but most formulae on general polygons do work on the digon. For example, the angle sum of an n-gon, (n − 2)π, would become 0 when n = 2, which is correct for a Euclidean digon.

In spherical tilings

In Euclidean geometry a digon is always degenerate. However, in spherical geometry a nondegenerate digon (with a nonzero interior area) can exist if the vertices are antipodal. The internal angle of the spherical digon vertex can be any angle between 0 and 180 degrees. Such a spherical polygon can also be called a lune.

• 

  One antipodal digon on the sphere.

• 

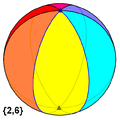
  Six antipodal digon faces on a hexagonal hosohedron tiling on the sphere.

In polyhedra

A digon is considered a degenerate face of a polyhedron because it has no geometric area and edges are overlapping. But sometimes it can have a useful topological existence in transforming polyhedra.

Any polyhedron can be topologically modified by replacing an edge with a digon. Such an operation adds one edge and one face to the polyhedron, although the result is geometrically identical. This transformation has no effect on the Euler characteristic (χ=V-E+F).

A digon face can also be created by geometrically collapsing a quadrilateral face by moving pairs of vertices to coincide in space. This digon can then be replaced by a single edge. It loses one face, two vertices, and three edges, again leaving the Euler characteristic unchanged.

Classes of polyhedra can be derived as degenerate forms of a primary polyhedron, with faces sometimes being degenerated into coinciding vertices. For example, this class of 7 uniform polyhedron with octahedral symmetry exist as degenerate forms of the truncated cuboctahedron (4.6.8). This principle is used in the Wythoff construction.

4.4.4

3.8.8

3.4.3.4

4.6.6

3.3.3.3

3.4.4.4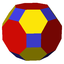

4.6.8

See also

• Dihedron - a degenerate polyhedron with 2 faces.
• Hosohedron - a degenerate polyhedron with 2 vertices.
• Demihypercube

References

• Weisstein, Eric W., "Digon" from MathWorld.
• A.B. Ivanov (2001), "Digon", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104, http://eom.springer.de/D/d032390.htm 

External links