Cube

This article is about the geometric shape. For other uses, see Cube (disambiguation).

Regular Hexahedron
(Click here for rotating model)
Type	Platonic solid
Elements	F = 6, E = 12 V = 8 (χ = 2)
Faces by sides	6{4}
Schläfli symbol	{4,3}
Wythoff symbol	3 | 2 4
Coxeter-Dynkin
Symmetry	Oh, [4,3], (*432)
References	U06, C18, W3
Properties	Regular convex zonohedron
Dihedral angle	90°
4.4.4 (Vertex figure)	Octahedron (dual polyhedron)
Net

In geometry, a cube^[1] is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and of trigonal trapezohedron. The cube is dual to the octahedron. It has cubical symmetry (also called octahedral symmetry). It is special by being a cuboid and a rhombohedron.

Cartesian coordinates

Orthographic projections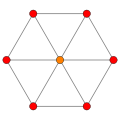

For a cube centered at the origin, with edges parallel to the axes and with an edge length of 2, the Cartesian coordinates of the vertices are

(±1, ±1, ±1)

while the interior consists of all points (x₀, x₁, x₂) with −1 < x _i < 1.

Formulae

For a cube of edge length a,

surface area	6a2
volume	a3
face diagonal	$\sqrt 2a$
space diagonal	$\sqrt 3a$
radius of circumscribed sphere	$\frac{\sqrt 3}{2} a$
radius of sphere tangent to edges	$\frac{a}{\sqrt 2}$
radius of inscribed sphere	$\frac{a}{2}$
angles between faces	$\frac{\pi}{2}$

As the volume of a cube is the third power of its sides a×a×a, third powers are called cubes, by analogy with squares and second powers.

A cube has the largest volume among cuboids (rectangular boxes) with a given surface area. Also, a cube has the largest volume among cuboids with the same total linear size(length+width+height).

Uniform colorings and symmetry

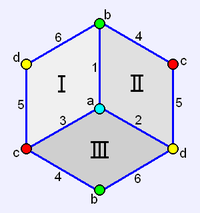
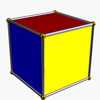
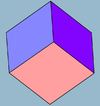
The cube has three uniform colorings, named by the colors of the square faces around each vertex: 111, 112, 123.

The cube has three classes of symmetry, which can be represented by vertex-transitive coloring the faces. The highest octahedral symmetry O_h has all the faces the same color. The dihedral symmetry D_4h comes from the cube being a prism, with all four sides being the same color. The lowest symmetry D_2h is also a prismatic symmetry, with sides alternating colors, so there are three colors, paired by opposite sides. Each symmetry form has a different Wythoff symbol.

Name	Regular hexahedron	Square prism	Cuboid	Trigonal trapezohedron
Coxeter-Dynkin
Schläfli symbol	{4,3}	{4}x{}	{}x{}x{}
Wythoff symbol	3 | 4 2	4 2 | 2	| 2 2 2
Symmetry	Oh (*432)	D4h (*422)	D2h (*222)	D3d (2*3)
Symmetry order	24	16	8	12
Image (uniform coloring)	(111)	(112)	(123)	(111), (112), (122), and (222)

Geometric relations

The 11 nets of the cube.

These familiar six-sided dice are cube-shaped.

A cube has 11 nets (one shown above): that is, there are 11 ways to flatten a hollow cube by cutting 7 edges.^[2] To colour the cube so that no two adjacent faces have the same colour, one would need at least 3 colours.

The cube is the cell of the only regular tiling of 3 dimensional Euclidean space. It is also unique among the Platonic solids in having faces with an even number of sides and, consequently, it is the only member of that group that is a zonohedron (every face has point symmetry).

The cube can be cut into 6 identical square pyramids. If these square pyramids are then attached to the faces of a second cube, a rhombic dodecahedron is obtained (with pairs of coplanar triangles combined into rhombic faces.)

Other dimensions

The analogue of a cube in four-dimensional Euclidean space has a special name—a tesseract or hypercube. More properly, a hypercube (or n-dimensional cube or simply n-cube) is the analogue of the cube in n-dimensional Euclidean space and a tesseract is the order-4 hypercube. A hypercube is also called a measure polytope.

There are analogues of the cube in lower dimensions too: a point in dimension 0, a segment in one dimension and a square in two dimensions.

Related polyhedra

The dual of a cube is an octahedron.

The hemicube is the 2-to-1 quotient of the cube.

The quotient of the cube by the antipodal map yields a projective polyhedron, the hemicube.

If the original cube has edge length 1, its dual polyhedron (an octahedron) has edge length $\sqrt{2}$.

The cube is a special case in various classes of general polyhedra:

Name	Equal edge-lengths?	Equal angles?	Right angles?
Cube	Yes	Yes	Yes
Rhombohedron	Yes	Yes	No
Cuboid	No	Yes	Yes
Parallelepiped	No	Yes	No
quadrilaterally faced hexahedron	No	No	No

The vertices of a cube can be grouped into two groups of four, each forming a regular tetrahedron; more generally this is referred to as a demicube. These two together form a regular compound, the stella octangula. The intersection of the two forms a regular octahedron. The symmetries of a regular tetrahedron correspond to those of a cube which map each tetrahedron to itself; the other symmetries of the cube map the two to each other.

One such regular tetrahedron has a volume of ⅓ of that of the cube. The remaining space consists of four equal irregular tetrahedra with a volume of 1/6 of that of the cube, each.

The rectified cube is the cuboctahedron. If smaller corners are cut off we get a polyhedron with 6 octagonal faces and 8 triangular ones. In particular we can get regular octagons (truncated cube). The rhombicuboctahedron is obtained by cutting off both corners and edges to the correct amount.

A cube can be inscribed in a dodecahedron so that each vertex of the cube is a vertex of the dodecahedron and each edge is a diagonal of one of the dodecahedron's faces; taking all such cubes gives rise to the regular compound of five cubes.

If two opposite corners of a cube are truncated at the depth of the 3 vertices directly connected to them, an irregular octahedron is obtained. Eight of these irregular octahedra can be attached to the triangular faces of a regular octahedron to obtain the cuboctahedron.

Related uniform polyhedra

Cube	Truncated cube	cuboctahedron	Truncated octahedron	Octahedron	Rhombi-cuboctahedron	truncated cuboctahedron	Snub cube	Stella octangula

All these figures have octahedral symmetry.

The cube is a part of a sequence of rhombic polyhedra and tilings with [n,3] Coxeter group symmetry. The cube can be seen as a rhombic hexahedron where the rhombi are squares.

Polyhedra			Euclidean tiling	Hyperbolic tiling
[3,3]	[4,3]	[5,3]	[6,3]	[7,3]	[8,3]
Cube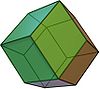	Rhombic dodecahedron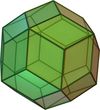	Rhombic triacontahedron	Rhombille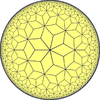

Regular and uniform compounds of cubes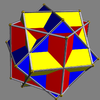

Compound of three cubes

Compound of five cubes

In uniform honeycombs and polychora

It is an element of 9 of 28 convex uniform honeycombs:

Cubic honeycomb	Truncated square prismatic honeycomb	Snub square prismatic honeycomb	Elongated triangular prismatic honeycomb	Gyroelongated triangular prismatic honeycomb
Cantellated cubic honeycomb	Cantitruncated cubic honeycomb	Runcitruncated cubic honeycomb	Runcinated alternated cubic honeycomb

It is also an element of five four-dimensional uniform polychora:

Tesseract	Cantellated 16-cell	Runcinated tesseract	Cantitruncated 16-cell	Runcitruncated 16-cell

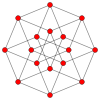
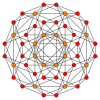
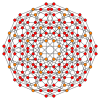
Combinatorial cubes

A different kind of cube is the cube graph, which is the graph of vertices and edges of the geometrical cube. It is a special case of the hypercube graph.

An extension is the three dimensional k-ary Hamming graph, which for k = 2 is the cube graph. Graphs of this sort occur in the theory of parallel processing in computers.

See also

• Unit cube
• Tesseract
• Cube (film)
• Trapezohedron
• Yoshimoto Cube
• The Cube (game show)
• Prince Rupert's cube
• OLAP cube

References

1. ^ English cube from Old French < Latin cubus < Greek kubos meaning "a cube, a die, vertebra". In turn from PIE *keu(b)-, "to bend, turn".
2. ^ Weisstein, Eric W., "Cube" from MathWorld.

External links

• Weisstein, Eric W., "Cube" from MathWorld.
• Richard Klitzing, 3D convex uniform polyhedra, o3o4x - cube
• Editable printable net of a cube with interactive 3D view
• Cube: Interactive Polyhedron Model
• K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
• The Uniform Polyhedra
• Virtual Reality Polyhedra
• Volume of a cube, with interactive animation