Tetrahedron

For the academic journal, see Tetrahedron (journal).

Regular Tetrahedron
(Click here for rotating model)
Type	Platonic solid
Elements	F = 4, E = 6 V = 4 (χ = 2)
Faces by sides	4{3}
Schläfli symbol	{3,3} and s{2,2}
Wythoff symbol	3 | 2 3 | 2 2 2
Coxeter-Dynkin
Symmetry	Td, [3,3], (*332)
References	U01, C15, W1
Properties	Regular convex deltahedron
Dihedral angle	70.528779° = arccos(1/3)
3.3.3 (Vertex figure)	Self-dual (dual polyhedron)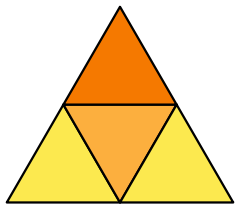
Net

In geometry, a tetrahedron (plural: tetrahedra) is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids. The tetrahedron is the only convex polyhedron that has four faces.^[1]

The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex.

The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a triangular pyramid.

Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two nets.^[1]

For any tetrahedron there exists a sphere (the circumsphere) such that the tetrahedron's vertices lie on the sphere's surface.

Formulas for regular tetrahedron

For a regular tetrahedron of edge length a:

Base plane area	$A_0={\sqrt{3}\over4}a^2 \,$
Surface area[2]	$A=4\,A_0={\sqrt{3}}a^2 \,$
Height [3]	$H={\sqrt{6}\over3}a \,$
Volume[2]	$V={1\over3} A_0h ={\sqrt{2}\over12}a^3 \,$
Angle between an edge and a face	$\arccos\left({1 \over \sqrt{3}}\right) = \arctan(\sqrt{2}) \,$ (approx. 54.7356°)
Angle between two faces[2]	$\arccos\left({1 \over 3}\right) = \arctan(2\sqrt{2}) \,$ (approx. 70.5288°)
Angle between the segments joining the center and the vertices,[4] also known as the tetrahedral angle	$\arccos\left ({-1\over3}\right ) = 2\arctan(\sqrt{2}) \,$ (approx. 109.4712°)
Solid angle at a vertex subtended by a face	$\arccos\left ({23\over27}\right )$ (approx. 0.55129 steradians)
Radius of circumsphere[2]	$R=\sqrt{{3\over8}}\,a \,$
Radius of insphere that is tangent to faces[2]	$r={1\over3}R={a\over\sqrt{24}} \,$
Radius of midsphere that is tangent to edges[2]	$r_M=\sqrt{rR}={a\over\sqrt{8}} \,$
Radius of exspheres	$r_E={a\over\sqrt{6}} \,$
Distance to exsphere center from a vertex	$\sqrt{{3\over2}}\,a \,$

Note that with respect to the base plane the slope of a face ($2 \sqrt{2}$) is twice that of an edge ($\sqrt{2}$), corresponding to the fact that the horizontal distance covered from the base to the apex along an edge is twice that along the median of a face. In other words, if C is the centroid of the base, the distance from C to a vertex of the base is twice that from C to the midpoint of an edge of the base. This follows from the fact that the medians of a triangle intersect at its centroid, and this point divides each of them in two segments, one of which is twice as long as the other (see proof).

Volume

The volume of a tetrahedron is given by the pyramid volume formula:

$V = \frac{1}{3} A_0\,h \,$

where A₀ is the area of the base and h the height from the base to the apex. This applies for each of the four choices of the base, so the distances from the apexes to the opposite faces are inversely proportional to the areas of these faces.

For a tetrahedron with vertices a = (a₁, a₂, a₃), b = (b₁, b₂, b₃), c = (c₁, c₂, c₃), and d = (d₁, d₂, d₃), the volume is (1/6)·|det(a−b, b−c, c−d)|, or any other combination of pairs of vertices that form a simply connected graph. This can be rewritten using a dot product and a cross product, yielding

$V = \frac { |(\mathbf{a}-\mathbf{d}) \cdot ((\mathbf{b}-\mathbf{d}) \times (\mathbf{c}-\mathbf{d}))| } {6}.$

If the origin of the coordinate system is chosen to coincide with vertex d, then d = 0, so

$V = \frac { |\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})| } {6},$

where a, b, and c represent three edges that meet at one vertex, and $\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})$ is a scalar triple product. Comparing this formula with that used to compute the volume of a parallelepiped, we conclude that the volume of a tetrahedron is equal to 1/6 of the volume of any parallelepiped that shares three converging edges with it.

The triple scalar can be represented by the following determinants:

$6 \cdot V =\begin{vmatrix} \mathbf{a} & \mathbf{b} & \mathbf{c} \end{vmatrix}$    or    $6 \cdot V =\begin{vmatrix} \mathbf{a} \\ \mathbf{b} \\ \mathbf{c} \end{vmatrix}$    where    $\mathbf{a} = (a_1,a_2,a_3) \,$    is expressed as a row or column vector etc.

Hence

$36 \cdot V^2 =\begin{vmatrix} \mathbf{a^2} & \mathbf{a} \cdot \mathbf{b} & \mathbf{a} \cdot \mathbf{c} \\ \mathbf{a} \cdot \mathbf{b} & \mathbf{b^2} & \mathbf{b} \cdot \mathbf{c} \\ \mathbf{a} \cdot \mathbf{c} & \mathbf{b} \cdot \mathbf{c} & \mathbf{c^2} \end{vmatrix}$    where    $\mathbf{a} \cdot \mathbf{b} = ab\cos{\gamma}$    etc.

which gives

$V = \frac {abc} {6} \sqrt{1 + 2\cos{\alpha}\cos{\beta}\cos{\gamma}-\cos^2{\alpha}-\cos^2{\beta}-\cos^2{\gamma}}, \,$

where $\alpha,\beta,\gamma\,$ are the plane angles occurring in vertex d. The angle $\alpha\,$ is the angle between the two edges connecting the vertex d to the vertices b and c. The angle $\beta\,$ does so for the vertices a and c, while $\gamma\,$ is defined by the position of the vertices a and b.

Given the distances between the vertices of a tetrahedron the volume can be computed using the Cayley–Menger determinant:

$288 \cdot V^2 = \begin{vmatrix} 0 & 1 & 1 & 1 & 1 \\ 1 & 0 & d_{12}^2 & d_{13}^2 & d_{14}^2 \\ 1 & d_{12}^2 & 0 & d_{23}^2 & d_{24}^2 \\ 1 & d_{13}^2 & d_{23}^2 & 0 & d_{34}^2 \\ 1 & d_{14}^2 & d_{24}^2 & d_{34}^2 & 0 \end{vmatrix}$

where the subscripts $i,\,j\in\{1,\,2,\,3,\,4\}$ represent the vertices $\{\mathbf{a},\mathbf{b},\mathbf{c},\mathbf{d}\}$ and $d_{ij}\,$ is the pairwise distance between them—i.e., the length of the edge connecting the two vertices. A negative value of the determinant means that a tetrahedron cannot be constructed with the given distances. This formula, sometimes called Tartaglia's formula, is essentially due to the painter Piero della Francesca in the 15th century, as a three dimensional analogue of the 1st century Heron's formula for the area of a triangle.^[5]

Distance between the edges

Any two opposite edges of a tetrahedron lie on two skew lines. If the closest pair of points between these two lines are points in the edges, they define the distance between the edges; otherwise, the distance between the edges equals that between one of the endpoints and the opposite edge. Let d be the distance between the skew lines formed by opposite edges a and b-c as calculated in.^[6] Then another volume formula is given by

$V = \frac { d |(\mathbf{a} \times \mathbf{(b-c)})| } {6}.$

Properties of a generalized tetrahedron

The tetrahedron has many properties analogous to those of a triangle, including an insphere, circumsphere, medial tetrahedron, and exspheres. It has respective centers such as incenter, circumcenter, excenters, Spieker center and points such as a centroid. However, there is generally no orthocenter in the sense of intersecting altitudes. The circumsphere of the medial tetrahedron is analogous to the triangle's nine point circle, but does not generally pass through the base points of the altitudes of the reference tetrahedron.^[7]

Gaspard Monge found a 'center' that exists in every tetrahedron, now known as the Monge point: the point where the six midplanes of a tetrahedron intersect. A midplane is defined as a plane that is orthogonal to an edge joining any two vertices that also contains the centroid of an opposite edge formed by joining the other two vertices. If the tetrahedron's altitudes do intersect, the Monge point and the orthocenter coincide.

An orthogonal line dropped from the Monge point to any face meets that face at the midpoint of the line segment between that face's orthocenter and the foot of the altitude dropped from the opposite vertex.

The centroid of a tetrahedron lies at the midpoint of its Monge point and circumcenter, on the Euler line of the tetrahedron.

The nine-point circle of the general triangle has an analogue in the circumsphere of a tetrahedron's medial tetrahedron. It is the twelve-point sphere and besides the centroids of the four faces of the reference tetrahedron, it passes through four substitute Euler points, 1/3 of the way from the Monge point toward each of the four vertices. Finally it passes through the four base points of orthogonal lines dropped from each Euler point to the face not containing the vertex that generated the Euler point.^[8]

The center T of the twelve-point sphere also lies on the Euler line. Unlike its triangular counterpart, this center lies 1/3 of the way from the Monge point M towards the circumcenter. Also, an orthogonal line through T to a chosen face is coplanar with two other orthogonal lines to the same face. The first is an orthogonal line passing through the corresponding Euler point to the chosen face. The second is an orthogonal line passing through the centroid of the chosen face. This orthogonal line through the twelve-point center lies midway between the Euler point orthogonal line and the centroidal orthogonal line. Furthermore, for any face, the twelve-point center lies at the mid point of the corresponding Euler point and the orthocenter for that face.

The radius of the twelve-point sphere is 1/3 of the circumradius of the reference tetrahedron.

If OABC forms a generalized tetrahedron with a vertex O as the origin and vectors $\mathbf{a}, \mathbf{b} \,$ and $\mathbf{c} \,$ represent the positions of the vertices A, B, and C with respect to O, then the radius of the insphere is given by^{[citation needed]}:

$r= \frac {6V} {|\mathbf{b} \times \mathbf{c}| + |\mathbf{c} \times \mathbf{a}| + |\mathbf{a} \times \mathbf{b}| + |(\mathbf{b} \times \mathbf{c}) + (\mathbf{c} \times \mathbf{a}) + (\mathbf{a} \times \mathbf{b})|} \,$

and the radius of the circumsphere is given by:

$R= \frac {|\mathbf{a^2}(\mathbf{b} \times \mathbf{c}) + \mathbf{b^2}(\mathbf{c} \times \mathbf{a}) + \mathbf{c^2}(\mathbf{a} \times \mathbf{b})|} {12V} \,$

which gives the radius of the twelve-point sphere:

$r_T= \frac {|\mathbf{a^2}(\mathbf{b} \times \mathbf{c}) + \mathbf{b^2}(\mathbf{c} \times \mathbf{a}) + \mathbf{c^2}(\mathbf{a} \times \mathbf{b})|} {36V} \,$

where:

$6V= |\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})|. \,$

In the formulas throughout this section, the scalar a² represents the inner vector product a·a; similarly b² and c².

The vector positions of various centers are as follows:

The centroid

$\mathbf{G} = \frac{\mathbf{a} + \mathbf{b} + \mathbf{c}}{4}. \,$

The incenter

$\mathbf{I}= \frac{ \mathbf{a} \cdot |\mathbf{b}\times \mathbf{c}| + \mathbf{b} \cdot |\mathbf{c}\times \mathbf{a}| + \mathbf{c} \cdot |\mathbf{a}\times \mathbf{b}| }{ |\mathbf{b}\times \mathbf{c}| + |\mathbf{c}\times \mathbf{a}| + |\mathbf{a}\times \mathbf{b}| + |\mathbf{b}\times \mathbf{c} + \mathbf{c}\times \mathbf{a} + \mathbf{a}\times \mathbf{b}| }. \,$

The circumcenter

$\mathbf{O}= \frac {\mathbf{a^2}(\mathbf{b} \times \mathbf{c}) + \mathbf{b^2}(\mathbf{c} \times \mathbf{a}) + \mathbf{c^2}(\mathbf{a} \times \mathbf{b})} {2\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})}. \,$

The Monge point

$\mathbf{M} = \frac {\mathbf{a} \cdot (\mathbf{b} + \mathbf{c})(\mathbf{b} \times \mathbf{c}) + \mathbf{b}\cdot (\mathbf{c} + \mathbf{a})(\mathbf{c} \times \mathbf{a}) + \mathbf{c} \cdot (\mathbf{a} + \mathbf{b})(\mathbf{a} \times \mathbf{b})} {2\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})}. \,$

The Euler line relationships are:

$\mathbf{G} = \mathbf{M} + \frac{1}{2} (\mathbf{O}-\mathbf{M})\,$

$\mathbf{T} = \mathbf{M} + \frac{1}{3} (\mathbf{O}-\mathbf{M})\,$

where $\mathbf{T}\,$ is twelve-point center.

Also:

$\mathbf{a} \cdot \mathbf{O} = \frac {\mathbf{a^2}}{2} \quad\quad \mathbf{b} \cdot \mathbf{O} = \frac {\mathbf{b^2}}{2} \quad\quad \mathbf{c} \cdot \mathbf{O} = \frac {\mathbf{c^2}}{2}\,$

and:

$\mathbf{a} \cdot \mathbf{M} = \frac {\mathbf{a} \cdot (\mathbf{b} + \mathbf{c})}{2} \quad\quad \mathbf{b} \cdot \mathbf{M} = \frac {\mathbf{b} \cdot (\mathbf{c} + \mathbf{a})}{2} \quad\quad \mathbf{c} \cdot \mathbf{M} = \frac {\mathbf{c} \cdot (\mathbf{a} + \mathbf{b})}{2}.\,$

Geometric relations

A tetrahedron is a 3-simplex. Unlike the case of the other Platonic solids, all the vertices of a regular tetrahedron are equidistant from each other (they are the only possible arrangement of four equidistant points in 3-dimensional space).

A tetrahedron is a triangular pyramid, and the regular tetrahedron is self-dual.

A regular tetrahedron can be embedded inside a cube in two ways such that each vertex is a vertex of the cube, and each edge is a diagonal of one of the cube's faces. For one such embedding, the Cartesian coordinates of the vertices are

(+1, +1, +1);

(−1, −1, +1);

(−1, +1, −1);

(+1, −1, −1).

This yields a tetrahedron with edge-length 2√2, centered at the origin. For the other tetrahedron (which is dual to the first), reverse all the signs. These two tetrahedra's vertices combined are the vertices of a cube, demonstrating that the regular tetrahedron is the 3-demicube.

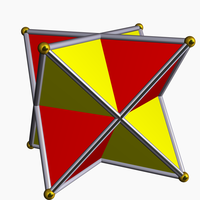The stella octangula.

The volume of this tetrahedron is 1/3 the volume of the cube. Combining both tetrahedra gives a regular polyhedral compound called the compound of two tetrahedra or stella octangula.

The interior of the stella octangula is an octahedron, and correspondingly, a regular octahedron is the result of cutting off, from a regular tetrahedron, four regular tetrahedra of half the linear size (i.e., rectifying the tetrahedron).

The above embedding divides the cube into five tetrahedra, one of which is regular. In fact, 5 is the minimum number of tetrahedra required to compose a cube.

Inscribing tetrahedra inside the regular compound of five cubes gives two more regular compounds, containing five and ten tetrahedra.

Regular tetrahedra cannot tessellate space by themselves, although this result seems likely enough that Aristotle claimed it was possible. However, two regular tetrahedra can be combined with an octahedron, giving a rhombohedron that can tile space.

However, there is at least one irregular tetrahedron of which copies can tile space. If one relaxes the requirement that the tetrahedra be all the same shape, one can tile space using only tetrahedra in various ways. For example, one can divide an octahedron into four identical tetrahedra and combine them again with two regular ones. (As a side-note: these two kinds of tetrahedron have the same volume.)

The tetrahedron is unique among the uniform polyhedra in possessing no parallel faces.

Related polyhedra

• 

  Truncated tetrahedron

• 

  Two tetrahedra in a cube

• 

  Compound of five tetrahedra

• 

  Compound of ten tetrahedra

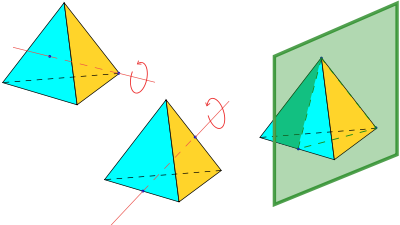
A truncation process applied to the tetrahedron produces a series of uniform polyhedra. Truncating edges down to points produces the octahedron as a rectified tetahedron. The process completes as a birectification, reducing the original faces down to points, and producing the self-dual tetrahedron once again.

Name	tetrahedron	rectified tetrahedron (octahedron)	truncated tetrahedron	cantellated tetrahedron (cuboctahedron)	omnitruncated tetrahedron (truncated octahedron)	Snub tetrahedron (icosahedron)
Schläfli	{3,3}	t1{3,3}	t0,1{3,3}	t0,2{3,3}	t0,1,2{3,3}	s{3,3}
Coxeter-Dynkin
Graph (A3)
Graph (A2)
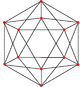
Solid
Tiling

This polyhedron is topologically related as a part of sequence of regular polyhedra with Schläfli symbols {3,n}, continuing into the hyperbolic plane.

{3,3}

{3,4}

{3,5}

{3,6}

{3,7}

{3,8}

{3,9}

Intersecting tetrahedra

An interesting polyhedron can be constructed from five intersecting tetrahedra. This compound of five tetrahedra has been known for hundreds of years. It comes up regularly in the world of origami. Joining the twenty vertices would form a regular dodecahedron. There are both left-handed and right-handed forms, which are mirror images of each other.

Isometries

Isometries of regular tetrahedra

The proper rotations and reflections in the symmetry group of the regular tetrahedron

The vertices of a cube can be grouped into two groups of four, each forming a regular tetrahedron (see above, and also animation, showing one of the two tetrahedra in the cube). The symmetries of a regular tetrahedron correspond to half of those of a cube: those that map the tetrahedrons to themselves, and not to each other.

The tetrahedron is the only Platonic solid that is not mapped to itself by point inversion.

The regular tetrahedron has 24 isometries, forming the symmetry group T_d, isomorphic to S₄. They can be categorized as follows:

• T, isomorphic to alternating group A₄ (the identity and 11 proper rotations) with the following conjugacy classes (in parentheses are given the permutations of the vertices, or correspondingly, the faces, and the unit quaternion representation):
  • identity (identity; 1)
  • rotation about an axis through a vertex, perpendicular to the opposite plane, by an angle of ±120°: 4 axes, 2 per axis, together 8 ((1 2 3), etc.; (1 ± i ± j ± k)/2)
  • rotation by an angle of 180° such that an edge maps to the opposite edge: 3 ((1 2)(3 4), etc.; i, j, k)
• reflections in a plane perpendicular to an edge: 6
• reflections in a plane combined with 90° rotation about an axis perpendicular to the plane: 3 axes, 2 per axis, together 6; equivalently, they are 90° rotations combined with inversion (x is mapped to −x): the rotations correspond to those of the cube about face-to-face axes

Isometries of irregular tetrahedra

The isometries of an irregular tetrahedron depend on the geometry of the tetrahedron, with 7 cases possible. In each case a 3-dimensional point group is formed.

• An equilateral triangle base and isosceles (and non-equilateral) triangle sides gives 6 isometries, corresponding to the 6 isometries of the base. As permutations of the vertices, these 6 isometries are the identity 1, (123), (132), (12), (13) and (23), forming the symmetry group C_3v, isomorphic to S₃.
• Four congruent isosceles (non-equilateral) triangles gives 8 isometries. If edges (1,2) and (3,4) are of different length to the other 4 then the 8 isometries are the identity 1, reflections (12) and (34), and 180° rotations (12)(34), (13)(24), (14)(23) and improper 90° rotations (1234) and (1432) forming the symmetry group D_2d.
• Four congruent scalene triangles gives 4 isometries. The isometries are 1 and the 180° rotations (12)(34), (13)(24), (14)(23). This is the Klein four-group V₄ ≅ Z₂², present as the point group D₂. A tetrahedron with this symmetry is called disphenoid.
• Two pairs of isomorphic isosceles (non-equilateral) triangles. This gives two opposite edges (1,2) and (3,4) that are perpendicular but different lengths, and then the 4 isometries are 1, reflections (12) and (34) and the 180° rotation (12)(34). The symmetry group is C_2v, isomorphic to V₄.
• Two pairs of isomorphic scalene triangles. This has two pairs of equal edges (1,3), (2,4) and (1,4), (2,3) but otherwise no edges equal. The only two isometries are 1 and the rotation (12)(34), giving the group C₂ isomorphic to Z₂.
• Two unequal isosceles triangles with a common base. This has two pairs of equal edges (1,3), (1,4) and (2,3), (2,4) and otherwise no edges equal. The only two isometries are 1 and the reflection (34), giving the group C_s isomorphic to Z₂.
• No edges equal, so that the only isometry is the identity, and the symmetry group is the trivial group.

A law of sines for tetrahedra and the space of all shapes of tetrahedra

A corollary of the usual law of sines is that in a tetrahedron with vertices O, A, B, C, we have

$\sin\angle OAB\cdot\sin\angle OBC\cdot\sin\angle OCA = \sin\angle OAC\cdot\sin\angle OCB\cdot\sin\angle OBA.\,$

One may view the two sides of this identity as corresponding to clockwise and counterclockwise orientations of the surface.

Putting any of the four vertices in the role of O yields four such identities, but in a sense at most three of them are independent: If the "clockwise" sides of three of them are multiplied and the product is inferred to be equal to the product of the "counterclockwise" sides of the same three identities, and then common factors are cancelled from both sides, the result is the fourth identity. One reason to be interested in this "independence" relation is this: It is widely known that three angles are the angles of some triangle if and only if their sum is a half-circle. What condition on 12 angles is necessary and sufficient for them to be the 12 angles of some tetrahedron? Clearly the sum of the angles of any side of the tetrahedron must be a half-circle. Since there are four such triangles, there are four such constraints on sums of angles, and the number of degrees of freedom is thereby reduced from 12 to 8. The four relations given by this sine law further reduce the number of degrees of freedom, not from 8 down to 4, but only from 8 down to 5, since the fourth constraint is not independent of the first three. Thus the space of all shapes of tetrahedra is 5-dimensional.

Applications

The ammonium+ ion is tetrahedral

4-sided die

Numerical analysis

In numerical analysis, complicated three-dimensional shapes are commonly broken down into, or approximated by, a polygonal mesh of irregular tetrahedra in the process of setting up the equations for finite element analysis especially in the numerical solution of partial differential equations. These methods have wide applications in practical applications in computational fluid dynamics, aerodynamics, electromagnetic fields, civil engineering, chemical engineering, naval architecture and engineering, and related fields.

Chemistry

The tetrahedron shape is seen in nature in covalent bonds of molecules. All sp³-hybridized atoms are surrounded by atoms lying in each corner of a tetrahedron. For instance in a methane molecule (CH₄) or an ammonium ion (NH₄⁺), four hydrogen atoms surround a central carbon or nitrogen atom with tetrahedral symmetry. For this reason, one of the leading journals in organic chemistry is called Tetrahedron. See also tetrahedral molecular geometry. The central angle between any two vertices of a perfect tetrahedron is $\arccos{\left(-\tfrac{1}{3}\right)}$, or approximately 109.47°).

Water, H₂O, also has a tetrahedral structure, with two hydrogen atoms and two lone pairs of electrons around the central oxygen atoms. Its tetrahedral symmetry is not perfect, however, because the lone pairs repel more than the single O-H bonds.

Quaternary phase diagrams in chemistry are represented graphically as tetrahedra.

However, quaternary phase diagrams in communication engineering are represented graphically on a two-dimensional plane.

Electricity and electronics

If six equal resistors are soldered together to form a tetrahedron, then the resistance measured between any two vertices is half that of one resistor.^[9][10]

Since silicon is the most common semiconductor used in solid-state electronics, and silicon has a valence of four, the tetrahedral shape of the four chemical bonds in silicon is a strong influence on how crystals of silicon form and what shapes they assume.

Games

Especially in roleplaying, this solid is known as a 4-sided die, one of the more common polyhedral dice, with the number rolled appearing around the bottom or on the top vertex. Some Rubik's Cube-like puzzles are tetrahedral, such as the Pyraminx and Pyramorphix.

Color space

Tetrahedra are used in color space conversion algorithms specifically for cases in which the luminance axis diagonally segments the color space (e.g. RGB, CMY).^[11]

Contemporary Art

The Austrian artist Martina Schettina created a tetrahedron using fluorescent lamps. It was shown at the light art biennale Austria 2010.^[12]

It is used as album artwork, surrounded by black flames on The End of All Things to Come by Mudvayne.

Geology

The tetrahedral hypothesis, originally published by William Lowthian Green to explain the formation of the Earth,^[13] was popular through the early 20th century.^[14][15]

See also

• Boerdijk–Coxeter helix
• Caltrop
• Demihypercube
• Disphenoid — a tetrahedron with mirror symmetry
• Hill tetrahedron
• Simplex
• Tetra-Pak
• Tetrahedral kite
• Tetrahedral number
• Triangular dipyramid — constructed by joining two tetrahedra along one face
• Tetrahedron packing

References

1. ^ ^{a b} Weisstein, Eric W., "Tetrahedron" from MathWorld.
2. ^ ^{a b c d e f} Coxeter, H. S. M.: Regular Polytopes (Methuen and Co., 1948). Table I(i).
3. ^ http://www.mathematische-basteleien.de/tetrahedron.htm
4. ^ "Angle Between 2 Legs of a Tetrahedron" – Maze5.net
5. ^ http://www.mathpages.com/home/kmath424.htm
6. ^ http://en.wikipedia.org/wiki/Skew_lines#Distance_between_two_skew_lines</a>
7. ^ Havlicek, H.; Weiß, G. (2003). "Altitudes of a tetrahedron and traceless quadratic forms". American Mathematical Monthly 110 (8): 679–693.. doi:10.2307/3647851. JSTOR 3647851. http://www.geometrie.tuwien.ac.at/havlicek/pub/hoehen.pdf. 
8. ^ Outudee, Somluck; New, Stephen. The Various Kinds of Centres of Simplices. Dept of Maths., Chulalongkorn University, Bangkok. http://www.math.sc.chula.ac.th/ICAA2002/pages/Somluck_Outudee.pdf. ^{[dead link]}
9. ^ Klein, Douglas J. (2002). "Resistance-Distance Sum Rules" (PDF). Croatica Chemica Acta 75 (2): 633–649. http://jagor.srce.hr/ccacaa/CCA-PDF/cca2002/v75-n2/CCA_75_2002_633_649_KLEIN.pdf. Retrieved 2006-09-15. 
10. ^ Tomáš Záležák (18 October 2007). Resistance of a regular tetrahedron (PDF). Retrieved 25 Jan 2011.
11. ^ Vondran, Gary L. (April 1998). "Radial and Pruned Tetrahedral Interpolation Techniques" (PDF). HP Technical Report HPL-98-95: 1–32. http://www.hpl.hp.com/techreports/98/HPL-98-95.pdf. 
12. ^ Lightart-Biennale Austria 2010
13. ^ William Lowthian Green (1875). Vestiges of the Molten Globe, as exhibited in the figure of the earth, volcanic action and physiography. Part I. London: E. Stanford. OCLC 3571917. http://books.google.com/books?id=9DkDAAAAQAAJ. 
14. ^ Arthur Holmes (1965). Principles of physical geology. Nelson. p. 32. http://books.google.com/books?id=XUJRAAAAMAAJ. 
15. ^ Charles Henry Hitchcock (January 1900). "William Lowthian Green and his Theory of the Evolution of the Earth's Features". The American geologist (Geological Publishing Company) XXV: pp. 1–10. http://books.google.com/books?id=_Ty8AAAAIAAJ&pg=PA1. 

External links

• F. M. Jackson and Weisstein, Eric W., "Tetrahedron" from MathWorld.
• Weisstein, Eric W., "Monge point" from MathWorld.
• Weisstein, Eric W., "Euler points" from MathWorld.
• Richard Klitzing, 3D convex uniform polyhedra, x3o3o - tet
• The Uniform Polyhedra
• Editable printable net of a tetrahedron with interactive 3D view
• Tetrahedron: Interactive Polyhedron Model
• Piero della Francesca's formula for tetrahedron volume at MathPages
• Free paper models of a tetrahedron and many other polyhedra
• An Amazing, Space Filling, Non-regular Tetrahedron that also includes a description of a "rotating ring of tetrahedra", also known as a kaleidocycle.
• Tetrahedron Core Network Application of a tetrahedral structure to create resilient partial-mesh data network
• Explicit exact formulas for the inertia tensor of an arbitrary tetrahedron in terms of its vertex coordinates
• The inertia tensor of a tetrahedron