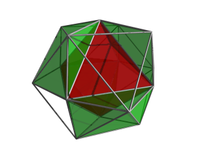
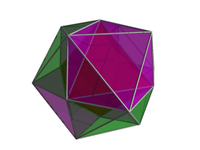
- 24-cell
-
24-cell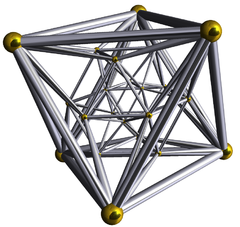 
Schlegel diagram
(vertices and edges)Type Convex regular 4-polytope Schläfli symbol {3,4,3}
t1{3,3,4}
t1{31,1,1}Coxeter-Dynkin diagram 
Cells 24 {3,4} 
Faces 96 {3} Edges 96 Vertices 24 Vertex figure Cube Petrie polygon dodecagon Coxeter group F4, [3,4,3] o(1152)
B4, [4,3,3] o(384)
D4, [31,1,1] o(192)Dual Self-dual Properties convex, isogonal, isotoxal, isohedral Uniform index 22 In geometry, the 24-cell (or icositetrachoron) is the convex regular 4-polytope, or polychoron, with Schläfli symbol {3,4,3}. It is also called an octaplex (short for "octahedral complex"), octacube, or polyoctahedron, being constructed of octahedral cells.
The boundary of the 24-cell is composed of 24 octahedral cells with six meeting at each vertex, and three at each edge. Together they have 96 triangular faces, 96 edges, and 24 vertices. The vertex figure is a cube. The 24-cell is self-dual. In fact, the 24-cell is the unique self-dual regular Euclidean polytope which is neither a polygon nor a simplex. Due to this singular property, it does not have a good analogue in 3 dimensions, but in 2 dimensions the hexagon, along with all regular polygons, are self-dual.
Contents
Constructions
A 24-cell is given as the convex hull of its vertices. The vertices of a 24-cell centered at the origin of 4-space, with edges of length 1, can be given as follows: 8 vertices obtained by permuting
- (±1, 0, 0, 0)
and 16 vertices of the form
- (±½, ±½, ±½, ±½).
The first 8 vertices are the vertices of a regular 16-cell and the other 16 are the vertices of the dual tesseract. This gives a construction equivalent to cutting a tesseract into 8 cubical pyramids, and then attaching them to the facets of a second tesseract. The analogous construction in 3-space gives the rhombic dodecahedron which, however, is not regular.
We can further divide the last 16 vertices into two groups: those with an even number of minus (−) signs and those with an odd number. Each of groups of 8 vertices also define a regular 16-cell. The vertices of the 24-cell can then be grouped into three sets of eight with each set defining a regular 16-cell, and with the complement defining the dual tesseract.
The vertices of the dual 24-cell are given by all permutations of
- (±1, ±1, 0, 0).
The dual 24-cell has edges of length √2 and is inscribed in a 3-sphere of radius √2.
Another method of constructing the 24-cell is by the rectification of the 16-cell. The vertex figure of the 16-cell is the octahedron; thus, cutting the vertices of the 16-cell at the midpoint of its incident edges produce 8 octahedral cells. This process also rectifies the tetrahedral cells of the 16-cell which also become octahedra, thus forming the 24 octahedral cells of the 24-cell.
Tessellations
A regular tessellation of 4-dimensional Euclidean space exists with 24-cells, called an icositetrachoric honeycomb, with Schläfli symbol {3,4,3,3}. The regular dual tessellation, {3,3,4,3} has 16-cells. (See also List of regular polytopes which includes a third regular tessellation, the tesseractic honeycomb {4,3,3,4}.)
Symmetries, root systems, and tessellations
The 24 vertices of the 24-cell (red nodes), and of its dual (yellow nodes), represent the 48 root vectors of the F4 group, as shown in this F4 Coxeter plane projection
The 24 vertices of the 24-cell represent the root vectors of the simple Lie group D4. When combined with the 8 vertices of the 16-cell these vertices represent the 32 root vectors of the simple Lie group B4.
The 48 vertices (or strictly speaking their radius vectors) of the 24-cell and its dual form the root system of type F4. The 24 vertices of the original 24-cell as well as the 24 vertices of the dual form root systems of type D4; their sizes have the ratio sqrt(2):1. The full symmetry group of the 24-cell is the Weyl group of F4 which is generated by reflections through the hyperplanes orthogonal to the F4 roots. This is a solvable group of order 1152. The rotational symmetry group of the 24-cell is of order 576.
When interpreted as the quaternions, the F4 root lattice (which is integral span of the vertices of the 24-cell) is closed under multiplication and is therefore forms a ring. This is the ring of Hurwitz integral quaternions. The vertices of the 24-cell form the group of units (i.e. the group of invertible elements) in the Hurwitz quaternion ring (this group is also known as the binary tetrahedral group). The vertices of the 24-cell are precisely the 24 Hurwitz quaternions with norm squared 1, and the vertices of the dual 24-cell are those with norm squared 2. The D4 root lattice is the dual of the F4 and is given by the subring of Hurwitz quaternions with even norm squared.
The Voronoi cells of the D4 root lattice are regular 24-cells. The corresponding Voronoi tessellation gives a tessellation of 4-dimensional Euclidean space by regular 24-cells. The 24-cells are centered at the D4 lattice points (Hurwitz quaternions with even norm squared) while the vertices are at the F4 lattice points with odd norm squared. Each 24-cell has 24 neighbors with which it shares an octahedron and 32 neighbors with which it shares only a single point. Eight 24-cells meet at any given vertex in this tessellation. The Schläfli symbol for this tessellation is {3,4,3,3}. The dual tessellation, {3,3,4,3}, is one by regular 16-cells. Together with the regular tesseract tessellation, {4,3,3,4}, these are the only regular tessellations of R4.
It is interesting to note that the unit balls inscribed in the 24-cells of the above tessellation give rise to the densest lattice packing of hyperspheres in 4 dimensions. The vertex configuration of the 24-cell has also been shown to give the highest possible kissing number in 4 dimensions.
Quaternions
Translating the four-dimensional coordinates into quaternions, the points of an appropriately scaled and orientated 24-cell form a multiplicative group. This property applies to two other regular polychora, namely the 16-cell and 600-cell, with 8 and 120 points, respectively. The group of 120 points is known as the icosian group.
Projections
Projection envelopes of the 24-cell. (Each cell is drawn with different colored faces, inverted cells are undrawn)The vertex-first parallel projection of the 24-cell into 3-dimensional space has a rhombic dodecahedral envelope. Twelve of the 24 octahedral cells project in pairs onto six square dipyramids that meet at the center of the rhombic dodecahedron. The remaining 12 octahedral cells project onto the 12 rhombic faces of the rhombic dodecahedron.
The cell-first parallel projection of the 24-cell into 3-dimensional space has a cuboctahedral envelope. Two of the octahedral cells, the nearest and farther from the viewer along the W-axis, project onto an octahedron whose vertices lie at the center of the cuboctahedron's square faces. Surrounding this central octahedron lie the projections of 16 other cells, having 8 pairs that each project to one of the 8 volumes lying between a triangular face of the central octahedron and the closest triangular face of the cuboctahedron. The remaining 6 cells project onto the square faces of the cuboctahedron. This corresponds with the decomposition of the cuboctahedron into a regular octahedron and 8 irregular but equal octahedra, each of which is in the shape of the convex hull of a cube with two opposite vertices removed.
The edge-first parallel projection has an elongated hexagonal dipyramidal envelope, and the face-first parallel projection has a nonuniform hexagonal bi-antiprismic envelope.
The vertex-first perspective projection of the 24-cell into 3-dimensional space has a tetrakis hexahedral envelope. The layout of cells in this image is similar to the image under parallel projection.
The following sequence of images shows the structure of the cell-first perspective projection of the 24-cell into 3 dimensions. The 4D viewpoint is placed at a distance of five times the vertex-center radius of the 24-cell.
Cell-first perspective projection 
In this image, the nearest cell is rendered in red, and the remaining cells are in edge-outline. For clarity, cells facing away from the 4D viewpoint have been culled.
In this image, four of the 8 cells surrounding the nearest cell are shown in green. The fourth cell is behind the central cell in this viewpoint (slightly discernible since the red cell is semi-transparent).
Finally, all 8 cells surrounding the nearest cell are shown, with the last four rendered in magenta.Note that these images do not include cells which are facing away from the 4D viewpoint. Hence, only 9 cells are shown here. On the far side of the 24-cell are another 9 cells in an identical arrangement. The remaining 6 cells lie on the "equator" of the 24-cell, and bridge the two sets of cells.
orthographic projections Coxeter plane F4 Graph 
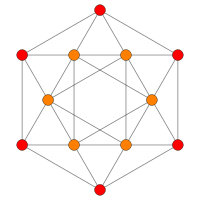
Dihedral symmetry [12] Coxeter plane B3 / A2 (a) B3 / A2 (b) Graph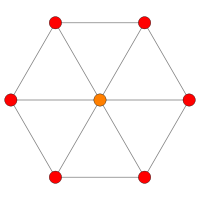 
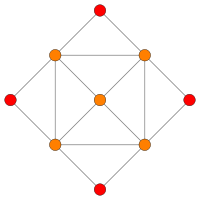
Dihedral symmetry [6] [6] Coxeter plane B4 B2 / A2 Graph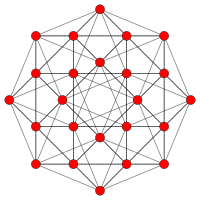 
Dihedral symmetry [8] [4] 
Stereographic projection
Animated cross-section of 24-cell
A 3D projection of a 24-cell performing a simple rotation.
A stereoscopic 3D projection of an icositetrachoron (24-cell).Isometric Orthogonal Projection of:
8 Cell(Tesseract) + 16 Cell = 24 CellThree Coxeter group constructions
There are two lower symmetry forms of the 24-cell, derived as a rectified 16-cell, with B4 or [3,3,4] symmetry drawn bicolored with 8 and 16 octahedral cells. Lastly it can be constructed from D4 or [31,1,1] symmetry, and drawn tricolored with 8 octahedra each.
Three nets of the 24-cell with cells colored by D4, B4, and F4 symmetry Rectified demitesseract Rectified 16-cell Regular 24-cell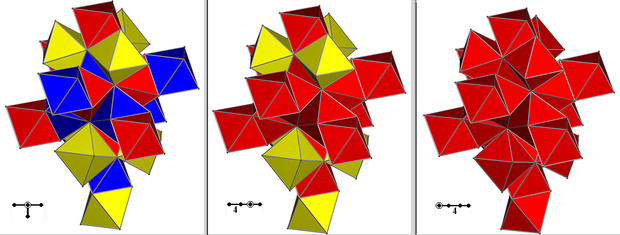 
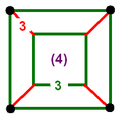
D4: Three sets of 8 rectified tetrahedral cells B4:One set of 16 rectified tetrahedral cells and one set of 8 octahedral cells. F4: One set of 24 octahedral cells Vertex figure
(Each edge corresponds to one triangular face, colored by symmetry arrangement)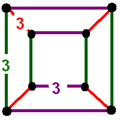
Visualization
The 24-cell consists of 24 octahedral cells. For visualization purposes, it is convenient that the octahedron has opposing parallel faces (a trait it shares with the cells of the tesseract and the 120-cell). One can stack octahedrons face to face in a straight line bent in the 4th direction into a great circle with a circumference of 6 cells. The cell locations lend themselves to a hyperspherical description. Pick an arbitrary cell and label it the "North Pole". Eight great circle meridians (two cells long) radiate out in 3 dimensions, converging at the 3rd "South Pole" cell. This skeleton accounts for 18 of the 24 cells (2 + 8*2). See the table below.
There is another related great circle in the 24-cell, the dual of the one above. A path that traverses 6 vertices solely along edges, resides in the dual of this polytope, which is itself since it is self dual. One can easily follow this path in a rendering of the equatorial cuboctahedron cross-section. One can also follow a great circle route, through the octahedrons' opposing vertices, that is four cells long. This corresponds to traversing diagonally through the squares in the cuboctahedron cross-section. The 24-cell is the only regular polytope in more than two dimensions where you can traverse a great circle purely through opposing vertices (and the interior) of each cell. This great circle is self dual.
Starting at the North Pole, we can build up the 24-cell in 5 latitudinal layers. With the exception of the poles, each layer represents a separate 2-sphere, with the equator being a great 2-sphere. The cells labeled equatorial in the following table are interstitial to the meridian great circle cells. The interstitial "equatorial" cells touch the meridian cells at their faces. They touch each other, and the pole cells at their vertices. This latter subset of eight non-meridian and pole cells has the same relative position to each other as the cells in a tesseract (8-cell), although they touch at their vertices instead of their faces.
Layer # Number of Cells Description Colatitude Region 1 1 cell North Pole 0° Northern Hemisphere 2 8 cells First layer of meridian cells 60° 3 6 cells Non-meridian / interstitial 90° Equator 4 8 cells Second layer of meridian cells 120° Southern Hemisphere 5 1 cell South Pole 180° Total 24 cells The 24-cell can be partitioned into disjoint sets of four of these 6-cell great circle rings, forming a discrete Hopf fibration of four interlocking rings. One ring is "vertical", encompassing the pole cells and four meridian cells. The other three rings each encompass two equatorial cells and four meridian cells, two from the northern hemisphere and two from the southern.
Related 4-polytopes
Several uniform polychora can be derived from the 24-cell via truncation:
- truncating at 1/3 of the edge length yields the truncated 24-cell;
- truncating at 1/2 of the edge length yields the rectified 24-cell;
- and truncating at half the depth to the dual 24-cell yields the bitruncated 24-cell, which is cell-transitive.
The 96 edges of the 24-cell can be partitioned into the golden ratio to produce the 96 vertices of the snub 24-cell. This is done by first placing vectors along the 24-cell's edges such that each two-dimensional face is bounded by a cycle, then similarly partitioning each edge into the golden ratio along the direction of its vector. An analogous modification to an octahedron produces an icosahedron, or "snub octahedron."
Related uniform polytopes
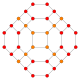
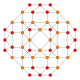
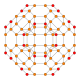
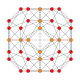
Name 24-cell truncated 24-cell rectified 24-cell cantellated 24-cell bitruncated 24-cell cantitruncated 24-cell runcinated 24-cell runcitruncated 24-cell omnitruncated 24-cell snub 24-cell Schläfli
symbol{3,4,3} t0,1{3,4,3} t1{3,4,3} t0,2{3,4,3} t1,2{3,4,3} t0,1,2{3,4,3} t0,3{3,4,3} t0,1,3{3,4,3} t0,1,2,3{3,4,3} h0,1{3,4,3} Coxeter-Dynkin
diagram
Schlegel
diagram
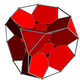
F4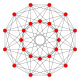 
B4 
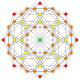
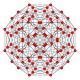
B3(a)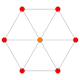 
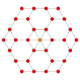
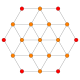
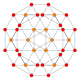
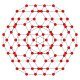
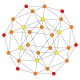
B3(b) 
B2 
The 24-cell can also be derived as a rectified 16-cell:
Name tesseract rectified
tesseracttruncated
tesseractcantellated
tesseractruncinated
tesseractbitruncated
tesseractcantitruncated
tesseractruncitruncated
tesseractomnitruncated
tesseractCoxeter-Dynkin
diagramSchläfli
symbol{4,3,3} t1{4,3,3} t0,1{4,3,3} t0,2{4,3,3} t0,3{4,3,3} t1,2{4,3,3} t0,1,2{4,3,3} t0,1,3{4,3,3} t0,1,2,3{4,3,3} Schlegel
diagram
B4 Coxeter plane graph 
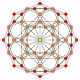
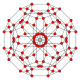
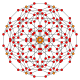
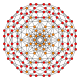
Name 16-cell rectified
16-celltruncated
16-cellcantellated
16-cellruncinated
16-cellbitruncated
16-cellcantitruncated
16-cellruncitruncated
16-cellomnitruncated
16-cellCoxeter-Dynkin
diagramSchläfli
symbol{3,3,4} t1{3,3,4} t0,1{3,3,4} t0,2{3,3,4} t0,3{3,3,4} t1,2{3,3,4} t0,1,2{3,3,4} t0,1,3{3,3,4} t0,1,2,3{3,3,4} Schlegel
diagram
B4 Coxeter plane graph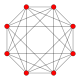 
See also
References
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- Weisstein, Eric W., "24-Cell" from MathWorld. (also under Icositetrachoron)
- Richard Klitzing, 4D uniform polytopes (polychora), x3o4o3o - ico
- Olshevsky, George, Icositetrachoron at Glossary for Hyperspace.
- Der 24-Zeller (24-cell) Marco Möller's Regular polytopes in R4 (German)
External links
- 24-cell animations
- 24-cell in stereographic projections
- 24-cell description and diagrams
- Petrie dodecagons in the 24-cell: mathematics and animation software
Fundamental convex regular and uniform polytopes in dimensions 2–10 Family An BCn Dn E6 / E7 / E8 / F4 / G2 Hn Regular polygon Triangle Square Hexagon Pentagon Uniform polyhedron Tetrahedron Octahedron • Cube Demicube Dodecahedron • Icosahedron Uniform polychoron 5-cell 16-cell • Tesseract Demitesseract 24-cell 120-cell • 600-cell Uniform 5-polytope 5-simplex 5-orthoplex • 5-cube 5-demicube Uniform 6-polytope 6-simplex 6-orthoplex • 6-cube 6-demicube 122 • 221 Uniform 7-polytope 7-simplex 7-orthoplex • 7-cube 7-demicube 132 • 231 • 321 Uniform 8-polytope 8-simplex 8-orthoplex • 8-cube 8-demicube 142 • 241 • 421 Uniform 9-polytope 9-simplex 9-orthoplex • 9-cube 9-demicube Uniform 10-polytope 10-simplex 10-orthoplex • 10-cube 10-demicube n-polytopes n-simplex n-orthoplex • n-cube n-demicube 1k2 • 2k1 • k21 pentagonal polytope Topics: Polytope families • Regular polytope • List of regular polytopes Categories:- Four-dimensional geometry
- Polychora
Wikimedia Foundation. 2010.
