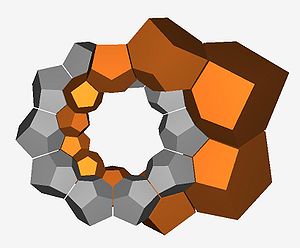
120-cell

120-cell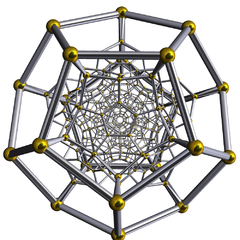
Schlegel diagram (vertices and edges)
Type	Convex regular 4-polytope
Schläfli symbol	{5,3,3}
Coxeter-Dynkin diagram
Cells	120 {5,3}
Faces	720 {5}
Edges	1200
Vertices	600
Vertex figure	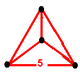tetrahedron
Petrie polygon	30-gon
Coxeter group	H4, [3,3,5]
Dual	600-cell
Properties	convex, isogonal, isotoxal, isohedral
Uniform index	32

In geometry, the 120-cell (or hecatonicosachoron) is the convex regular 4-polytope with Schläfli symbol {5,3,3}.

The boundary of the 120-cell is composed of 120 dodecahedral cells with 4 meeting at each vertex.

It can be thought of as the 4-dimensional analog of the dodecahedron and has been called a dodecaplex (short for "dodecahedral complex"), hyperdodecahedron, and polydodecahedron. Just as a dodecahedron can be built up as a model with 12 pentagons, 3 around each vertex, the dodecaplex can be built up from 120 dodecahedrons, with 3 around each edge.

The Davis 120-cell, introduced by Davis (1985), is a compact 4-dimensional hyperbolic manifold obtained by identifying opposite faces of the 120-cell, whose universal cover gives the regular honeycomb {5,3,3,5} of 4-dimensional hyperbolic space.

Elements

• There are 120 cells, 720 pentagonal faces, 1200 edges, and 600 vertices.
• There are 4 dodecahedra, 6 pentagons, and 4 edges meeting at every vertex.
• There are 3 dodecahedra and 3 pentagons meeting every edge.

• The dual polytope of the 120-cell is the 600-cell.
• The vertex figure of the 120-cell is a tetrahedron.

Cartesian coordinates

The 600 vertices of the 120-cell include all permutations of:^[1]

(0, 0, ±2, ±2)

(±1, ±1, ±1, ±√5)

(±φ^-2, ±φ, ±φ, ±φ)

(±φ^-1, ±φ^-1, ±φ^-1, ±φ²)

and all even permutations of

(0, ±φ^-2, ±1, ±φ²)

(0, ±φ^-1, ±φ, ±√5)

(±φ^-1, ±1, ±φ, ±2)

where φ (also called τ) is the golden ratio, (1+√5)/2.

Visualization

The 120-cell consists of 120 dodecahedral cells. For visualization purposes, it is convenient that the dodecahedron has opposing parallel faces (a trait it shares with the cells of the tesseract and the 24-cell). One can stack dodecahedrons face to face in a straight line bent in the 4th direction into a great circle with a circumference of 10 cells. Starting from this initial ten cell construct there are two common visualizations one can use: a layered stereographic projection, and a structure of intertwining rings.

Layered stereographic projection

The cell locations lend themselves to a hyperspherical description. Pick an arbitrary cell and label it the "North Pole". Twelve great circle meridians (four cells long) radiate out in 3 dimensions, converging at the 5th "South Pole" cell. This skeleton accounts for 50 of the 120 cells (2 + 4*12).

Starting at the North Pole, we can build up the 120-cell in 9 latitudinal layers, with allusions to terrestrial 2-sphere topography in the table below. With the exception of the poles, each layer represents a separate 2-sphere, with the equator being a great 2-sphere. The centroids of the 30 equatorial cells form the vertices of an icosidodecahedron, with the meridians (as described above) passing through the center of each pentagonal face. The cells labeled "interstitial" in the following table do not fall on meridian great circles.

Layer #	Number of Cells	Description	Colatitude	Region
1	1 cell	North Pole	0°	Northern Hemisphere
2	12 cells	First layer of meridian cells	36°
3	20 cells	Non-meridian / interstitial / "Tropic of Cancer"	60°
4	12 cells	Second layer of meridian cells	72°
5	30 cells	Non-meridian / interstitial	90°	Equator
6	12 cells	Third layer of meridian cells	108°	Southern Hemisphere
7	20 cells	Non-meridian / interstitial / "Tropic of Capricorn"	120°
8	12 cells	Fourth layer of meridian cells	144°
9	1 cell	South Pole	180°
Total	120 cells

Layers 3 and 7's cells are located directly over the pole cell's vertices. Layer 5's cells are located over the pole cell's edges.

Intertwining rings

Two intertwining rings of the 120-cell.

The 120-cell can be partitioned into 12 disjoint 10-cell great circle rings, forming a discrete/quantized Hopf fibration. Starting with one 10-cell ring, one can place another ring along side it that spirals around the original ring one complete revolution in ten cells. Five such 10-cell rings can be placed adjacent to the original 10-cell ring. Although the outer rings "spiral" around the inner ring (and each other), they actually have no helical torsion. They are all equivalent. The spiraling is a result of the 3-sphere curvature. The inner ring and the five outer rings now form a six ring, 60-cell solid torus. One can continue adding 10-cell rings adjacent to the previous ones, but it's more instructive to construct a second torus, disjoint from the one above, from the remaining 60 cells, that interlocks with the first. The 120-cell, like the 3-sphere, is the union of these two (Clifford) tori. If the center ring of the first torus is a meridian great circle as defined above, the center ring of the second torus is the equatorial great circle that is centered on the meridian circle. Also note that the spiraling shell of 50 cells around a center ring can be either left handed or right handed. It's just a matter of partitioning the cells in the shell differently, i.e. picking another set of disjoint great circles.

Other great circle constructs

There is another great circle path of interest that alternately passes through opposing cell vertices, then along an edge. This path consists of 6 cells and 6 edges. Both the above great circle paths have dual great circle paths in the 600-cell. The 10 cell face to face path above maps to a 10 vertices path solely traversing along edges in the 600-cell, forming a decagon. The alternating cell/edge path above maps to a path consisting of 12 tetrahedrons alternately meeting face to face then vertex to vertex in the 600-cell.

Projections

Orthogonal projections

Orthogonal projections of the 120-cell can be done in 2D by defining two orthonormal basis vectors for a specific view direction.

Orthographic projections by Coxeter planes

H4	-	F4
[30]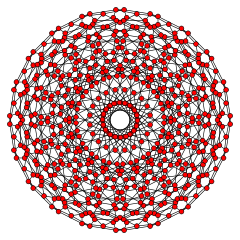	[20]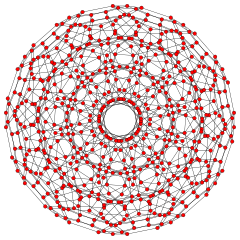	[12]
H3	A2 / B3 / D4	A3 / B2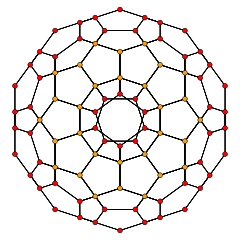
[10]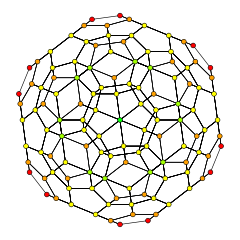	[6]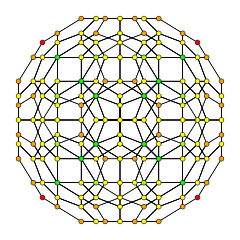	[4]

3-dimensional orthogonal projections can also be made with three orthonormal basis vectors, and displayed as a 3d model, and then projecting a certain perspective in 3D for a 2d image.

3D orthographic projections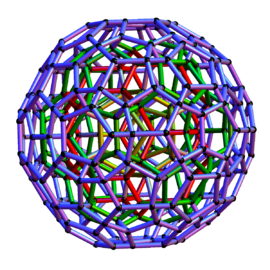

3D isometric projection

Animated 4D rotation

Perspective projections

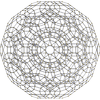
These projections use perspective projection, from a specific view point in 4-dimensions, and projecting the model as a 3D shadow. Therefore faces and cells that look larger are merely closer to the 4D viewpoint. Schlegel diagrams use perspective to show 4 dimensional figures, choosing a point above a specific cell, thus making the cell as the envelope of the 3D model, and other cells are smaller seen inside it. Stereographic projection use the same approach, but are shown with curved edges, representing the polytope a tiling of a 3-sphere.

A comparison of perspective projections from 3D to 2D is shown in anology.

Comparison with regular dodecahedron

Projection	Dodecahedron	Dodecaplex
Schlegel diagram	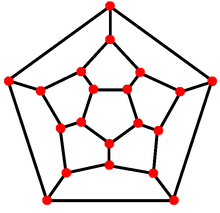12 pentagon faces in the plane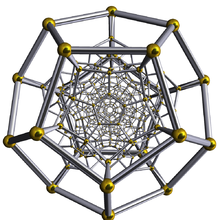	120 dodecahedral cells in 3-space
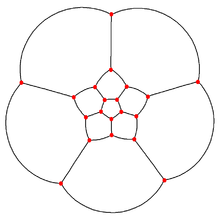
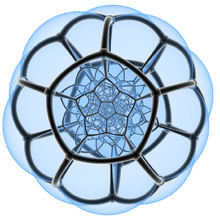
Stereographic projection		With transparent faces

Perspective projection
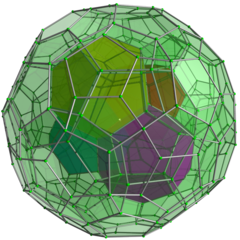
	Cell-first perspective projection at 5 times the distance from the center to a vertex, with these enhancements applied: Nearest dodecahedron to the 4D viewpoint rendered in yellow The 12 dodecahedra immediately adjoining it rendered in cyan; The remaining dodecahedra rendered in green; Cells facing away from the 4D viewpoint (those lying on the "far side" of the 120-cell) culled to minimize clutter in the final image.
	Vertex-first perspective projection at 5 times the distance from center to a vertex, with these enhancements: Four cells surrounding nearest vertex shown in 4 colors Nearest vertex shown in white (center of image where 4 cells meet) Remaining cells shown in transparent green Cells facing away from 4D viewpoint culled for clarity
	A 3D projection of a 120-cell performing a simple rotation.
	A 3D projection of a 120-cell performing a simple rotation (from the inside).
	Animated 4D rotation

See also

• Uniform polychora family with [5,3,3] symmetry
• 57-cell – an abstract regular polychoron constructed from 57 hemi-dodecahedra.

Notes

1. ^ Weisstein, Eric W., "120-cell" from MathWorld.

References

• H. S. M. Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8.
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  • (Paper 22) H.S.M. Coxeter, Regular and Semi-Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
• Davis, Michael W. (1985), "A hyperbolic 4-manifold", Proceedings of the American Mathematical Society 93 (2): 325–328, doi:10.2307/2044771, ISSN 0002-9939, MR770546 
• N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
• Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation [2]

External links

• Weisstein, Eric W., "120-Cell" from MathWorld.
• Olshevsky, George, Hecatonicosachoron at Glossary for Hyperspace.
  • Convex uniform polychora based on the hecatonicosachoron (120-cell) and hexacosichoron (600-cell) - Model 32, George Olshevsky.
• Richard Klitzing, 4D uniform polytopes (polychora), o3o3o5x - hi
• Der 600-Zeller (600-cell) Marco Möller's Regular polytopes in R⁴ (German)
• 120-cell explorer – A free interactive program that allows you to learn about a number of the 120-cell symmetries. The 120-cell is projected to 3 dimensions and then rendered using OpenGL.
• Construction of the Hyper-Dodecahedron
• YouTube animation of the construction of the 120-cell Gian Marco Todesco.

H₄ family polytopes by name, Coxeter-Dynkin diagram, and Schläfli symbol

120-cell	rectified 120-cell	truncated 120-cell	cantellated 120-cell	runcinated 120-cell	bitruncated 120-cell	cantitruncated 120-cell	runcitruncated 120-cell	omnitruncated 120-cell
{5,3,3}	t1{5,3,3}	t0,1{5,3,3}	t0,2{5,3,3}	t0,3{5,3,3}	t1,2{5,3,3}	t0,1,2{5,3,3}	t0,1,3{5,3,3}	t0,1,2,3{5,3,3}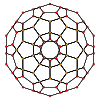
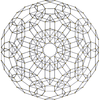
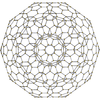
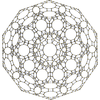
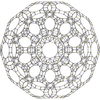
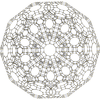
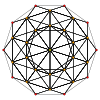
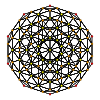
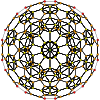
600-cell	rectified 600-cell	truncated 600-cell	cantellated 600-cell	runcinated 600-cell	bitruncated 600-cell	cantitruncated 600-cell	runcitruncated 600-cell	omnitruncated 600-cell
{3,3,5}	t1{3,3,5}	t0,1{3,3,5}	t0,2{3,3,5}	t0,3{3,3,5}	t1,2{3,3,5}	t0,1,2{3,3,5}	t0,1,3{3,3,5}	t0,1,2,3{3,3,5}