- Rectified 600-cell
-
Four rectifications 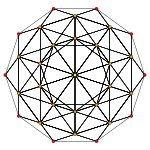
600-cell







Rectified 600-cell







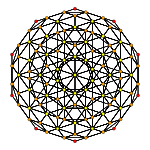
Rectified 120-cell







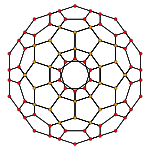
120-cell







Orthogonal projections in H3 Coxeter plane In geometry, a rectified 600-cell is a uniform polychoron (4-dimensional uniform polytope) formed as the rectification of the regular 600-cell.
There are four rectifications of the 600-cell, including the zeroth, the 600-cell itself. Tbe birectified 600-cell is more easily seen as a rectified 120-cell, and the trirectified 600-cell is the same as the dual 120-cell.
Contents
Rectified 600-cell
Rectified 600-cell 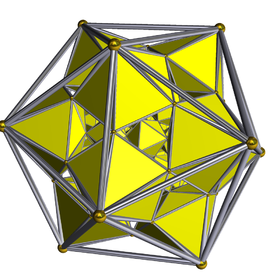
Schlegel diagram, shown as Birectified 120-cell, with 119 icosahedral cells coloredType Uniform polychoron Uniform index 34 Schläfli symbol t1{3,3,5} Coxeter-Dynkin diagram 






Cells 600 (3.3.3.3) 
120 {3,5}
Faces 1200+2400 {3} Edges 3600 Vertices 720 Vertex figure 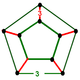
pentagonal prismSymmetry group H4 or [3,3,5] Properties convex, edge-transitive In geometry, the rectified 600-cell is a convex uniform polychoron composed of 600 regular octahedra and 120 icosahedra cells. Each edge has two octahedra and one icosahedron. Each vertex has five octahedra and two icosahedra. In total it has 3600 triangle faces, 3600 edges, and 720 vertices.
It is one of three semiregular polychora made of two or more cells which are platonic solids, discovered by Thorold Gosset in his 1900 paper. He called it a octicosahedric for being made of octahedron and icosahedron cells.
Containing the cell realms of both the regular 120-cell and the regular 600-cell, it can be considered analogous to the polyhedron icosidodecahedron, which is a rectified icosahedron and rectified dodecahedron.
The vertex figure of the rectified 600-cell is a uniform pentagonal prism.
Alternate names
- Icosahedral hexacosihecatonicosachoron
- Rectified 600-cell (Norman W. Johnson)
- Rectified hexacosichoron
- Rectified polytetrahedron
- Rox (Jonathan Bowers)
Images
Orthographic projections by Coxeter planes H4 - F4 
[30]
[20]
[12]H3 A2 / B3 / D4 A3 / B2 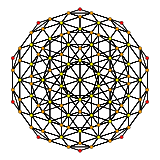
[10]
[6]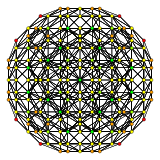
[4]Stereographic projection 
Related polytopes
H4 family polytopes by name, Coxeter-Dynkin diagram, and Schläfli symbol 120-cell rectified
120-celltruncated
120-cellcantellated
120-cellruncinated
120-cellbitruncated
120-cellcantitruncated
120-cellruncitruncated
120-cellomnitruncated
120-cell






























































{5,3,3} t1{5,3,3} t0,1{5,3,3} t0,2{5,3,3} t0,3{5,3,3} t1,2{5,3,3} t0,1,2{5,3,3} t0,1,3{5,3,3} t0,1,2,3{5,3,3} 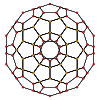



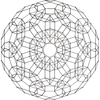
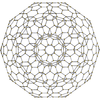



600-cell rectified
600-celltruncated
600-cellcantellated
600-cellruncinated
600-cellbitruncated
600-cellcantitruncated
600-cellruncitruncated
600-cellomnitruncated
600-cell






























































{3,3,5} t1{3,3,5} t0,1{3,3,5} t0,2{3,3,5} t0,3{3,3,5} t1,2{3,3,5} t0,1,2{3,3,5} t0,1,3{3,3,5} t0,1,2,3{3,3,5} References
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi-Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation [2]
External links
- Convex uniform polychora based on the hecatonicosachoron (120-cell) and hexacosichoron (600-cell) - Model 34, George Olshevsky.
- Richard Klitzing, 4D uniform polytopes (polychora), o3x3o5o - rox
- Archimedisches Polychor Nr. 45 (rectified 600-cell) Marco Möller's Archimedean polytopes in R4 (German)
Fundamental convex regular and uniform polytopes in dimensions 2–10 Family An BCn Dn E6 / E7 / E8 / F4 / G2 Hn Regular polygon Triangle Square Hexagon Pentagon Uniform polyhedron Tetrahedron Octahedron • Cube Demicube Dodecahedron • Icosahedron Uniform polychoron 5-cell 16-cell • Tesseract Demitesseract 24-cell 120-cell • 600-cell Uniform 5-polytope 5-simplex 5-orthoplex • 5-cube 5-demicube Uniform 6-polytope 6-simplex 6-orthoplex • 6-cube 6-demicube 122 • 221 Uniform 7-polytope 7-simplex 7-orthoplex • 7-cube 7-demicube 132 • 231 • 321 Uniform 8-polytope 8-simplex 8-orthoplex • 8-cube 8-demicube 142 • 241 • 421 Uniform 9-polytope 9-simplex 9-orthoplex • 9-cube 9-demicube Uniform 10-polytope 10-simplex 10-orthoplex • 10-cube 10-demicube n-polytopes n-simplex n-orthoplex • n-cube n-demicube 1k2 • 2k1 • k21 pentagonal polytope Topics: Polytope families • Regular polytope • List of regular polytopes Categories:- Four-dimensional geometry
- Polychora
Wikimedia Foundation. 2010.