- 10-demicube
-
Demidekeract
(10-demicube)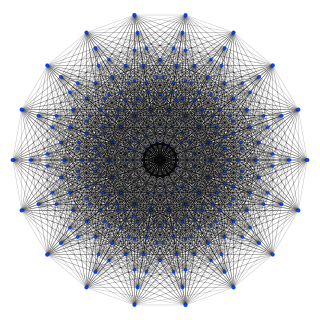
Petrie polygon projectionType Uniform 10-polytope Family demihypercube Coxeter symbol 171 Schläfli symbol {31,7,1}
h{4,3,3,3,3,3,3,3,3}
s{2,2,2,2,2,2,2,2,2}Coxeter-Dynkin diagram 






















































9-faces 532 20 {31,6,1} 
512 {38}
8-faces 5300 180 {31,5,1} 
5120 {37}
7-faces 24000 960 {31,4,1} 
23040 {36}
6-faces 64800 3360 {31,3,1} 
61440 {35}
5-faces 115584 8064 {31,2,1} 
107520 {34}
4-faces 142464 13440 {31,1,1} 
129024 {33}
Cells 122880 15360 {31,0,1} 
107520 {3,3}
Faces 61440 {3} 
Edges 11520 Vertices 512 Vertex figure Rectified 9-simplex

Symmetry group D10, [37,1,1] = [1+,4,38]
[29]+Dual ? Properties convex In geometry, a demidekeract or 10-demicube is a uniform 10-polytope, constructed from the 10-cube with alternated vertices deleted. It is part of a dimensionally infinite family of uniform polytopes called demihypercubes.
Coxeter named this polytope as 171 from its Coxeter-Dynkin diagram, with a ring on one of the 1-length Coxeter-Dynkin diagram branches.
Contents
Cartesian coordinates
Cartesian coordinates for the vertices of a demidekeract centered at the origin are alternate halves of the dekeract:
- (±1,±1,±1,±1,±1,±1,±1,±1,±1,±1)
with an odd number of plus signs.
Images
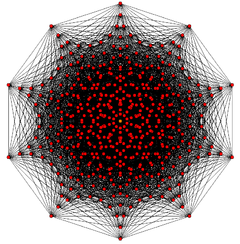
B10 coxeter plane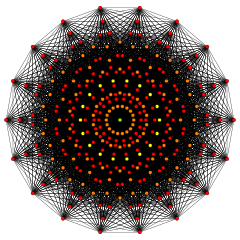
D10 coxeter plane
(Vertices are colored by multiplicity: red, orange, yellow, green = 1,2,4,8)References
- H.S.M. Coxeter:
- Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1n1)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- Richard Klitzing, 10D uniform polytopes (polyxenna), x3o3o *b3o3o3o3o3o3o3o - hede
External links
- Olshevsky, George, Demienneract at Glossary for Hyperspace.
- Multi-dimensional Glossary
Fundamental convex regular and uniform polytopes in dimensions 2–10 Family An BCn Dn E6 / E7 / E8 / F4 / G2 Hn Regular polygon Triangle Square Hexagon Pentagon Uniform polyhedron Tetrahedron Octahedron • Cube Demicube Dodecahedron • Icosahedron Uniform polychoron 5-cell 16-cell • Tesseract Demitesseract 24-cell 120-cell • 600-cell Uniform 5-polytope 5-simplex 5-orthoplex • 5-cube 5-demicube Uniform 6-polytope 6-simplex 6-orthoplex • 6-cube 6-demicube 122 • 221 Uniform 7-polytope 7-simplex 7-orthoplex • 7-cube 7-demicube 132 • 231 • 321 Uniform 8-polytope 8-simplex 8-orthoplex • 8-cube 8-demicube 142 • 241 • 421 Uniform 9-polytope 9-simplex 9-orthoplex • 9-cube 9-demicube Uniform 10-polytope 10-simplex 10-orthoplex • 10-cube 10-demicube n-polytopes n-simplex n-orthoplex • n-cube n-demicube 1k2 • 2k1 • k21 pentagonal polytope Topics: Polytope families • Regular polytope • List of regular polytopes Categories:- 10-polytopes
Wikimedia Foundation. 2010.
