16-cell

Regular hexadecachoron (16-cell) (4-orthoplex)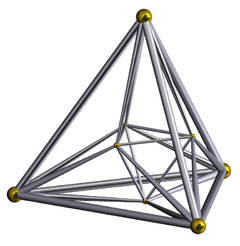
Schlegel diagram (vertices and edges)
Type	Convex regular 4-polytope
Schläfli symbol	{3,3,4} {3,31,1} h{4,3,3} s{2,2,2}
Coxeter-Dynkin diagram
Cells	16 {3,3}
Faces	32 {3}
Edges	24
Vertices	8
Vertex figure	Octahedron
Petrie polygon	octagon
Coxeter group	C4, [3,3,4] D4, [31,1,1] [23] (half)
Symmetry group	[3,3,4], order 384 [31,1,1], order 192 [3,4,2+], order 48 [23]+, order 8
Dual	Tesseract
Properties	convex, isogonal, isotoxal, isohedral
Uniform index	12

In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.

It is a part of an infinite family of polytopes, called cross-polytopes or orthoplexes. The dual polytope is the tesseract (4-cube). Conway's name for a cross-polytope is orthoplex, for orthant complex.

Geometry

It is bounded by 16 cells, all of which are regular tetrahedra. It has 32 triangular faces, 24 edges, and 8 vertices. The 24 edges bound 6 squares lying in the 6 coordinate planes.

The eight vertices of the 16-cell are (±1, 0, 0, 0), (0, ±1, 0, 0), (0, 0, ±1, 0), (0, 0, 0, ±1). All vertices are connected by edges except opposite pairs.

The Schläfli symbol of the 16-cell is {3,3,4}. Its vertex figure is a regular octahedron. There are 8 tetrahedra, 12 triangles, and 6 edges meeting at every vertex. Its edge figure is a square. There are 4 tetrahedra and 4 triangles meeting at every edge.

There is a lower symmetry form of the 16-cell, called a demitesseract or 4-demicube, a member of the demihypercube family, and represented by h{4,3,3}, and Coxeter diagrams or . It can be drawn bicolored with alternating tetrahedral cells.

It can also be seen in lower symmetry form as a tetrahedral antiprism, constructed by 2 parallel tetrahedra in dual configurations, connected by 8 (possibly elongated) tetrahedra. It is represented by h_0,1{2,4,3}, and Coxeter diagram: .

It can also be seen as a snub 4-orthotope, represented by s{2,2,2}, and Coxeter diagram: .

Images

Stereographic projection	A 3D projection of a 16-cell performing a simple rotation.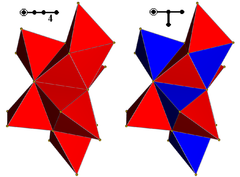
The 16-cell has two Wythoff constructions, a regular form and alternated form, shown here as nets, the second being represented by alternately two colors of tetrahedral cells.

orthographic projections

Coxeter plane	B4	B3 / D4 / A2	B2 / D3
Graph
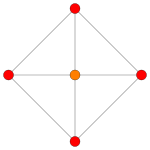
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	F4	A3
Graph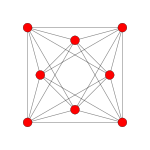
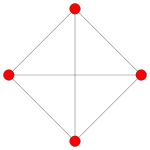
Dihedral symmetry	[12/3]	[4]

Orthogonal projection graphs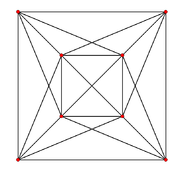

demitesseract in order-4 Petrie polygon symmetry as an alternated tesseract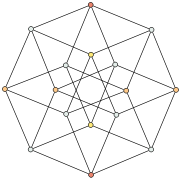

Tesseract

Tessellations

One can tessellate 4-dimensional Euclidean space by regular 16-cells. This is called the hexadecachoric honeycomb and has Schläfli symbol {3,3,4,3}. The dual tessellation, icositetrachoric honeycomb, {3,4,3,3}, is made of by regular 24-cells. Together with the tesseractic honeycomb {4,3,3,4}, these are the only three regular tessellations of R⁴. Each 16-cell has 16 neighbors with which it shares an octahedron, 24 neighbors with which it shares only an edge, and 72 neighbors with which it shares only a single point. Twenty-four 16-cells meet at any given vertex in this tessellation.

Projections

Projection envelopes of the 16-cell. (Each cell is drawn with different color faces, inverted cells are undrawn)

The cell-first parallel projection of the 16-cell into 3-space has a cubical envelope. The closest and farthest cells are projected to inscribed tetrahedra within the cube, corresponding with the two possible ways to inscribe a regular tetrahedron in a cube. Surrounding each of these tetrahedra are 4 other (non-regular) tetrahedral volumes that are the images of the 4 surrounding tetrahedral cells, filling up the space between the inscribed tetrahedron and the cube. The remaining 6 cells are projected onto the square faces of the cube. In this projection of the 16-cell, all its edges lie on the faces of the cubical envelope.

The cell-first perspective projection of the 16-cell into 3-space has a triakis tetrahedral envelope. The layout of the cells within this envelope are analogous to that of the cell-first parallel projection.

The vertex-first parallel projection of the 16-cell into 3-space has an octahedral envelope. This octahedron can be divided into 8 tetrahedral volumes, by cutting along the coordinate planes. Each of these volumes is the image of a pair of cells in the 16-cell. The closest vertex of the 16-cell to the viewer projects onto the center of the octahedron.

Finally the edge-first parallel projection has a shortened octahedral envelope, and the face-first parallel projection has a hexagonal bipyramidal envelope.

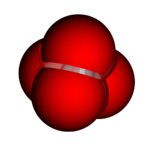
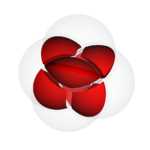
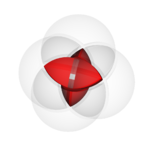
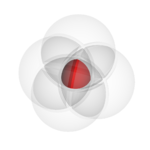
4 sphere Venn Diagram

The usual projection of the 16-cell and 4 intersecting spheres (a Venn diagram of 4 sets) form topologically the same object in 3D-space:

Related uniform polytopes

Name	tesseract	rectified tesseract	truncated tesseract	cantellated tesseract	runcinated tesseract	bitruncated tesseract	cantitruncated tesseract	runcitruncated tesseract	omnitruncated tesseract
Coxeter-Dynkin diagram
Schläfli symbol	{4,3,3}	t1{4,3,3}	t0,1{4,3,3}	t0,2{4,3,3}	t0,3{4,3,3}	t1,2{4,3,3}	t0,1,2{4,3,3}	t0,1,3{4,3,3}	t0,1,2,3{4,3,3}
Schlegel diagram
B4 Coxeter plane graph
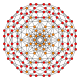
Name	16-cell	rectified 16-cell	truncated 16-cell	cantellated 16-cell	runcinated 16-cell	bitruncated 16-cell	cantitruncated 16-cell	runcitruncated 16-cell	omnitruncated 16-cell
Coxeter-Dynkin diagram
Schläfli symbol	{3,3,4}	t1{3,3,4}	t0,1{3,3,4}	t0,2{3,3,4}	t0,3{3,3,4}	t1,2{3,3,4}	t0,1,2{3,3,4}	t0,1,3{3,3,4}	t0,1,2,3{3,3,4}
Schlegel diagram
B4 Coxeter plane graph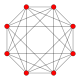

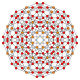
See also

• 24-cell
• Polychoron

References

• T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
• H.S.M. Coxeter:
  • Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1_n1)
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)

External links

• Weisstein, Eric W., "16-Cell" from MathWorld.
• Olshevsky, George, Hexadecachoron at Glossary for Hyperspace.
  • 2. Convex uniform polychora based on the tesseract (8-cell) and hexadecachoron (16-cell) - Model 12, George Olshevsky.
• Der 16-Zeller (16-cell) Marco Möller's Regular polytopes in R⁴ (German)
• Description and diagrams of 16-cell projections
• Richard Klitzing, 4D uniform polytopes (polychora), x3o3o4o - hex