- Cross-polytope
-
In geometry, a cross-polytope,[1] orthoplex,[2] hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of (±1, 0, 0, …, 0). The cross-polytope is the convex hull of its vertices. Its facets are simplexes of the previous dimension, while the cross-polytope's vertex figure is another cross-polytope from the previous dimension.
The n-dimensional cross-polytope can also be defined as the closed unit ball (or, according to some authors, its boundary) in the ℓ1-norm on Rn:
In 1 dimension the cross-polytope is simply the line segment [−1, +1], in 2 dimensions it is a square (or diamond) with vertices {(±1, 0), (0, ±1)}. In 3 dimensions it is an octahedron—one of the five convex regular polyhedra known as the Platonic solids. Higher-dimensional cross-polytopes are generalizations of these.
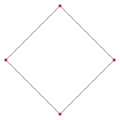


2 dimensions
square3 dimensions
octahedron4 dimensions
16-cellThe cross-polytope is the dual polytope of the hypercube. The 1-skeleton of a n-dimensional cross-polytope is a Turán graph T(2n,n).
Contents
4 dimensions
The 4-dimensional cross-polytope also goes by the name hexadecachoron or 16-cell. It is one of six convex regular 4-polytopes. These polychora were first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.
Higher dimensions
The cross polytope family is one of three regular polytope families, labeled by Coxeter as βn, the other two being the hypercube family, labeled as γn, and the simplices, labeled as αn. A fourth family, the infinite tessellations of hypercubes, he labeled as δn.
The n-dimensional cross-polytope has 2n vertices, and 2n facets (n−1 dimensional components) all of which are n−1 simplices. The vertex figures are all n − 1 cross-polytopes. The Schläfli symbol of the cross-polytope is {3,3,…,3,4}.
The number of k-dimensional components (vertices, edges, faces, …, facets) in an n-dimensional cross-polytope is given by (see binomial coefficient):
The volume of the n-dimensional cross-polytope is
There are many possible orthographic projections that can show the cross-polytopes as 2-dimensional graphs. Petrie polygon projections map the points into a regular 2n-gon or lower order regular polygons. A second projection takes the 2(n-1)-gon petrie polygon of the lower dimension, seen as a bipyramid, projected down the axis, with 2 vertices mapped into the center.
Cross-polytope elements n βn
k11Name(s)
GraphGraph
2n-gonGraph
2(n-1)-gonSchläfli Coxeter-Dynkin
diagramsVertices Edges Faces Cells 4-faces 5-faces 6-faces 7-faces 8-faces 9-faces 1 β1 Line segment
1-orthoplex
{} 
2 2 β2
−111Bicross
square
2-orthoplex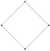
{4}
{} x {}





4 4 3 β3
011Tricross
octahedron
3-orthoplex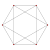

{3,4}
{30,1,1}







6 12 8 4 β4
111Tetracross
16-cell
4-orthoplex

{3,3,4}
{31,1,1}











8 24 32 16 5 β5
211Pentacross
5-orthoplex

{33,4}
{32,1,1}















10 40 80 80 32 6 β6
311Hexacross
6-orthoplex

{34,4}
{33,1,1}



















12 60 160 240 192 64 7 β7
411Heptacross
7-orthoplex

{35,4}
{34,1,1}























14 84 280 560 672 448 128 8 β8
511Octacross
8-orthoplex

{36,4}
{35,1,1}



























16 112 448 1120 1792 1792 1024 256 9 β9
611Enneacross
9-orthoplex

{37,4}
{36,1,1}































18 144 672 2016 4032 5376 4608 2304 512 10 β10
711Decacross
10-orthoplex

{38,4}
{37,1,1}



































20 180 960 3360 8064 13440 15360 11520 5120 1024 ... n βn
k11n-cross
n-orthoplex{3n − 2,4}
{3n − 3,1,1}



 ...
...








 ...
...




2n 0-faces, ...  k-faces ..., 2n (n-1)-faces
k-faces ..., 2n (n-1)-facesThe vertices of an axis-aligned cross polytope are all at equal distance from each other in the Manhattan distance (L1 norm). Kusner's conjecture states that this set of 2d points is the largest possible equidistant set for this distance.[3]
See also
- List of regular polytopes
- Hyperoctahedral group, the symmetry group of the cross-polytope
Notes
- ^ Elte, E. L. (1912), The Semiregular Polytopes of the Hyperspaces, Groningen: University of Groningen Chapter IV, five dimensional semiregular polytope [1]
- ^ Conway calls it an n-orthoplex for orthant complex.
- ^ Guy, Richard K. (1983), "An olla-podrida of open problems, often oddly posed", American Mathematical Monthly 90 (3): 196–200, http://www.jstor.org/stable/2975549.
References
- Coxeter, H. S. M. (1973). Regular Polytopes (3rd ed. ed.). New York: Dover Publications. pp. 121–122. ISBN 0-486-61480-8. p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n>=5)
External links
- Weisstein, Eric W., "Cross polytope" from MathWorld.
- Polytope Viewer[dead link] (Click <polytopes...> to select cross polytope.)
- Olshevsky, George, Cross polytope at Glossary for Hyperspace.
Dimension Dimensional spaces One · Two · Three · Four · Five · Six · Seven · Eight · n-dimensions · Spacetime · Projective space · Hyperplane
Polytopes and Shapes Concepts and mathematics Cartesian coordinates · Linear algebra · Geometric algebra · Conformal geometry · Reflection · Rotation · Plane of rotation · Space · Fractal dimension · MultiverseCategory Fundamental convex regular and uniform polytopes in dimensions 2–10 Family An BCn Dn E6 / E7 / E8 / F4 / G2 Hn Regular polygon Triangle Square Hexagon Pentagon Uniform polyhedron Tetrahedron Octahedron • Cube Demicube Dodecahedron • Icosahedron Uniform polychoron 5-cell 16-cell • Tesseract Demitesseract 24-cell 120-cell • 600-cell Uniform 5-polytope 5-simplex 5-orthoplex • 5-cube 5-demicube Uniform 6-polytope 6-simplex 6-orthoplex • 6-cube 6-demicube 122 • 221 Uniform 7-polytope 7-simplex 7-orthoplex • 7-cube 7-demicube 132 • 231 • 321 Uniform 8-polytope 8-simplex 8-orthoplex • 8-cube 8-demicube 142 • 241 • 421 Uniform 9-polytope 9-simplex 9-orthoplex • 9-cube 9-demicube Uniform 10-polytope 10-simplex 10-orthoplex • 10-cube 10-demicube n-polytopes n-simplex n-orthoplex • n-cube n-demicube 1k2 • 2k1 • k21 pentagonal polytope Topics: Polytope families • Regular polytope • List of regular polytopes Categories:- Polytopes
- Four-dimensional geometry
Wikimedia Foundation. 2010.



