Hyperrectangle

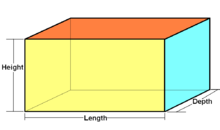A rectangular cuboid is a 3-orthotope

In geometry, an orthotope^[1] (also called a hyperrectangle or a box) is the generalization of a rectangle for higher dimensions, formally defined as the Cartesian product of intervals.

A three-dimensional orthotope is also called a right rectangular prism, rectangular cuboid, or rectangular parallelepiped.

A special case of an n-orthotope, where all edges are equal length, is the n-hypercube.^[1]

By analogy, the term "hyperrectangle" or "box" refers to Cartesian products of orthogonal intervals of other kinds, such as ranges of keys in database theory or ranges of integers, rather than real numbers.^{[citation needed]}

See also

• Bounding box

Notes

1. ^ ^{a b} Coxeter, 1973

References

• Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, pp. 122-123, 1973.

External links

• Weisstein, Eric W., "Rectangular parallelepiped" from MathWorld.
• Weisstein, Eric W., "Orthotope" from MathWorld.

This geometry-related article is a stub. You can help Wikipedia by expanding it.v · Categories: Polytopes Prismatoid polyhedra Geometry stubs Wikimedia Foundation. 2010. Игры ⚽ Поможем сделать НИР Childebert III Dunelm Look at other dictionaries: Implicit kd-tree — An implicit k d tree is a k d tree defined implicitly above a rectilinear grid. Its splitting planes positions and orientations are not given explicitly but implicitly by some recursive splitting function defined on the hyperrectangles belonging… …   Wikipedia Hypercube — This article is about the mathematical concept. For the film, see Cube 2: Hypercube. Perspective projections Cube (3 cube) Tesseract (4 cube) In geometry, a hypercube is an n dimensional analogue of a …   Wikipedia Kd-tree — In computer science, a k d tree (short for k dimensional tree ) is a space partitioning data structure for organizing points in a k dimensional space. k d trees are a useful data structure for several applications, such as searches involving a… …   Wikipedia Dimension — 0d redirects here. For 0D, see 0d (disambiguation). For other uses, see Dimension (disambiguation). From left to right, the square, the cube, and the tesseract. The square is bounded by 1 dimensional lines, the cube by 2 dimensional areas, and… …   Wikipedia Polytope — Not to be confused with polytrope. In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on… …   Wikipedia Simplex — For other uses, see Simplex (disambiguation). A regular 3 simplex or tetrahedron In geometry, a simplex (plural simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n… …   Wikipedia Rectangle — Family Orthotope Type Quadrilateral Edges and vertices 4 Schläfli symbol {}x{} …   Wikipedia Cuboid — For other uses, see Cuboid (disambiguation). In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing (but incompatible) definitions of a cuboid in mathematical literature. In the more… …   Wikipedia MBB — may refer to:* Magandang Balita Biblia, a Tagalog translation of the Holy Bible * Make before break, a type of contact arrangement of an electrical switch, which ensures that when a switch transition happens, the new contact is always made before …   Wikipedia Cross-polytope — In geometry, a cross polytope,[1] orthoplex,[2] hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross polytope are all the permutations of (±1, 0, 0, …, 0). The cross polytope is …   Wikipedia 18+ © Academic, 2000-2024 Contact us: Technical Support, Advertising Dictionaries export, created on PHP, Joomla, Drupal, WordPress, MODx. Mark and share Search through all dictionaries Translate… Search Internet Share the article and excerpts Direct link … Do a right-click on the link above and select “Copy Link”