- Hypercubic honeycomb
-

A regular square tiling.






A partial-filled cubic honeycomb in its regular form.








A checkboard square tiling






A partially-filled cubic honeycomb checkerboard.






An expanded square tiling





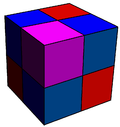
Expanded cubic honeycomb







In geometry, a hypercubic honeycomb is a family of regular honeycombs (tessellations) in n-dimensions with the Schläfli symbols {4,3...3,4} and containing the symmetry of Coxeter group Rn (or B~n-1) for n>=3.
The tessellation is constructed from 4 n-hypercubes per ridge. The vertex figure is a cross-polytope {3...3,4}.
The hypercubic honeycombs are self-dual.
Coxeter named this family as δn+1 for an n-dimensional honeycomb.
Wythoff construction classes by dimension
There are two general forms of the hypercube honeycombs, the regular form with identical hypercubic facets and one semiregular, with alternating hypercube facets, like a checkerboard.
A third form is generated by an expansion operation applied to the regular form, creating facets in place of all lower dimensional elements. For example, an expanded cubic honeycomb has cubic cells centered on the original cubes, on the original faces, on the original edges, on the original vertices, creating 3 colors of cells around in vertex in 1:3:3:1 counts.
A more general class of honeycombs is called, orthotopic honeycombs, with identical topology, but allow each axial direction to have different edge lengths, for example with rectangle and cuboid facets in 2 and 3 dimensions.
δn Name Schläfli symbols Coxeter-Dynkin diagrams Orthotopic
{∞}n
(2m colors, m<n)Regular
{4,3n-1,4}
(1 color)Checkerboard
{4,3n-4,31,1}
(2 colors)Expanded
t0,n-1{4,3n-1,4}
(n colors)δ2 Apeirogon {∞} 


δ3 Square tiling {∞}2
{4,4}





















δ4 Cubic honeycomb {∞}3
{4,3,4}
{4,31,1}





























δ5 Tesseractic honeycomb {∞}4
{4,32,4}
{4,3,31,1}







































δ6 Penteractic honeycomb {∞}5
{4,33,4}
{4,32,31,1}

















































δ7 Hexeractic honeycomb {∞}6
{4,34,4}
{4,33,31,1}



























































δ8 Hepteractic honeycomb {∞}7
{4,35,4}
{4,34,31,1}





































































δ9 Octeractic honeycomb {∞}8
{4,36,4}
{4,35,31,1}















































































δ10 Enneractic honeycomb {∞}9
{4,37,4}
{4,36,31,1}
























































































δ11 Dekeractic honeycomb {∞}10
{4,38,4}
{4,36,31,1}


































































































δn n-hypercubic honeycomb {∞}n
{4,3n-3,4}
{4,3n-4,31,1}... See also
References
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
- pp. 122-123, 1973. (The lattice of hypercubes γn form the cubic honeycombs, δn+1)
- pp. 154-156: Partial truncation or alternation, represented by h prefix: h{4,4}={4,4}; h{4,3,4}={31,1,4}, h{4,3,3,4}={3,3,4,3}
- p. 296, Table II: Regular honeycombs, δn+1
Categories:- Honeycombs (geometry)
- Polytopes
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
Wikimedia Foundation. 2010.
