- Cubic honeycomb
-
Cubic honeycomb 
Type Regular honeycomb Family Hypercube honeycomb Schläfli symbol {4,3,4} Coxeter-Dynkin diagram 






Cell type {4,3} Face type {4} Vertex figure 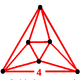
(octahedron)Cells/edge {4,3}4 Faces/edge 44 Cells/vertex {4,3}8 Faces/vertex 412 Edges/vertex 6 Euler characteristic 0 Coxeter groups  , [4,3,4]
, [4,3,4]Dual self-dual Properties vertex-transitive The cubic honeycomb is the only regular space-filling tessellation (or honeycomb) in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron.
It is a self-dual tessellation with Schläfli symbol {4,3,4}. It is part of a multidimensional family of hypercube honeycombs, with Schläfli symbols of the form {4,3,...,3,4}, starting with the square tiling, {4,4} in the plane.
It is one of 28 uniform honeycombs using convex uniform polyhedral cells.
Contents
Related polytopes and tesellations
It is related to the regular 4-polytope tesseract, Schläfli symbol {4,3,3}, which exists in 4-space, and only has 3 cubes around each edge. It's also related to the order-5 cubic honeycomb, Schläfli symbol {4,3,5}, of hyperbolic space with 5 cubes around each edge.
Uniform colorings
There is a large number of uniform colorings, derived from different symmetries. These include:
Coxeter-Dynkin diagram Schläfli symbol Partial
honeycombColors by letters 






{4,3,4} 
1: aaaa/aaaa 








{4,4}xt{∞} 
2: aaaa/bbbb 








t1{4,4}x{∞} 
2: abba/abba 




{4,31,1} 
2: abba/baab 










t{∞}xt{∞}x{∞} 
4: abcd/abcd 






t0,3{4,3,4} 
4: abbc/bccd 










t{∞}xt{∞}xt{∞} 
8: abcd/efgh See also
- List of regular polytopes
- Order-5 cubic honeycomb A hyperbolic cubic honeycomb with 5 cubes per edge
References
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 p.296, Table II: Regular honeycombs
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
- Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
- A. Andreini, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
- Richard Klitzing, 3D Euclidean Honeycombs, x4o3o4o - chon - O1
- Uniform Honeycombs in 3-Space: 01-Chon
Categories:- Honeycombs (geometry)
- Polychora
Wikimedia Foundation. 2010.

