Convex uniform honeycomb

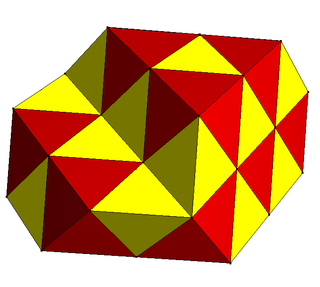The alternated cubic honeycomb is one of 28 space-filling uniform tessellations in Euclidean 3-space, composed of alternating yellow tetrahedra and red octahedra.

In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.

Twenty-eight such honeycombs exist:

• the familiar cubic honeycomb and 7 truncations thereof;
• the alternated cubic honeycomb and 4 truncations thereof;
• 10 prismatic forms based on the uniform plane tilings (11 if including the cubic honeycomb);
• 5 modifications of some of the above by elongation and/or gyration.

They can be considered the three-dimensional analogue to the uniform tilings of the plane.

History

• 1900: Thorold Gosset enumerated the list of semiregular convex polytopes with regular cells (Platonic solids) in his publication On the Regular and Semi-Regular Figures in Space of n Dimensions, including one regular cubic honeycomb, and two semiregular forms with tetrahedra and octahedra.
• 1905: Alfredo Andreini enumerated 25 of these tessellations.
• 1991: Norman Johnson's manuscript Uniform Polytopes identified the complete list of 28.
• 1994: Branko Grünbaum, in his paper Uniform tilings of 3-space, also independently enumerated all 28, after discovering errors in Andreini's publication. He found the 1905 paper, which listed 25, had 1 wrong, and 4 being missing. Grünbaum states in this paper that Norman Johnson deserves priority for achieving the same enumeration in 1991. He also mentions that I. Alexeyev of Russia had contacted him regarding a putative enumeration of these forms, but that Grünbaum was unable to verify this at the time.
• 2006: George Olshevsky, in his manuscript Uniform Panoploid Tetracombs, along with repeating the derived list of 11 convex uniform tilings, and 28 convex uniform honeycombs, expands a further derived list of 143 convex uniform tetracombs (Honeycombs of uniform polychorons in 4-space).

Only 14 of the convex uniform polyhedra appear in these patterns:

• three of the five Platonic solids,
• six of the thirteen Archimedean solids, and
• five of the infinite family of prisms.

Names

This set can be called the regular and semiregular honeycombs. It has been called the Archimedean honeycombs by analogy with the convex uniform (non-regular) polyhedra, commonly called Archimedean solids. Recently Conway has suggested naming the set as the Architectonic tessellations and the dual honeycombs as the Catoptric tessellations.

The individual honeycombs are listed with names given to them by Norman Johnson. (Some of the terms used below are defined in Uniform polychoron#Geometric derivations.)

For cross-referencing, they are given with list indices from [A]ndreini (1-22), [W]illiams(1-2,9-19), [J]ohnson (11-19, 21-25, 31-34, 41-49, 51-52, 61-65), and [G]runbaum(1-28).

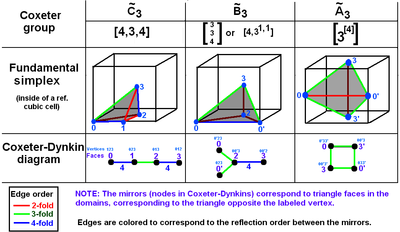
Compact Euclidean uniform tessellations (by their infinite Coxeter group families)

Fundamental domains in a cubic element of three groups.

The fundamental infinite Coxeter groups for 3-space are:

1. The ${\tilde{C}}_3$, [4,3,4], cubic, (8 unique forms plus one alternation)
2. The ${\tilde{B}}_3$, [4,3^1,1], alternated cubic, (11 forms, 3 new)
3. The ${\tilde{A}}_3$ cyclic group, [(3,3,3,3)], (5 forms, one new)

In addition there are 5 special honeycombs which don't have pure reflectional symmetry and are constructed from reflectional forms with elongation and gyration operations.

The total unique honeycombs above are 18.

The prismatic stacks from infinite Coxeter groups for 3-space are:

1. The ${\tilde{C}}_2$x${\tilde{I}}_1$, [4,4]x[∞] prismatic group, (2 new forms)
2. The ${\tilde{H}}_2$x${\tilde{I}}_1$, [6,3]x[∞] prismatic group, (7 unique forms)
3. The ${\tilde{A}}_2$x${\tilde{I}}_1$, (3 3 3)x[∞] prismatic group, (No new forms)
4. The ${\tilde{I}}_1$x${\tilde{I}}_1$x${\tilde{I}}_1$, [∞]x[∞]x[∞] prismatic group, (These all become a cubic honeycomb)

In addition there is one special elongated form of the triangular prismatic honeycomb.

The total unique prismatic honeycombs above (excluding the cubic counted previously) are 10.

Combining these counts, 18 and 10 gives us the total 28 uniform honeycombs.

The C^~₃, [4,3,4] group (cubic)

The regular cubic honeycomb, represented by Schläfli symbol {4,3,4}, offers seven unique derived uniform honeycombs via truncation operations. (One redundant form, the runcinated cubic honeycomb, is included for completeness though identical to the cubic honeycomb.)

Reference Indices	Honeycomb name Coxeter-Dynkin and Schläfli symbols	Cell counts/vertex and positions in cubic honeycomb
		(0)	(1)	(2)	(3)	Solids (Partial)	Frames (Perspective)	Vertex figure
J11,15 A1 W1 G22	cubic t0{4,3,4}				(8) (4.4.4)			octahedron
J12,32 A15 W14 G7	rectified cubic t1{4,3,4}	(2) (3.3.3.3)			(4) (3.4.3.4)			cuboid
J13 A14 W15 G8	truncated cubic t0,1{4,3,4}	(1) (3.3.3.3)			(4) (3.8.8)			square pyramid
J14 A17 W12 G9	cantellated cubic t0,2{4,3,4}	(1) (3.4.3.4)	(2) (4.4.4)		(2) (3.4.4.4)			obilique triangular prism
J11,15	runcinated cubic (same as regular cubic) t0,3{4,3,4}	(1) (4.4.4)	(3) (4.4.4)	(3) (4.4.4)	(1) (4.4.4)			octahedron
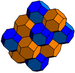
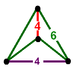
J16 A3 W2 G28	bitruncated cubic t1,2{4,3,4}	(2) (4.6.6)			(2) (4.6.6)			(disphenoid tetrahedron)
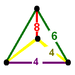
J17 A18 W13 G25	cantitruncated cubic t0,1,2{4,3,4}	(1) (4.6.6)	(1) (4.4.4)		(2) (4.6.8)			irregular tetrahedron
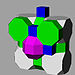
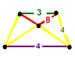
J18 A19 W19 G20	runcitruncated cubic t0,1,3{4,3,4}	(1) (3.4.4.4)	(1) (4.4.4)	(2) (4.4.8)	(1) (3.8.8)			oblique trapezoidal pyramid
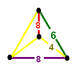
J19 A22 W18 G27	omnitruncated cubic t0,1,2,3{4,3,4}	(1) (4.6.8)	(1) (4.4.8)	(1) (4.4.8)	(1) (4.6.8)			irregular tetrahedron
J21,31,51 A2 W9 G1	alternated cubic h0{4,3,4}	(6) (3.3.3.3)			(8) (3.3.3)			cuboctahedron

B^~₄, [4,3^1,1] group

The ${\tilde{B}}_4$ group offers 11 derived forms via truncation operations, four being unique uniform honeycombs.

The honeycombs from this group are called alternated cubic because the first form can be seen as a cubic honeycomb with alternate vertices removed, reducing cubic cells to tetrahedra and creating octahedron cells in the gaps.

Nodes are indexed left to right as 0,1,0',3 with 0' being below and interchangeable with 0. The alternate cubic names given are based on this ordering.

Referenced indices	Honeycomb name Coxeter-Dynkin diagram	Cells by location (and count around each vertex)				Solids (Partial)	Frames (Perspective)	vertex figure
		(0)	(1)	(0')	(3)
J21,31,51 A2 W9 G1	alternated cubic			(6) (3.3.3.3)	(8) (3.3.3)			cuboctahedron
J22,34 A21 W17 G10	truncated alternated cubic	(1) (3.4.3.4)		(2) (4.6.6)	(2) (3.6.6)			rectangular pyramid
J12,32 A15 W14 G7	rectified cubic (rectified alternate cubic)	(2) (3.4.3.4)		(2) (3.4.3.4)	(2) (3.3.3.3)			cuboid
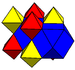
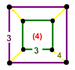
J12,32 A15 W14 G7	rectified cubic (cantellated alternate cubic)	(1) (3.3.3.3)		(1) (3.3.3.3)	(4) (3.4.3.4)			cuboid
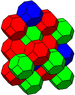
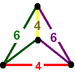
J16 A3 W2 G28	bitruncated cubic (cantitruncated alternate cubic)	(1) (4.6.6)		(1) (4.6.6)	(2) (4.6.6)			isosceles tetrahedron
J13 A14 W15 G8	truncated cubic (bicantellated alternate cubic)	(2) (3.8.8)		(2) (3.8.8)	(1) (3.3.3.3)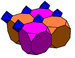			square pyramid
J11,15 A1 W1 G22	cubic (trirectified alternate cubic)	(4) (4.4.4)		(4) (4.4.4)				octahedron
J23 A16 W11 G5	runcinated alternated cubic	(1) cube		(3) (3.4.4.4)	(1) (3.3.3)			tapered triangular prism
J14 A17 W12 G9	cantellated cubic (runcicantellated alternate cubic)	(1) (3.4.4.4)	(2) (4.4.4)	(1) (3.4.4.4)	(1) (3.4.3.4)			obilique triangular prism
J24 A20 W16 G21	cantitruncated alternated cubic (or runcitruncated alternate cubic)	(1) (3.8.8)		(2) (4.6.8)	(1) (3.6.6)			Irregular tetrahedron
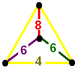
J17 A18 W13 G25	cantitruncated cubic (omnitruncated alternated cubic)	(1) (4.6.8)	(1) (4.4.4)	(1) (4.6.8)	(1) (4.6.6)			irregular tetrahedron

A^~₃, [(3,3,3,3)] group

There are 5 forms^[1] constructed from the ${\tilde{A}}_3$ group, of which only the quarter cubic honeycomb is unique.

Referenced indices	Honeycomb name Coxeter-Dynkin diagram	Cells by location (and count around each vertex)				Solids (Partial)	Frames (Perspective)	vertex figure
		(0)	(1)	(2)	(3)
J21,31,51 A2 W9 G1	alternated cubic		(4) (3.3.3)	(6) (3.3.3.3)	(4) (3.3.3)			cuboctahedron
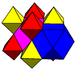
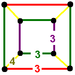
J12,32 A15 W14 G7	rectified cubic	(2) (3.4.3.4)	(1) (3.3.3.3)	(2) (3.4.3.4)	(1) (3.3.3.3)			cuboid
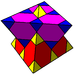
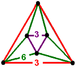
J25,33 A13 W10 G6	quarter cubic	(1) (3.3.3)	(1) (3.3.3)	(3) (3.6.6)	(3) (3.6.6)			triangular antiprism
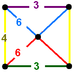
J22,34 A21 W17 G10	truncated alternated cubic	(1) (3.6.6)	(1) (3.4.3.4)	(1) (3.6.6)	(2) (4.6.6)			Rectangular pyramid
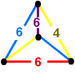
J16 A3 W2 G28	bitruncated cubic	(1) (4.6.6)	(1) (4.6.6)	(1) (4.6.6)	(1) (4.6.6)			isosceles tetrahedron

Nonwythoffian forms (gyrated and elongated)

Three more uniform honeycombs are generated by breaking one or another of the above honeycombs where its faces form a continuous plane, then rotating alternate layers by 60 or 90 degrees (gyration) and/or inserting a layer of prisms (elongation).

The elongated and gyroelongated alternated cubic tilings have the same vertex figure, but are not alike. In the elongated form, each prism meets a tetrahedron at one triangular end and an octahedron at the other. In the gyroelongated form, prisms that meet tetrahedra at both ends alternate with prisms that meet octahedra at both ends.

The gyroelongated triangular prismatic tiling has the same vertex figure as one of the plain prismatic tilings; the two may be derived from the gyrated and plain triangular prismatic tilings, respectively, by inserting layers of cubes.

Referenced indices	symbol	Honeycomb name	cell types (# at each vertex)	Solids (Partial)	Frames (Perspective)	vertex figure
J52 A2' G2	h{4,3,4}:g	gyrated alternated cubic	tetrahedron (8) octahedron (6)			triangular orthobicupola
J61 A? G3	h{4,3,4}:ge	gyroelongated alternated cubic	triangular prism (6) tetrahedron (4) octahedron (3)			-
J62 A? G4	h{4,3,4}:e	elongated alternated cubic	triangular prism (6) tetrahedron (4) octahedron (3)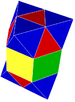
J63 A? G12	{3,6}:g x {∞}	gyrated triangular prismatic	triangular prism (12)
J64 A? G15	{3,6}:ge x {∞}	gyroelongated triangular prismatic	triangular prism (6) cube (4)

Prismatic stacks

Eleven prismatic tilings are obtained by stacking the eleven uniform plane tilings, shown below, in parallel layers. (One of these honeycombs is the cubic, shown above.) The vertex figure of each is an irregular bipyramid whose faces are isosceles triangles.

The C^~₂xI^~₁(∞), [4,4] x [∞], prismatic group

There's only 3 unique honeycombs from the square tiling, but all 6 tiling truncations are listed below for completeness, and tiling images are shown by colors corresponding to each form.

Indices	Coxeter-Dynkin and Schläfli symbols	Honeycomb name	Plane tiling	Solids (Partial)	Tiling
J11,15 A1 G22	{4,4} x {∞}	Cubic (Square prismatic)	(4.4.4.4)
J45 A6 G24	t0,1{4,4} x {∞}	Truncated/Bitruncated square prismatic	(4.8.8)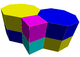
J11,15 A1 G22	t1{4,4} x {∞}	Cubic (Rectified square prismatic)	(4.4.4.4)
J11,15 A1 G22	t0,2{4,4} x {∞}	Cubic (Cantellated square prismatic)	(4.4.4.4)
J45 A6 G24	t0,1,2{4,4} x {∞}	Truncated square prismatic (Omnitruncated square prismatic)	(4.8.8)
J44 A11 G14	s{4,4} x {∞}	Snub square prismatic	(3.3.4.3.4)

The G^~₂xI^~₁(∞), [6,3] x [∞] prismatic group

Indices	Coxeter-Dynkin and Schläfli symbols	Honeycomb name	Plane tiling	Solids (Partial)	Tiling
J42 A5 G26	t0{6,3} x {∞}	Hexagonal prismatic	(63)
J46 A7 G19	t0,1{6,3} x {∞}	Truncated hexagonal prismatic	(3.12.12)
J43 A8 G18	t1{6,3} x {∞}	Trihexagonal prismatic	(3.6.3.6)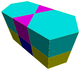
J42 A5 G26	t1,2{6,3} x {∞}	Truncated triangular prismatic Hexagonal prismatic	(6.6.6)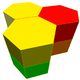
J41 A4 G11	t2{6,3} x {∞}	Triangular prismatic	(36)
J47 A9 G16	t0,2{6,3} x {∞}	Rhombi-trihexagonal prismatic	(3.4.6.4)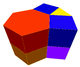
J49 A10 G23	t0,1,2{6,3} x {∞}	Omnitruncated trihexagonal prismatic	(4.6.12)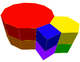
J48 A12 G17	s{6,3} x {∞}	Snub trihexagonal prismatic	(3.3.3.3.6)
J65 A11' G13	{3,6}:e x {∞}	elongated triangular prismatic	(3.3.3.4.4)

Examples

All 28 of these tessellations are found in crystal arrangements.^{[citation needed]}

The alternated cubic honeycomb is of special importance since its vertices form a cubic close-packing of spheres. The space-filling truss of packed octahedra and tetrahedra was apparently first discovered by Alexander Graham Bell and independently re-discovered by Buckminster Fuller (who called it the octet truss and patented it in the 1940s). [2] [3] [4] [5]. Octet trusses are now among the most common types of truss used in construction.

Noncompact forms

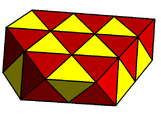
Examples (partially drawn)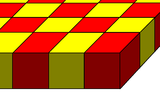

Cubic slab honeycomb	Alternated hexagonal slab honeycomb

If cells are allowed to be uniform tilings, more uniform honeycombs can be defined:

Families:

• ${\tilde{C}}_2$xA₁: [4,4]x[ ] Cubic prismatic slab honeycomb (3 forms)
• ${\tilde{G}}_2$xA₁: [6,3]x[ ] Tri-hexagonal prismatic slab honeycomb (8 forms)
• ${\tilde{A}}_2$xA₁: (3 3 3)x[ ] Triangular prismatic slab (No new forms)
• ${\tilde{I}}_1$xA₁xA₁: [∞]x[ ]x[ ] = Cubic column honeycomb (1 form)
• I₂(p)x${\tilde{I}}_1$: [p]x[∞] Prismatic column honeycomb
• ${\tilde{C}}_2$x${\tilde{C}}_2$xA₁: [∞]x[∞]x[ ] = [4,4]x[ ] - = (Same as cubic slab honeycomb family)

Hyperbolic forms

The {5,3,4} honeycomb in 3D hyperbolic space, viewed in perspective

Main article: Convex uniform honeycombs in hyperbolic space

There are 9 Coxeter group families of compact uniform honeycombs in hyperbolic 3-space, generated as Wythoff constructions, and represented by ring permutations of the Coxeter-Dynkin diagrams for each family.

From these 9 families, there are a total of 76 unique honeycombs generated:

• [3,5,3] : - 9 forms
• [5,3,4] : - 15 forms
• [5,3,5] : - 9 forms
• [5,3^1,1] : - 11 forms (7 overlap with [5,3,4] family, 4 are unique)
• (4 3 3 3) : - 9 forms
• (4 3 4 3) : - 6 forms
• (5 3 3 3) : - 9 forms
• (5 3 4 3) : - 9 forms
• (5 3 5 3) : - 6 forms

The full list of hyperbolic uniform honeycombs has not been proven and an unknown number of non-Wythoffian exist. One known example is in the {3,5,3} family.

There are also 23 noncompact Coxeter groups of rank 4. These families can produce uniform honeycombs with unbounded facets or vertex figure, including ideal vertices at infinity:

Hyperbolic noncompact groups

7	, , , , , ,
7	, , ,, , ,
6	, , , , ,
3	, ,

References

1. ^ [1], A000029 6-1 cases, skipping one with zero marks

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)
• George Olshevsky, (2006, Uniform Panoploid Tetracombs, Manuscript (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
• Branko Grünbaum, (1994) Uniform tilings of 3-space. Geombinatorics 4, 49 - 56.
• Norman Johnson (1991) Uniform Polytopes, Manuscript
• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.  (Chapter 5: Polyhedra packing and space filling)
• Critchlow, Keith (1970). Order in Space: A design source book. Viking Press. ISBN 0-500-34033-1. 
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [6]
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
• A. Andreini, (1905) Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 75–129.
• D. M. Y. Sommerville, (1930) An Introduction to the Geometry of n Dimensions. New York, E. P. Dutton, . 196 pp. (Dover Publications edition, 1958) Chapter X: The Regular Polytopes

External links

• Weisstein, Eric W., "Honeycomb" from MathWorld.
• Uniform Honeycombs in 3-Space VRML models
• Elementary Honeycombs Vertex transitive space filling honeycombs with non-uniform cells.
• Uniform partitions of 3-space, their relatives and embedding, 1999
• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra
• octet truss animation
• Review: A. F. Wells, Three-dimensional nets and polyhedra, H. S. M. Coxeter (Source: Bull. Amer. Math. Soc. Volume 84, Number 3 (1978), 466-470.)
• Richard Klitzing, 3D, Euclidean tesselations