Truncated square tiling

Truncated square tiling
Type	Semiregular tiling
Vertex configuration	4.8.8
Schläfli symbol	t0,1{4,4} t0,1,2{4,4}
Wythoff symbol	2 | 4 4 4 4 2 |
Coxeter-Dynkin
Symmetry	p4m, [4,4], *442
Dual	Tetrakis square tiling
Properties	Vertex-transitive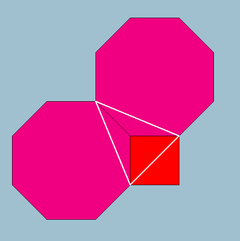
Vertex figure: 4.8.8

In geometry, the truncated square tiling is a semiregular tiling of the Euclidean plane. There is one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon. It has Schläfli symbol of t_0,1{4,4}.

Conway calls it a truncated quadrille, constructed as a truncation operation applied to a square tiling (quadrille).

Other names used for this pattern include Mediterranean tiling and octagonal tiling.

There are 3 regular and 8 semiregular tilings in the plane.

Uniform colorings

There are two distinct uniform colorings of a truncated square tiling. (Naming the colors by indices around a vertex (4.8.8): 122, 123.)

2 colors: 122

3 colors: 123

Related polyhedra and tilings

It is topologically related to the polyhedron truncated octahedron, 4.6.6.

The Pythagorean tiling alternates large and small squares, and may be seen as topologically identical to the truncated square tiling. The squares are rotated 45 degrees and octagons are distorted into squares with mid-edge vertices.

This tiling (with two chiral forms and two uniform colorings) sometimes is called the Pythagorean tiling because its geometry may be used in a proof for the Pythagorean theorem.		This weaving pattern has the same topology as well, with octagons flattened into 3 by 1 rectangles

See also

• Tilings of regular polygons
• List of uniform tilings

References

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 [1]
• Grünbaum, Branko ; and Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-716-71193-1.  (Chapter 2.1: Regular and uniform tilings, p.58-65)
• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. p. 40. ISBN 0-486-23729-X. 

External links

• http://www.decrete.com/stencils/octagontile
• Weisstein, Eric W., "Semiregular tessellation" from MathWorld.
• Richard Klitzing, 2D Euclidean tilings, o4x4x - tosquat - O6