- Bisected hexagonal tiling
-
Bisected hexagonal tiling 
Type Dual semiregular tiling Faces 30-60-90 triangle Face configuration V4.6.12 Symmetry group p6m (*632) Dual truncated trihexagonal tiling Properties face-transitive In geometry, the bisected hexagonal tiling is a tiling of the Euclidean plane. It is constructed by congruent 30-60 degree right triangles with 4, 6, and 12 triangles meeting at each vertex.
It can be seen as an equilateral hexagonal tiling with each hexagon divided into 12 triangles from the center point. (Alternately it can be seen as a bisected triangular tiling divided into 6 triangles, or as an infinite arrangement of lines in six parallel families.)
Conway calls it a kisrhombille[1] for his kis vertex bisector operation applied to the rhombille tiling. More specifically it can be called a 3-6 kisrhombille, to distringuish it from other similar hyperbolic tilings, like 3-7 kisrhombille.
It is labeled V4.6.12 because each right triangle face has three types of vertices: one with 4 triangles, one with 6 triangles, and one with 12 triangles.
Contents
Dual tiling
It is the dual tessellation of the truncated trihexagonal tiling which has one square and one hexagon and one dodecagon at each vertex.
Related polyhedra and tilings
It is topologically related to a polyhedra sequence defined by the face configuration V4.6.2n. This group is special for having all even number of edges per vertex and form bisecting planes through the polyhedra and infinite lines in the plane, and continuing into the hyperbolic plane for any

With an even number of faces at every vertex, these polyhedra and tilings can be shown by alternating two colors so all adjacent faces have different colors.
Each face on these domains also corresponds to the fundamental domain of a symmetry group with order 2,3,n mirrors at each triangle face vertex.
n 2 3 4 5 Tiling space Spherical Face configuration
V4.6.2nV4.6.4 V4.6.6 V4.6.8 V4.6.10 Symmetry group
(Orbifold)D3h (*322)
D6h (*622) full sym.Td (*332)
Oh (*432) full sym.Oh (*432) Ih (*532) Symmetry
fundamental
domain
(Order 12)
(Order 24)
(Order 48)
(Order 60)Polyhedron 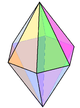



Net 



n 6 7 8 Tiling space Euclidean Hyperbolic Hyperbolic Face configuration
V4.6.2nV4.6.12 V4.6.14 V4.6.16 Symmetry group
(orbifold notation)(*632) (*732) (*832) Tiling 

... Practical uses
The bisected hexagonal tiling is a useful starting point for making paper models of deltahedra, as each of the equilateral triangles can serve as faces, the edges of which adjoin isosceles triangles that can serve as tabs for gluing the model together.
See also
- Tilings of regular polygons
- List of uniform tilings
Notes
- ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 [1] (Chapter 21, Naming Archimedean and Catalan polyhedra and tilings, p288 table)
References
- Grünbaum, Branko ; and Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-716-71193-1. (Chapter 2.1: Regular and uniform tilings, p.58-65)
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. p41
Categories:
Wikimedia Foundation. 2010.

