Truncated icosidodecahedron

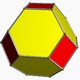
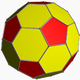
Truncated icosidodecahedron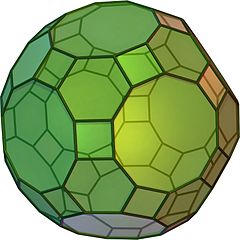
(Click here for rotating model)
Type	Archimedean solid Uniform polyhedron
Elements	F = 62, E = 180, V = 120 (χ = 2)
Faces by sides	30{4}+20{6}+12{10}
Schläfli symbol	t0,1,2{5,3}
Wythoff symbol	2 3 5 |
Coxeter-Dynkin
Symmetry	Ih, [5,3], (*532)
Dihedral Angle	hexagon-decagon: 142.62° square-decagon: 148.28° hexagon-square: 159.095°
References	U28, C31, W16
Properties	Semiregular convex zonohedron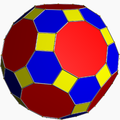
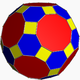
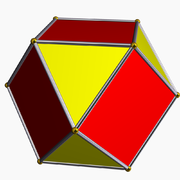
Colored faces	4.6.10 (Vertex figure)
Disdyakis triacontahedron (dual polyhedron)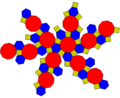	Net

In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.

It has 30 square faces, 20 regular hexagonal faces, 12 regular decagonal faces, 120 vertices and 180 edges – more than any other nonprismatic uniform polyhedron. Since each of its faces has point symmetry (equivalently, 180° rotational symmetry), the truncated icosidodecahedron is a zonohedron.

Other names

Alternate interchangeable names include:

• Truncated icosidodecahedron (Johannes Kepler)
• Rhombitruncated icosidodecahedron (Magnus Wenninger^[1])
• Great rhombicosidodecahedron (Robert Williams,^[2] Peter Cromwell^[3])
• Omnitruncated dodecahedron or icosahedron (Norman Johnson)

The name truncated icosidodecahedron, originally given by Johannes Kepler, is somewhat misleading. If one truncates an icosidodecahedron by cutting the corners off, one does not get this uniform figure: instead of squares the truncation has golden rectangles. However, the resulting figure is topologically equivalent to this and can always be deformed until the faces are regular.

Icosidodecahedron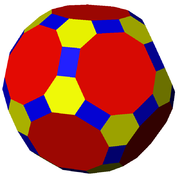

A literal geometric truncation of the icosidodecahedron produces rectangular faces rather than squares.

The alternative name great rhombicosidodecahedron (as well as rhombitruncated icosidodecahedron) refers to the fact that the 30 square faces lie in the same planes as the 30 faces of the rhombic triacontahedron which is dual to the icosidodecahedron. Compare to small rhombicosidodecahedron.

One unfortunate point of confusion is that there is a nonconvex uniform polyhedron of the same name. See nonconvex great rhombicosidodecahedron.

Area and volume

The surface area A and the volume V of the truncated icosidodecahedron of edge length a are:

$\begin{align} A & = 30 \left [ 1 + \sqrt{ 2 \left ( 4 + \sqrt{5} + \sqrt{15+6\sqrt{6}} \right ) } \right ] a^2 \\ & \approx 175.031045a^2 \\ V & = ( 95 + 50\sqrt{5} ) a^3 \approx 206.803399a^3. \\ \end{align}$

Truncated icosidodecahedron is the largest solid among all 13 Archimedean solids with the same side lengths.

Cartesian coordinates

Cartesian coordinates for the vertices of a truncated icosidodecahedron with edge length 2τ − 2, centered at the origin, are all the even permutations of:^[4]

(±1/τ, ±1/τ, ±(3+τ)),

(±2/τ, ±τ, ±(1+2τ)),

(±1/τ, ±τ², ±(−1+3τ)),

(±(-1+2τ), ±2, ±(2+τ)) and

(±τ, ±3, ±2τ),

where τ = (1 + √5)/2 is the golden ratio.

Orthogonal projections

The truncated icosidodecahedron has seven special orthogonal projections, centered on a vertex, on three types of edges, and three types of faces: square, hexagonal and decagonal. The last two correspond to the A₂ and H₂ Coxeter planes.

Orthogonal projections

Centered by	Vertex	Edge 4-6	Edge 4-10	Edge 6-10	Face square	Face hexagon	Face decagon
Image
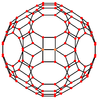
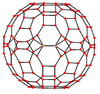
Projective symmetry	[2]+	[2]	[2]	[2]	[2]	[6]	[10]

Spherical tiling

The truncated icosidodecahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.

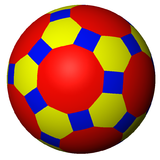
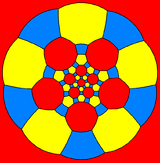
	Decagon-centered	Hexagon-centered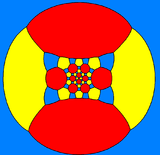	square-centered
Spherical tiling	Stereographic projections (face-centered)

See also

• Spinning great rhombicosidodecahedron
• dodecahedron
• great truncated icosidodecahedron
• icosahedron
• truncated cuboctahedron

Notes

1. ^ Wenninger, (Model 16, p. 30)
2. ^ Williamson (Section 3-9, p. 94)
3. ^ Cromwell (p. 82)
4. ^ Weisstein, Eric W., "Icosahedral group" from MathWorld.

References

• Wenninger, Magnus (1974), Polyhedron Models, Cambridge University Press, ISBN 978-0-521-09859-5, MR0467493 
• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. 
• Cromwell, P.; Polyhedra, CUP hbk (1997), pbk. (1999).
• Eric W. Weisstein, GreatRhombicosidodecahedron (Archimedean solid) at MathWorld.
• Richard Klitzing, 3D convex uniform polyhedra, x3x5x - grid

External links

• Editable printable net of a truncated icosidodecahedron with interactive 3D view
• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra

Archimedean solids
Truncated tetrahedron Truncated cube Truncated octahedron Truncated dodecahedron Truncated icosahedron Cuboctahedron Icosidodecahedron Snub cube Rhombi- cuboctahedron Truncated cuboctahedron Truncated icosidodecahedron Rhomb- icosidodecahedron Snub dodecahedron