Deltoidal hexecontahedron

Deltoidal hexecontahedron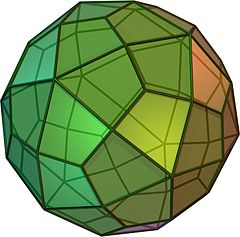
Click on picture for large version spinning version
Type	Catalan
Face polygon	kite
Faces	60
Edges	120
Vertices	62 = 12 + 20 + 30
Face configuration	V3.4.5.4
Symmetry group	Ih, [5,3]+, 532
Dihedral angle	154° 8'
Properties	convex, face-transitive
rhombicosidodecahedron (dual polyhedron)	Net

In geometry, a deltoidal hexecontahedron (also sometimes called a trapezoidal hexecontahedron, a strombic hexecontahedron, or a tetragonal hexacontahedron) is a catalan solid which looks a bit like an overinflated dodecahedron. It is sometimes also called the trapezoidal hexecontahedron or strombic hexecontahedron. Its dual polyhedron is the rhombicosidodecahedron.

The 60 faces are deltoids or kites (not trapezoidal). The short and long edges of each kite are in the ratio 1.00:1.54.

It is the only Archimedean dual which does not have a Hamiltonian path among its vertices.

See also

• Deltoidal icositetrahedron

References

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.  (Section 3-9)
• The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 [1] (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, page 286, tetragonal hexecontahedron)

External links

• Eric W. Weisstein, DeltoidalHexecontahedron and Hamiltonian path (Catalan solid) at MathWorld.
• Deltoidal Hexecontahedron (Trapezoidal Hexecontrahedron) -- Interactive Polyhedron Model

This polyhedron-related article is a stub. You can help Wikipedia by expanding it.v · Categories: Polyhedron stubs Catalan solids Wikimedia Foundation. 2010. Игры ⚽ Поможем сделать НИР Disdyakis dodecahedron Mandalay Bay Resort and Casino Look at other dictionaries: Medial deltoidal hexecontahedron — Type Star polyhedron Elements F = 60, E = 120 V = 54 (χ = −6) Symmetry group Ih, [5,3], *532 …   Wikipedia Deltoidal icositetrahedron — Click on picture for large version. Click here for spinning version. Type Catalan Face polygon kite Faces 24 …   Wikipedia Medial pentagonal hexecontahedron — Type Star polyhedron Elements F = 60, E = 150 V = 84 (χ = −6) Symmetry group I, [5,3]+, 532 …   Wikipedia Catalanische Körper — Ein catalanischer Körper oder auch dual archimedischer Körper ist ein Körper, der sich zu einem archimedischen Körper dual verhält. So ist zum Beispiel das Rhombendodekaeder dual zum Kuboktaeder. Benannt sind catalanische Körper nach dem… …   Deutsch Wikipedia Dual-Archimedischer Körper — Ein catalanischer Körper oder auch dual archimedischer Körper ist ein Körper, der sich zu einem archimedischen Körper dual verhält. So ist zum Beispiel das Rhombendodekaeder dual zum Kuboktaeder. Benannt sind catalanische Körper nach dem… …   Deutsch Wikipedia Nonconvex great rhombicosidodecahedron — Type Uniform star polyhedron Elements F = 62, E = 120 V = 60 (χ = 2) Faces by sides 20{3}+30{4}+12{5/2} …   Wikipedia Kite (geometry) — Kite A kite showing its equal sides and its inscribed circle. Type Quadrilateral Edges and vertices 4 Symmetry group D1 (*) In Euclid …   Wikipedia Snub dodecadodecahedron — Type Uniform star polyhedron Elements F = 84, E = 150 V = 60 (χ = −6) Faces by sides 60{3}+12{5}+12{5/2} Wythoff symbol …   Wikipedia Dodecadodecahedron — Type Uniform star polyhedron Elements F = 24, E = 60 V = 30 (χ = −6) Faces by sides 12{5}+12{5/2} Wythoff symbol …   Wikipedia Truncated great dodecahedron — Type Uniform star polyhedron Elements F = 24, E = 90 V = 60 (χ = −6) Faces by sides 12{5/2}+12{10} Wythof …   Wikipedia 18+ © Academic, 2000-2024 Contact us: Technical Support, Advertising Dictionaries export, created on PHP, Joomla, Drupal, WordPress, MODx. Mark and share Search through all dictionaries Translate… Search Internet Share the article and excerpts Direct link … Do a right-click on the link above and select “Copy Link”