Kite (geometry)

Kite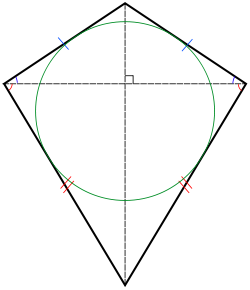
A kite showing its equal sides and its inscribed circle.
Type	Quadrilateral
Edges and vertices	4
Symmetry group	D1 (*)

In Euclidean geometry a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are next to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite each other rather than next to each other. Kite quadrilaterals are named for the wind-blown, flying kites, which often have this shape and which are in turn named for a bird. Kites are also known as deltoids, but the word "deltoid" may also refer to a deltoid curve, an unrelated geometric object.

A kite, as defined above, may be either convex or concave, but the word "kite" is often restricted to the convex variety. A concave kite is sometimes called a "dart" or "arrowhead", and is a type of pseudotriangle.

Special cases

If all four sides of a kite have the same length (that is, if the kite is equilateral), it must be a rhombus.

If a kite is equiangular, meaning that all four of its angles are equal, then it must also be equilateral and thus a square.

Among all quadrilaterals, the shape that has the greatest ratio of its perimeter to its diameter is a kite with angles π/3, 5π/12, 5π/6, 5π/12.^[1]

The kites that are also cyclic quadrilaterals (i.e. the kites that can be inscribed in a circle) are exactly the ones formed from two congruent right triangles. That is, for these kites the two equal angles on opposite sides of the symmetry axis are each 90 degrees.^[2] These shapes are called right kites.^[3]

Characterizations

A quadrilateral is a kite if and only if one of the following statements is true:

• One diagonal is the perpendicular bisector of the other diagonal.^[4] (In the concave case it is the extension of one of the diagonals.)
• One diagonal divides the quadrilateral into two congruent triangles.

Symmetry

In a kite, there exists a pair of opposite congruent angles. One diagonal in a kite bisects a pair of opposite angles.^[4]

The kites are the quadrilaterals that have an axis of symmetry along one of their diagonals.^[5] Any non-self-crossing quadrilateral that has an axis of symmetry must be either a kite (if the axis of symmetry is a diagonal) or an isosceles trapezoid (if the axis of symmetry passes through the midpoints of two sides); these include as special cases the rhombus and the rectangle respectively, which have two axes of symmetry each, and the square which is both a kite and an isosceles trapezoid and has four axes of symmetry.^[5] If crossings are allowed, the list of quadrilaterals with axes of symmetry must be expanded to also include the antiparallelograms. Kites and isosceles trapezoids are dual: the polar figure of a kite is an isosceles trapezoid, and vice versa.^[6]

Area

Every kite is orthodiagonal, meaning that its two diagonals are at right angles to each other. Moreover, one of the two diagonals (the symmetry axis) is the perpendicular bisector of the other, and is also the angle bisector of the two angles it meets.^[5] As is true more generally for any orthodiagonal quadrilateral, the area K of a kite may be calculated as half the product of the lengths of the diagonals p and q:

$K =\frac{p \cdot q}{2}.$

Alternatively, if a and b are the lengths of two unequal sides, and θ is the angle between unequal sides, then the area is

$\displaystyle K = ab \cdot \sin{ \theta}.$

One of the two diagonals of a convex kite divides it into two isosceles triangles; the other (the axis of symmetry) divides the kite into two congruent triangles.^[5] The two interior angles of a kite that are on opposite sides of the symmetry axis are equal.

Additional properties

Every convex kite has an inscribed circle; that is, there exists a circle that is tangent to all four sides. Therefore, every convex kite is a tangential quadrilateral. Additionally, if a convex kite is not a rhombus, there is another circle, outside the kite, tangent to the lines that pass through its four sides; therefore, every convex kite that is not a rhombus is an ex-tangential quadrilateral. For every concave kite there exist two circles tangent to all four (possibly extended) sides: one is interior to the kite and touches the two sides opposite from the concave angle, while the other circle is exterior to the kite and touches the kite on the two edges incident to the concave angle.^[7]

A tangential quadrilateral is a kite if and only if any one of the following conditions is true:^[8]

• The area is one half the product of the diagonals
• The diagonals are perpendicular
• The two line segments connecting opposite points of tangency have equal length
• One pair of opposite tangent lengths have equal length
• The bimedians have equal length
• The products of opposite sides are equal
• The center of the incircle lies on the longest diagonal

Thus the kites are exactly the quadrilaterals that are both orthodiagonal and tangential.

Tilings and polyhedra

All kites tile the plane by repeated inversion around the midpoints of their edges, as do more generally all quadrilaterals. A kite with angles π/3, π/2, 2π/3, π/2 can also tile the plane by repeated reflection across its edges; the resulting tessellation, the deltoidal trihexagonal tiling, superposes a tessellation of the plane by regular hexagons and isosceles triangles.^[9] The deltoidal icositetrahedron, deltoidal hexecontahedron, and trapezohedra are polyhedra with congruent kite-shaped facets. There are an infinite number of uniform tilings of the hyperbolic plane by kites, the simplest of which is the deltoidal triheptagonal tiling.

Kites and darts in which the two isosceles triangles forming the kite have apex angles of 2π/5 and 4π/5 represent one of two sets of essential tiles in the Penrose tiling, an aperiodic tiling of the plane discovered by mathematical physicist Roger Penrose.

Deltoidal icositetrahedron

Deltoidal hexecontahedron

Deltoidal trihexagonal tiling

Deltoidal triheptagonal tiling

See also

• Orthodiagonal quadrilateral
• Rhombus
• Square (geometry)
• Tangential quadrilateral

References

1. ^ Ball, D. G. (1973), "A generalisation of π", Mathematical Gazette (The Mathematical Association) 57 (402): 298–303, doi:10.2307/3616052, JSTOR 3616052 ; Griffiths, David; Culpin, David (1975), "Pi-optimal polygons", Mathematical Gazette (The Mathematical Association) 59 (409): 165–175, doi:10.2307/3617699, JSTOR 3617699 .
2. ^ Gant, P. (1944), "A note on quadrilaterals", Mathematical Gazette (The Mathematical Association) 28 (278): 29–30, doi:10.2307/3607362, JSTOR 3607362 .
3. ^ De Villiers, Michael (1994), "The role and function of a hierarchical classification of quadrilaterals", For the learning of mathematics 14 (1): 11–18, JSTOR 40248098 .
4. ^ ^{a b} Zalman Usiskin and Jennifer Griffin, "The Classification of Quadrilaterals. A Study of Definition", Information Age Publishing, 2008, pp. 51-52.
5. ^ ^{a b c d} Halsted, George Bruce (1896), "Chapter XIV. Symmetrical Quadrilaterals", Elementary Synthetic Geometry, J. Wiley & sons, pp. 49–53, http://books.google.com/books?id=H3ALAAAAYAAJ&pg=PA49 .
6. ^ Robertson, S. A. (1977), "Classifying triangles and quadrilaterals", Mathematical Gazette (The Mathematical Association) 61 (415): 38–49, doi:10.2307/3617441, JSTOR 3617441 .
7. ^ Wheeler, Roger F. (1958), "Quadrilaterals", Mathematical Gazette (The Mathematical Association) 42 (342): 275–276, doi:10.2307/3610439, JSTOR 3610439 .
8. ^ Josefsson, Martin (2011), "When is a Tangential Quadrilateral a Kite?", Forum Geometricorum 11: 165-174, http://forumgeom.fau.edu/FG2011volume11/FG201117.pdf .
9. ^ See Weisstein, Eric W., "Polykite" from MathWorld..

External links

• Weisstein, Eric W., "Kite" from MathWorld.
• Kite definition and area formulae with interactive animations at Mathopenref.com