Tangential quadrilateral

An example of a tangential quadrilateral

In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle. Because tangential quadrilaterals can be drawn surrounding or circumscribing their incircles, they are also sometimes called circumscribable quadrilaterals. Another name for the same class of quadrilaterals is inscriptable quadrilaterals.

Special cases

Examples of tangential quadrilaterals are squares, rhombi, and kites. The kites are exactly the tangential quadrilaterals that are also orthodiagonal.^[1] If a quadrilateral is both tangential and cyclic, it is called a bicentric quadrilateral.

Characterizations

Chao and Simeonov's characterization in terms of the radii of circles within each of four triangles

In a tangential quadrilateral, the four angle bisectors meet at the center of the inscribed circle, and conversely a convex quadrilateral in which the four angle bisectors meet at a point must be tangential.

In a tangential quadrilateral, according to the Pitot theorem, the two pairs of opposite sides add to the same total length, which equals the semiperimeter of the quadrilateral:

$a + c = b + d = \frac{a + b + c + d}{2} = s.$

Conversely a convex quadrilateral in which a + c = b + d must be tangential.

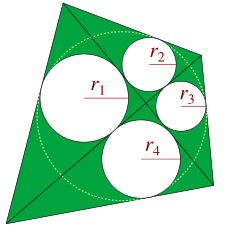
Chao and Simeonov^[2] observed another characterization of tangential quadrilaterals. The two diagonals of any convex quadrilateral partition the quadrilateral into four triangles. Let r₁, r₂, r₃, and r₄ denote the radii of the circles inscribed in the four successively adjacent triangles; then the quadrilateral is tangential if and only if

$\frac{1}{r_1}+\frac{1}{r_3}=\frac{1}{r_2}+\frac{1}{r_4}.$

If opposite sides in a convex quadrilateral ABCD intersect at E and F, then it is tangential if and only if^[3]

$\displaystyle AE-EC=AF-FC.$

This characterization is almost the same as one of the equalities in Urquhart’s Theorem. The only differences are the signs on both sides; in Urquhart’s Theorem there are sums instead of differences.

Area

Tangential quadrilateral with inradius r.

The area K of a tangential quadrilateral is

$\displaystyle K = r \cdot s,$

where s is the semiperimeter described above and r is the circle's radius (called the inradius).

A trigonometric formula for the area is^[4]

$\displaystyle K = \sqrt{abcd} \sin \frac{B+D}{2}$

where B and D are opposite angles. For given side lengths, the area is maximum when the quadrilateral is also cyclic and hence a bicentric quadrilateral. Then $K = \sqrt{abcd}$ since opposite angles are supplementary angles.

In fact, the area can be expressed in terms of only two sides and two opposite angles as^[5]

$K=ab\sin{\frac{B}{2}}\csc{\frac{D}{2}}\sin \frac{B+D}{2}.$

Another area formula is^[5]

$K=\tfrac{1}{2}(ac-bd)\tan{\theta},$

where θ is the angle between the diagonals, and still another is

$\displaystyle K = \tfrac{1}{2}\sqrt{p^2q^2-(ac-bd)^2}$

which gives the area in terms of the diagonals p, q and the sides a, b, c, d of the quadrilateral.

The area K can also be expressed in terms of the four tangent lengths. (The tangent length from any vertex is the distance from that vertex to either of the points where the incircle is tangent to the sides emanating from that vertex). If these are e, f, g, h, then the tangential quadrilateral has the area^[1]

$\displaystyle K=\sqrt{(e+f+g+h)(efg+fgh+ghe+hef)}.$

Inradius

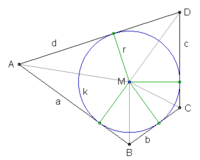
The inradius in a tangential quadrilateral with consecutive sides a, b, c, d is given by

$r=\frac{K}{a+c}=\frac{K}{b+d}$

where K is the area of the quadrilateral. For a tangential quadrilateral with given sides, the inradius is maximum when the quadrilateral is also cyclic (and hence a bicentric quadrilateral).

In terms of the tangent lengths, the incircle has radius^[6]:Lemma2

$\displaystyle r=\sqrt{\frac{efg+fgh+ghe+hef}{e+f+g+h}}.$

Diagonals and tangency chords

The lengths of the diagonals p and q are in terms of the tangent lengths^[6]:Lemma3

$\displaystyle p=\sqrt{\frac{e+g}{f+h}((e+g)(f+h)+4fh)},$

$\displaystyle q=\sqrt{\frac{f+h}{e+g}((e+g)(f+h)+4eg)}.$

The two line segmets that connect the points of tangency of the incircle at opposite sides of the tangential quadrilateral are called the tangency chords. The lengths k and l of these are^[1]

$\displaystyle k=\frac{2(efg+fgh+ghe+hef)}{\sqrt{(e+f)(g+h)(e+g)(f+h)}},$

$\displaystyle l=\frac{2(efg+fgh+ghe+hef)}{\sqrt{(e+h)(f+g)(e+g)(f+h)}}.$

Other properties

• The line segments between the center of the inscribed circle and the points where it is tangent to the quadrilateral partition the quadrilateral into kites.

• The two diagonals and the two tangency chords are concurrent.^[7] One way to see this is as a limiting case of Brianchon's theorem, which states that a hexagon all of whose sides are tangent to a single conic section has three diagonals that meet at a point. From a tangential quadrilateral, one can form a hexagon with two 180° angles, by placing two new vertices at two opposite points of tangency; all six of the sides of this hexagon lie on lines tangent to the inscribed circle, so its diagonals meet at a point. But two of these diagonals are the same as the diagonals of the tangential quadrilateral, and the third diagonal of the hexagon is the line through two opposite points of tangency. Repeating this same argument with the other two points of tangency completes the proof of the result.

• If a four-bar linkage is made in the form of a tangential quadrilateral, then it will remain tangential no matter how the linkage is flexed, provided the quadrilateral remains convex.^[8]

• In a tangential quadrilateral ABCD, the incircles in triangles ABC and ADC are tangent to each other.^[3]

• If a line cuts a tangential quadrilateral into two polygons with equal areas and equal perimeters, then that line passes through the incenter.^[3]

• If M and N are the midpoints of the diagonals in a tangential quadrilateral with incenter I, then the points M, I, and N are collinear.^[3]:p.42

• If the incircle is tangent to the sides AB, BC, CD, DA at X, Y, Z, W respectively, then the lines XY, WZ and AC are concurrent.^[9]:p.11

• If I is the center of the incircle in tangential quadrilateral ABCD, then^[9]:p.16

$IA\cdot IC+IB\cdot ID=\sqrt{AB\cdot BC\cdot CD\cdot DA}.$

• The center I of the incircle in tangential quadrilateral ABCD coincides with the centroid of the quadrilateral if and only if $IA\cdot IC=IB\cdot ID.$^[9]:p.22

Conditions for a tangential quadrilateral to be another type of quadrilateral

A tangential quadrilateral is a rhombus if and only if its opposite angles are equal.^[10]

If the inscribed circle is tangent to the quadrilateral at points T, U, V, W in sequence, then the tangential quadrilateral is also cyclic (and hence bicentric) if and only if TV is perpendicular to UW.^[11]

A tangential quadrilateral is a kite if and only if any one of the following conditions is true:^[12]

• The area is one half the product of the diagonals
• The diagonals are perpendicular
• The two line segments connecting opposite points of tangency have equal length
• One pair of opposite tangent lengths have equal length
• The bimedians have equal length
• The products of opposite sides are equal
• The center of the incircle lies on the longest diagonal

See also

• Bicentric quadrilateral
• Cyclic quadrilateral
• Ex-tangential quadrilateral
• Kite
• Orthodiagonal quadrilateral
• Rhombus

References

1. ^ ^{a b c} Josefsson, Martin (2010), "Calculations concerning the tangent lengths and tangency chords of a tangential quadrilateral", Forum Geometricorum 10: 119–130, http://forumgeom.fau.edu/FG2010volume10/FG201013.pdf .
2. ^ Chao, Wu Wei; Simeonov, Plamen (2000), "When quadrilaterals have inscribed circles (solution to problem 10698)", American Mathematical Monthly 107 (7): 657–658, doi:10.2307/2589133 .
3. ^ ^{a b c d} Andreescu, Titu and Enescu, Bogdan, Mathematical Olympiad Treasures, Birkhäuser, 2006, pp. 67-68.
4. ^ Siddons, A. W., and R. T. Hughes, Trigonometry, Cambridge Univ. Press, 1929: p. 203.
5. ^ ^{a b} Durell, C. V. and Robson, A., Advanced Trigonometry, Dover reprint, 2003, pp. 29-30.
6. ^ ^{a b} Hajja, Mowaffaq (2008), "A condition for a circumscriptible quadrilateral to be cyclic", Forum Geometricorum 8: 103–106, http://forumgeom.fau.edu/FG2008volume8/FG200814.pdf .
7. ^ Yiu, Paul, Euclidean Geometry, [1], 1998, p. 156.
8. ^ Barton, Helen (1925), "On a circle attached to a collapsible four-bar", American Mathematical Monthly 33 (9): 462–465, JSTOR 2299611 .
9. ^ ^{a b c} Darij Grinberg, Circumscribed quadrilaterals revisited, 2008, [2]
10. ^ De Villiers, Michael, Equiangular cyclic and equilateral circumscribed polygons", Mathematical Gazette 95, March 2011, 102-107.
11. ^ Bryant, Victor, and Duncan, John; "Wheels within wheels", Mathematical Gazette 94, November 2010, 502-505.
12. ^ Josefsson, Martin (2011), "When is a Tangential Quadrilateral a Kite?", Forum Geometricorum 11: 165-174, http://forumgeom.fau.edu/FG2011volume11/FG201117.pdf .

External links

• Weisstein, Eric W., "Tangential Quadrilateral" from MathWorld.