Bipyramid

For Dipyramid, see mountain and Dipyramid (Alaska).

Set of bipyramids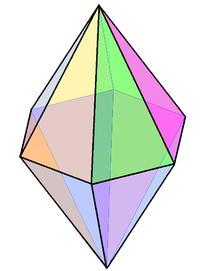
(Example hexagonal form)
Faces	2n triangles
Edges	3n
Vertices	n + 2
Face configuration	V4.4.n
Symmetry group	Dnh, [n,2], (*22n)
Dual polyhedron	n-gonal prism
Properties	convex, face-transitive
Net

An n-gonal bipyramid or dipyramid is a polyhedron formed by joining an n-gonal pyramid and its mirror image base-to-base.

The referenced n-gon in the name of the bipyramids is not an external face but an internal one, existing on the primary symmetry plane which connects the two pyramid halves.

The face-transitive bipyramids are the dual polyhedra of the uniform prisms and will generally have isosceles triangle faces.

A bipyramid can be projected on a sphere or globe as n equally spaced lines of longitude going from pole to pole, and bisected by a line around the equator.

Bipyramid faces, projected as spherical triangles, represent the fundamental domains in the dihedral symmetry D_nh.

Volume

The volume of a bipyramid is $V = \frac{2}{3} Bh$ where B is the area of the base and h the height from the base to the apex. This works for any location of the apex, provided that h is measured as the perpendicular distance from the plane which contains the base.

The volume of a bipyramid whose base is a regular n-sided polygon with side length s and whose height is h is therefore:

$V = \frac{n}{6}hs^2 \cot\frac{\pi}{n}$

Equilateral triangle bipyramids

Only three kinds of bipyramids can have all edges of the same length (which implies that all faces are equilateral triangles, and thus the bipyramid is a deltahedron): the triangular, tetragonal, and pentagonal bipyramids. The tetragonal bipyramid with identical edges, or regular octahedron, counts among the Platonic solids, while the triangular and pentagonal bipyramids with identical edges count among the Johnson solids (J12 and J13).

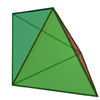
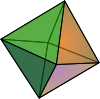
Triangular bipyramid	Square bipyramid (Octahedron)	Pentagonal bipyramid

Forms

1. Triangular bipyramid - 6 faces - dual triangular prism
2. Square bipyramid (the regular octahedron is a special case) - 8 faces - dual cube
3. Pentagonal bipyramid - 10 faces - dual pentagonal prism
4. Hexagonal bipyramid - 12 faces - dual hexagonal prism
5. Heptagonal bipyramid - 14 faces - dual heptagonal prism
6. Octagonal bipyramid - 16 faces - dual octagonal prism
7. Enneagonal bipyramid - 18 faces - dual enneagonal prism
8. Decagonal bipyramid - 20 faces - dual decagonal prism

• ...n-gonal bipyramid - 2n faces - dual n-gonal prism

3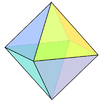

4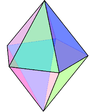

5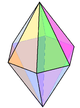

6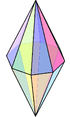

8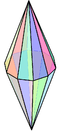

10

Symmetry groups

If the base is regular and the line through the apexes intersects the base at its center, the symmetry group of the n-agonal bipyramid has dihedral symmetry D_nh of order 4n, except in the case of a regular octahedron, which has the larger octahedral symmetry group O_h of order 48, which has three versions of D_4h as subgroups. The rotation group is D_n of order 2n, except in the case of a regular octahedron, which has the larger symmetry group O of order 24, which has three versions of D₄ as subgroups.

Star bipyramids

Self-intersecting bipyramids exist with a star polygon central figure, defined by triangular faces connecting each polygon edge to these two points.

For example, a pentagrammic dipyramid is an isohedral star polyhedron composed of 10 intersecting isoceles triangles. It is the dual to the pentagrammic prism.

Higher dimensions

In general, a bipyramid can be seen as an n-polytope constructed with a (n-1)-polytope in a hyperplane with two points in opposite directions, equal distance perpendicular from the hyperplane. If the (n-1)-polytope is a regular polytope, it will have identical pyramids facets.

See also

• Trapezohedron

External links

• Weisstein, Eric W., "Dipyramid" from MathWorld.
• Olshevsky, George, Bipyramid at Glossary for Hyperspace.
• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra
  • VRML models (George Hart) <3> <4> <5> <6> <7> <8> <9> <10>
    • Conway Notation for Polyhedra Try: "dPn", where n = 3, 4, 5, 6, ... example "dP4" is an octahedron.