- Johnson solid
-
The elongated square gyrobicupola (J37), a Johnson solid
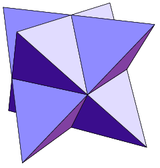This 24 equilateral triangle example is not a Johnson solid because it is not convex. (This is actually a stellation, the only one possible for the octahedron.)
This 24-square example is not a Johnson solid because it is not strictly convex (has 180° dihedral angles.)In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around each vertex. An example of a Johnson solid is the square-based pyramid with equilateral sides (J1); it has 1 square face and 4 triangular faces.
As in any strictly convex solid, at least three faces meet at every vertex, and the total of their angles is less than 360 degrees. Since a regular polygon has angles at least 60 degrees, it follows that at most five faces meet at any vertex. The pentagonal pyramid (J2) is an example that actually has a degree-5 vertex.
Although there is no obvious restriction that any given regular polygon cannot be a face of a Johnson solid, it turns out that the faces of Johnson solids always have 3, 4, 5, 6, 8, or 10 sides.
In 1966, Norman Johnson published a list which included all 92 solids, and gave them their names and numbers. He did not prove that there were only 92, but he did conjecture that there were no others. Victor Zalgaller in 1969 proved that Johnson's list was complete.
Of the Johnson solids, the elongated square gyrobicupola (J37) is unique in being locally vertex-uniform: there are 4 faces at each vertex, and their arrangement is always the same: 3 squares and 1 triangle. However, it is not vertex-transitive, as it has different isometry at different vertices, making it a Johnson solid rather than an Archimedean solid.
Contents
Names
The names are listed below and are more descriptive than they sound. Most of the Johnson solids can be constructed from the first few (pyramids, cupolae, and rotunda), together with the Platonic and Archimedean solids, prisms, and antiprisms.
- Bi- means that two copies of the solid in question are joined base-to-base. For cupolae and rotundae, they can be joined so that like faces (ortho-) or unlike faces (gyro-) meet. In this nomenclature, an octahedron would be a square bipyramid, a cuboctahedron would be a triangular gyrobicupola, and an icosidodecahedron would be a pentagonal gyrobirotunda.
- Elongated means that a prism has been joined to the base of the solid in question or between the bases of the solids in question. A rhombicuboctahedron would be an elongated square orthobicupola.
- Gyroelongated means that an antiprism has been joined to the base of the solid in question or between the bases of the solids in question. An icosahedron would be a gyroelongated pentagonal bipyramid.
- Augmented means that a pyramid or cupola has been joined to a face of the solid in question.
- Diminished means that a pyramid or cupola has been removed from the solid in question.
- Gyrate means that a cupola on the solid in question has been rotated so that different edges match up, as in the difference between ortho- and gyrobicupolae.
The last three operations — augmentation, diminution, and gyration — can be performed more than once on a large enough solid. We add bi- to the name of the operation to indicate that it has been performed twice. (A bigyrate solid has had two of its cupolae rotated.) We add tri- to indicate that it has been performed three times. (A tridiminished solid has had three of its pyramids or cupolae removed.)
Sometimes, bi- alone is not specific enough. We must distinguish between a solid that has had two parallel faces altered and one that has had two oblique faces altered. When the faces altered are parallel, we add para- to the name of the operation. (A parabiaugmented solid has had two parallel faces augmented.) When they are not, we add meta- to the name of the operation. (A metabiaugmented solid has had 2 oblique faces augmented.)
Enumeration
Jn Solid name Net Image V E F F3 F4 F5 F6 F8 F10 Symmetry group 1 Square pyramid 
5 8 5 4 1 C4v 2 Pentagonal pyramid 
6 10 6 5 1 C5v 3 Triangular cupola 
9 15 8 4 3 1 C3v 4 Square cupola 
12 20 10 4 5 1 C4v 5 Pentagonal cupola 
15 25 12 5 5 1 1 C5v 6 Pentagonal rotunda 
20 35 17 10 6 1 C5v 7 Elongated triangular pyramid (or elongated tetrahedron) 
7 12 7 4 3 C3v 8 Elongated square pyramid (or augmented cube)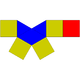 
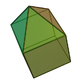
9 16 9 4 5 C4v 9 Elongated pentagonal pyramid 
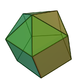
11 20 11 5 5 1 C5v 10 Gyroelongated square pyramid 
9 20 13 12 1 C4v 11 Gyroelongated pentagonal pyramid (or diminished icosahedron) 
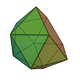
11 25 16 15 1 C5v 12 Triangular bipyramid 
5 9 6 6 D3h 13 Pentagonal bipyramid 
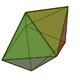
7 15 10 10 D5h 14 Elongated triangular bipyramid 
8 15 9 6 3 D3h 15 Elongated square bipyramid
(or biaugmented cube)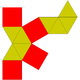
10 20 12 8 4 D4h 16 Elongated pentagonal bipyramid 
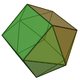
12 25 15 10 5 D5h 17 Gyroelongated square bipyramid 
10 24 16 16 D4d 18 Elongated triangular cupola 
15 27 14 4 9 1 C3v 19 Elongated square cupola
(diminished rhombicuboctahedron)
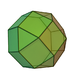
20 36 18 4 13 1 C4v 20 Elongated pentagonal cupola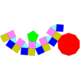 
25 45 22 5 15 1 1 C5v 21 Elongated pentagonal rotunda 
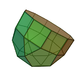
30 55 27 10 10 6 1 C5v 22 Gyroelongated triangular cupola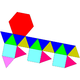 
15 33 20 16 3 1 C3v 23 Gyroelongated square cupola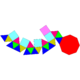 
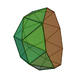
20 44 26 20 5 1 C4v 24 Gyroelongated pentagonal cupola 
25 55 32 25 5 1 1 C5v 25 Gyroelongated pentagonal rotunda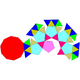 
30 65 37 30 6 1 C5v 26 Gyrobifastigium 
8 14 8 4 4 D2d 27 Triangular orthobicupola
(gyrate cuboctahedron)
12 24 14 8 6 D3h 28 Square orthobicupola 
16 32 18 8 10 D4h 29 Square gyrobicupola 
16 32 18 8 10 D4d 30 Pentagonal orthobicupola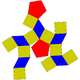 
20 40 22 10 10 2 D5h 31 Pentagonal gyrobicupola 
20 40 22 10 10 2 D5d 32 Pentagonal orthocupolarotunda 
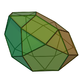
25 50 27 15 5 7 C5v 33 Pentagonal gyrocupolarotunda 
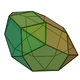
25 50 27 15 5 7 C5v 34 Pentagonal orthobirotunda
(gyrate icosidodecahedron)
30 60 32 20 12 D5h 35 Elongated triangular orthobicupola 
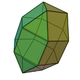
18 36 20 8 12 D3h 36 Elongated triangular gyrobicupola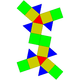 
18 36 20 8 12 D3d 37 Elongated square gyrobicupola
(gyrate rhombicuboctahedron)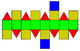
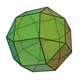
24 48 26 8 18 D4d 38 Elongated pentagonal orthobicupola 
30 60 32 10 20 2 D5h 39 Elongated pentagonal gyrobicupola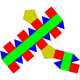 
30 60 32 10 20 2 D5d 40 Elongated pentagonal orthocupolarotunda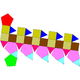 
35 70 37 15 15 7 C5v 41 Elongated pentagonal gyrocupolarotunda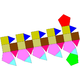 
35 70 37 15 15 7 C5v 42 Elongated pentagonal orthobirotunda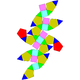 
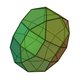
40 80 42 20 10 12 D5h 43 Elongated pentagonal gyrobirotunda 
40 80 42 20 10 12 D5d 44 Gyroelongated triangular bicupola
(2 chiral forms)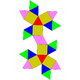
18 42 26 20 6 D3 45 Gyroelongated square bicupola
(2 chiral forms)
24 56 34 24 10 D4 46 Gyroelongated pentagonal bicupola
(2 chiral forms)
30 70 42 30 10 2 D5 47 Gyroelongated pentagonal cupolarotunda
(2 chiral forms)
35 80 47 35 5 7 C5 48 Gyroelongated pentagonal birotunda
(2 chiral forms)
40 90 52 40 12 D5 49 Augmented triangular prism 
7 13 8 6 2 C2v 50 Biaugmented triangular prism 
8 17 11 10 1 C2v 51 Triaugmented triangular prism 
9 21 14 14 D3h 52 Augmented pentagonal prism 
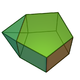
11 19 10 4 4 2 C2v 53 Biaugmented pentagonal prism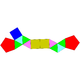 
12 23 13 8 3 2 C2v 54 Augmented hexagonal prism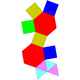 
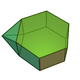
13 22 11 4 5 2 C2v 55 Parabiaugmented hexagonal prism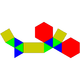 
14 26 14 8 4 2 D2h 56 Metabiaugmented hexagonal prism 
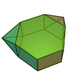
14 26 14 8 4 2 C2v 57 Triaugmented hexagonal prism 
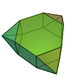
15 30 17 12 3 2 D3h 58 Augmented dodecahedron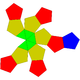 
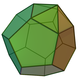
21 35 16 5 11 C5v 59 Parabiaugmented dodecahedron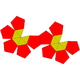 
22 40 20 10 10 D5d 60 Metabiaugmented dodecahedron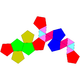 
22 40 20 10 10 C2v 61 Triaugmented dodecahedron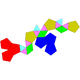 
23 45 24 15 9 C3v 62 Metabidiminished icosahedron 
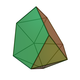
10 20 12 10 2 C2v 63 Tridiminished icosahedron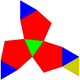 
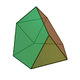
9 15 8 5 3 C3v 64 Augmented tridiminished icosahedron 
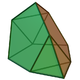
10 18 10 7 3 C3v 65 Augmented truncated tetrahedron 
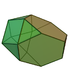
15 27 14 8 3 3 C3v 66 Augmented truncated cube 
28 48 22 12 5 5 C4v 67 Biaugmented truncated cube 
32 60 30 16 10 4 D4h 68 Augmented truncated dodecahedron 
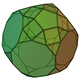
65 105 42 25 5 1 11 C5v 69 Parabiaugmented truncated dodecahedron 
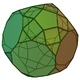
70 120 52 30 10 2 10 D5d 70 Metabiaugmented truncated dodecahedron 
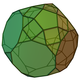
70 120 52 30 10 2 10 C2v 71 Triaugmented truncated dodecahedron 
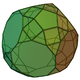
75 135 62 35 15 3 9 C3v 72 Gyrate rhombicosidodecahedron 
60 120 62 20 30 12 C5v 73 Parabigyrate rhombicosidodecahedron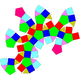 
60 120 62 20 30 12 D5d 74 Metabigyrate rhombicosidodecahedron 
60 120 62 20 30 12 C2v 75 Trigyrate rhombicosidodecahedron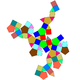 
60 120 62 20 30 12 C3v 76 Diminished rhombicosidodecahedron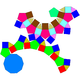 
55 105 52 15 25 11 1 C5v 77 Paragyrate diminished rhombicosidodecahedron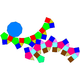 
55 105 52 15 25 11 1 C5v 78 Metagyrate diminished rhombicosidodecahedron 
55 105 52 15 25 11 1 Cs 79 Bigyrate diminished rhombicosidodecahedron 
55 105 52 15 25 11 1 Cs 80 Parabidiminished rhombicosidodecahedron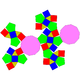 
50 90 42 10 20 10 2 D5d 81 Metabidiminished rhombicosidodecahedron 
50 90 42 10 20 10 2 C2v 82 Gyrate bidiminished rhombicosidodecahedron 
50 90 42 10 20 10 2 Cs 83 Tridiminished rhombicosidodecahedron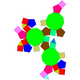 
45 75 32 5 15 9 3 C3v 84 Snub disphenoid
(Siamese dodecahedron)
8 18 12 12 D2d 85 Snub square antiprism 
16 40 26 24 2 D4d 86 Sphenocorona 
10 22 14 12 2 C2v 87 Augmented sphenocorona 
11 26 17 16 1 Cs 88 Sphenomegacorona 
12 28 18 16 2 C2v 89 Hebesphenomegacorona 
14 33 21 18 3 C2v 90 Disphenocingulum 
16 38 24 20 4 D2d 91 Bilunabirotunda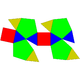 
14 26 14 8 2 4 D2h 92 Triangular hebesphenorotunda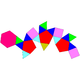 
18 36 20 13 3 3 1 C3v Legend:
- Jn – Johnson Solid Number
- Net – Flattened (unfolded) image
- V – Number of Vertices
- E – Number of Edges
- F – Number of Faces (total)
- F3 – Number of 3-sided Faces
- F4 – Number of 4-sided Faces
- F5 – Number of 5-sided Faces
- F6 – Number of 6-sided Faces
- F8 – Number of 8-sided Faces
- F10 – Number of 10-sided Faces
See also
- Near-miss Johnson solid
- Catalan solid
- Toroidal polyhedron
References
- Norman W. Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Contains the original enumeration of the 92 solids and the conjecture that there are no others.
- Victor A. Zalgaller (1969). Convex Polyhedra with Regular Faces. Consultants Bureau. No ISBN. The first proof that there are only 92 Johnson solids.
External links
- Sylvain Gagnon, "Convex polyhedra with regular faces", Structural Topology, No. 6, 1982, 83-95.
- Paper Models of Polyhedra Many links
- Johnson Solids by George W. Hart.
- Images of all 92 solids, categorized, on one page
- Weisstein, Eric W., "Johnson Solid" from MathWorld.
- VRML models of Johnson Solids by Jim McNeill
- VRML models of Johnson Solids by Vladimir Bulatov
Categories:- Johnson solids
Wikimedia Foundation. 2010.
