Truncated great icosahedron

Truncated great icosahedron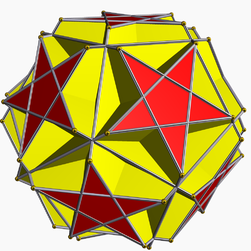
Type	Uniform star polyhedron
Elements	F = 32, E = 90 V = 60 (χ = 2)
Faces by sides	12{5/2}+20{6}
Wythoff symbol	2 5/2 | 3
Symmetry group	Ih, [5,3], *532
Index references	U55, C71, W95
6.6.5/2 (Vertex figure)	Great stellapentakis dodecahedron (dual polyhedron)

In geometry, the truncated great icosahedron is a nonconvex uniform polyhedron, indexed as U₅₅. It is given a Schläfli symbol t_0,1{3,5/2} as a truncated great icosahedron.

Cartesian coordinates

Cartesian coordinates for the vertices of a truncated great icosahedron centered at the origin are all the even permutations of

(±1, 0, ±3/τ)

(±2, ±1/τ, ±1/τ³)

(±(1+1/τ²), ±1, ±2/τ)

where τ = (1+√5)/2 is the golden ratio (sometimes written φ). Using 1/τ² = 1 − 1/τ one verifies that all vertices are on a sphere, centered at the origin, with the radius squared equal to 10−9/τ. The edges have length 2.

Related polyhedra

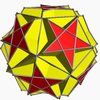
This polyhedron is the truncation of the great icosahedron:

The truncated great stellated dodecahedron is a degenerate polyhedron, with 20 triangular faces from the truncated vertices, and 12 (hidden) pentagonal faces as truncations of the original pentagram faces, the latter forming a great dodecahedron inscribed within and sharing the edges of the icosahedron.

Name	Great stellated dodecahedron	Truncated great stellated dodecahedron	Great icosidodecahedron	Truncated great icosahedron	Great icosahedron
Coxeter-Dynkin diagram
Picture

See also

• List of uniform polyhedra

External links

• Weisstein, Eric W., "Truncated great icosahedron" from MathWorld.

This polyhedron-related article is a stub. You can help Wikipedia by expanding it.v · Categories: Polyhedron stubs Uniform polyhedra Wikimedia Foundation. 2010. Игры ⚽ Нужно решить контрольную? Arthur Fremantle Great ditrigonal dodecicosidodecahedron Look at other dictionaries: Truncated great dodecahedron — Type Uniform star polyhedron Elements F = 24, E = 90 V = 60 (χ = −6) Faces by sides 12{5/2}+12{10} Wythof …   Wikipedia Truncated icosidodecahedron — (Click here for rotating model) Type Archimedean solid Uniform polyhedron Elements F = 62, E = 180, V = 120 (χ = 2) Faces by sides …   Wikipedia Truncated cuboctahedron — (Click here for rotating model) Type Archimedean solid Uniform polyhedron Elements F = 26, E = 72, V = 48 (χ = 2) Faces by sides …   Wikipedia Truncated octahedron — (Click here for rotating model) Type Archimedean solid Uniform polyhedron Elements F = 14, E = 36, V = 24 (χ = 2) Faces by sides 6 …   Wikipedia Nonconvex great rhombicosidodecahedron — Type Uniform star polyhedron Elements F = 62, E = 120 V = 60 (χ = 2) Faces by sides 20{3}+30{4}+12{5/2} …   Wikipedia Final stellation of the icosahedron — Two symmetric orthographic projections Symmetry group icosahedra …   Wikipedia Small triambic icosahedron — In geometry, the small triambic icosahedron is the dual to the uniform small ditrigonal icosidodecahedron. It is composed of 20 intersecting isogonal hexagon faces. It has 60 edges and 32 vertices, and Euler characteristic of −8.If the… …   Wikipedia Uniform star polyhedron — A display of uniform polyhedra at the Science Museum in London …   Wikipedia Kepler–Poinsot polyhedron — In geometry, a Kepler–Poinsot polyhedron is any of four regular star polyhedra. They may be obtained by stellating the regular convex dodecahedron and icosahedron, and differ from these in having regular pentagrammic faces or vertex figures.… …   Wikipedia List of mathematics articles (T) — NOTOC T T duality T group T group (mathematics) T integration T norm T norm fuzzy logics T schema T square (fractal) T symmetry T table T theory T.C. Mits T1 space Table of bases Table of Clebsch Gordan coefficients Table of divisors Table of Lie …   Wikipedia 18+ © Academic, 2000-2024 Contact us: Technical Support, Advertising Dictionaries export, created on PHP, Joomla, Drupal, WordPress, MODx. Mark and share Search through all dictionaries Translate… Search Internet Share the article and excerpts Direct link … Do a right-click on the link above and select “Copy Link”