Medial rhombic triacontahedron

Medial rhombic triacontahedron
Type	Star polyhedron
Elements	F = 30, E = 60 V = 24 (χ = −6)
Symmetry group	Ih, [5,3], *532
Index references	DU36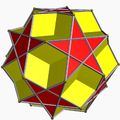
Dodecadodecahedron (dual polyhedron)

In geometry, the medial rhombic triacontahedron is a nonconvex isohedral polyhedron. It is the dual of the dodecadodecahedron. It has 30 intersecting rhombic faces.

It can also be called the small stellated triacontahedron.

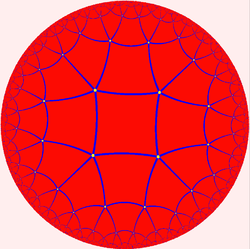
It is topologically equivalent to the hyperbolic order-5 square tiling, by distorting the rhombi into squares. As such, it is topologically a regular polyhedron of index two:^[1]

Note that the order-5 square tiling is dual to the order-4 pentagonal tiling, which is topologically equivalent to the dual of the medial rhombic triacontahedron, the dodecadodecahedron.

References

• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR730208 

1. ^ The Regular Polyhedra (of index two), David A. Richter

External links

• Weisstein, Eric W., "Medial Rhombic Triacontahedron" from MathWorld.
• Uniform polyhedra and duals

This polyhedron-related article is a stub. You can help Wikipedia by expanding it.v · Categories: Polyhedra Polyhedron stubs Wikimedia Foundation. 2010. Игры ⚽ Нужна курсовая? Medial pentagonal hexecontahedron Medial septal nucleus Look at other dictionaries: Medial deltoidal hexecontahedron — Type Star polyhedron Elements F = 60, E = 120 V = 54 (χ = −6) Symmetry group Ih, [5,3], *532 …   Wikipedia Medial pentagonal hexecontahedron — Type Star polyhedron Elements F = 60, E = 150 V = 84 (χ = −6) Symmetry group I, [5,3]+, 532 …   Wikipedia Dodecadodecahedron — Type Uniform star polyhedron Elements F = 24, E = 60 V = 30 (χ = −6) Faces by sides 12{5}+12{5/2} Wythoff symbol …   Wikipedia Snub dodecadodecahedron — Type Uniform star polyhedron Elements F = 84, E = 150 V = 60 (χ = −6) Faces by sides 60{3}+12{5}+12{5/2} Wythoff symbol …   Wikipedia Truncated great dodecahedron — Type Uniform star polyhedron Elements F = 24, E = 90 V = 60 (χ = −6) Faces by sides 12{5/2}+12{10} Wythof …   Wikipedia Truncated great icosahedron — Type Uniform star polyhedron Elements F = 32, E = 90 V = 60 (χ = 2) Faces by sides 12{5/2}+20{6} Wythoff symb …   Wikipedia Kepler–Poinsot polyhedron — In geometry, a Kepler–Poinsot polyhedron is any of four regular star polyhedra. They may be obtained by stellating the regular convex dodecahedron and icosahedron, and differ from these in having regular pentagrammic faces or vertex figures.… …   Wikipedia Nonconvex great rhombicosidodecahedron — Type Uniform star polyhedron Elements F = 62, E = 120 V = 60 (χ = 2) Faces by sides 20{3}+30{4}+12{5/2} …   Wikipedia Dodecadodecaedre — Dodécadodécaèdre Dodécadodécaèdre Type Polyèdre uniforme Éléments F=24, A=60, S=30 (χ= 6) Faces par cotés 12{5}+12{5/2} Configuration de sommet …   Wikipédia en Français Dodécadodécaèdre — Type Polyèdre uniforme Éléments F=24, A=60, S=30 (χ= 6) Faces par côtés 12{5}+12{5/2} Configuration de sommet …   Wikipédia en Français 18+ © Academic, 2000-2024 Contact us: Technical Support, Advertising Dictionaries export, created on PHP, Joomla, Drupal, WordPress, MODx. Mark and share Search through all dictionaries Translate… Search Internet Share the article and excerpts Direct link … Do a right-click on the link above and select “Copy Link”