Convex hull

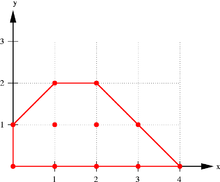
The convex hull of the red set is the blue convex set.

See also: Convex set and Convex combination

In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X.

The convex hull also has a linear-algebraic characterization: the convex hull of X is the set of all convex combinations of points in X.

In computational geometry, a basic problem is finding the convex hull for a given finite set of points in the plane.

Existence of the convex hull

To show that the convex hull of a set X in a real vector space V exists, notice that X is contained in at least one convex set (the whole space V, for example), and any intersection of convex sets containing X is also a convex set containing X. It is then clear that the convex hull is the intersection of all convex sets containing X. This can be used as an alternative definition of the convex hull.

The convex-hull operator Conv() has the characteristic properties of a hull operator:

extensive	S ⊆ Conv(S),
non-decreasing	S ⊆ T implies that Conv(S) ⊆ Conv(T), and
idempotent	Conv(Conv(S)) = Conv(S).

Thus, the convex-hull operator is a proper "hull" operator.

Algebraic characterization

Algebraically, the convex hull of X can be characterized as the set of all of the convex combinations of finite subsets of points from X: that is, the set of points of the form $\sum_{j=1}^n t_jx_j$, where n is an arbitrary natural number, the numbers t_j are non-negative and sum to 1, and the points x_j are in X. It is simple to check that this set satisfies either of the two definitions above. So the convex hull H_convex(X) of set X is:

$H_\mathrm{convex}(X) =\left\{\sum_{i=1}^k \alpha_i x_i \ \Bigg | \ x_i\in X, \, \alpha_i\in \mathbb{R}, \, \alpha_i \geq 0, \, \sum_{i=1}^k \alpha_i=1,\, k=1, 2, \dots\right\}.$

In fact, according to Carathéodory's theorem, if X is a subset of an N-dimensional vector space, convex combinations of at most N + 1 points are sufficient in the definition above. This is equivalent to saying that the convex hull of X is the union of all simplices with at most N+1 vertices from X.

The convex hull is defined for any kind of objects made up of points in a vector space, which may have any number of dimensions, including infinite-dimensional vector spaces. The convex hull of finite sets of points and other geometrical objects in a two-dimensional plane or three-dimensional space are special cases of practical importance.

Minkowski addition and convex hulls

See also: Minkowski addition and Shapley–Folkman lemma

Minkowski addition of sets. The sum of the squares Q₁=[0,1]² and Q₂=[1,2]² is the square Q₁+Q₂=[1,3]².

The operation of taking convex hulls behaves well with respect to the Minkowski addition of sets.

• In a real vector-space, the Minkowski sum of two (non-empty) sets S₁ and S₂ is defined to be the set S₁ + S₂ formed by the addition of vectors element-wise from the summand-sets

S₁ + S₂ = { x₁ + x₂ : x₁ ∈ S₁ and x₂ ∈ S₂ }.

More generally, the Minkowski sum of a finite family of (non-empty) sets S_n is the set formed by element-wise addition of vectors

∑ S_n = { ∑ x_n : x_n ∈ S_n }.

• For all subsets S₁ and S₂ of a real vector-space, the convex hull of their Minkowski sum is the Minkowski sum of their convex hulls

Conv( S₁ + S₂ ) = Conv( S₁ ) + Conv( S₂ ).

This result holds more generally for each finite collection of non-empty sets

Conv(  ∑ S_n  ) = ∑ Conv( S_n ).

In other words, the operations of Minkowski summation and of forming convex hulls are commuting operations.^[1][2]

These results show that Minkowski addition differs from the union operation of set theory; indeed, the union of two convex sets need not be convex: The inclusion Conv(S) ∪ Conv(T) ⊆ Conv(S ∪ T) is generally strict. The convex-hull operation is needed for the set of convex sets to form a lattice, in which the "join" operation is the convex hull of the union of two convex sets

Conv(S)∨Conv(T) = Conv( S ∪ T ) = Conv( Conv(S) ∪ Conv(T) ).

Convex hull of a finite point set

Convex hull of some points in the plane

The convex hull of a finite point set $P \in \mathbb{R}^n$ forms a convex polytope in $\mathbb{R}^n$. Each $p \in P$ such that $p \notin$ Conv(P \ {p}) is called a vertex of Conv(P). In fact, a convex polytope in $\mathbb{R}^n$ is the convex hull of its vertices.

If the points are all on a line, the convex hull is the line segment joining the outermost two points. In the planar case, the convex hull is a convex polygon unless all points are on the same line. Similarly, in three dimensions the convex hull is in general the minimal convex polyhedron that contains all the points in the set.

Convex hull of a finite set: elastic-band analogy

When the set X is a nonempty finite subset of the plane (that is, two-dimensional), we may imagine stretching a rubber band so that it surrounds the entire set X and then releasing it, allowing it to contract; when it becomes taut, it encloses the convex hull of X.^{[3] [4]}

Computation of convex hulls

Main article: Convex hull algorithms

In computational geometry, a number of algorithms are known for computing the convex hull for a finite set of points and for other geometric objects.

Computing the convex hull means constructing an unambiguous, efficient representation of the required convex shape. The complexity of the corresponding algorithms is usually estimated in terms of n, the number of input points, and h, the number of points on the convex hull.

Relations to other geometric structures

The Delaunay triangulation of a point set and its dual, the Voronoi Diagram, are mathematically related to convex hulls: the Delaunay triangulation of a point set in Rⁿ can be viewed as the projection of a convex hull in Rⁿ⁺¹.^[5]

Applications

The problem of finding convex hulls finds its practical applications in pattern recognition, image processing, statistics, GIS and static code analysis by abstract interpretation. It also serves as a tool, a building block for a number of other computational-geometric algorithms such as the rotating calipers method for computing the width and diameter of a point set.

See also

• Hull operator
• Affine hull
• Linear hull
• Krein–Milman theorem
• Choquet theory
• Holomorphically convex hull
• Orthogonal convex hull
• Oloid
• Carathéodory's theorem
• Helly's theorem
• Shapley–Folkman lemma

References

1. ^ Theorem 3 (pages 562–563): Krein, M.; Šmulian, V. (1940). "On regularly convex sets in the space conjugate to a Banach space". Annals of Mathematics (2), Second series 41: pp. 556–583. doi:10.2307/1968735. JSTOR 1968735. MR2009. 
2. ^ For the commutativity of Minkowski addition and convexification, see Theorem 1.1.2 (pages 2–3) in Schneider; this reference discusses much of the literature on the convex hulls of Minkowski sumsets in its "Chapter 3 Minkowski addition" (pages 126–196): Schneider, Rolf (1993). Convex bodies: The Brunn–Minkowski theory. Encyclopedia of mathematics and its applications. 44. Cambridge: Cambridge University Press. pp. xiv+490. ISBN 0-521-35220-7. MR1216521. 
3. ^ Pages 195–196: Evar D. Nering and Albert W. Tucker, 1993, Linear Programs and Related Problems, Academic Press.
4. ^ Knuth, Donald E. (1992), Axioms and hulls, Lecture Notes in Computer Science, 606, Heidelberg: Springer-Verlag, pp. ix+109, doi:10.1007/3-540-55611-7, ISBN 3-540-55611-7, MR1226891, http://www-cs-faculty.stanford.edu/~uno/aah.html, retrieved 5 May 2011 
5. ^ Brown, K. Q. (1979). "Voronoi diagrams from convex hulls". Information Processing Letters 9 (5): 223–228. doi:10.1016/0020-0190(79)90074-7. 

• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 33.3: Finding the convex hull, pp. 947–957.

• Franco P. Preparata, S.J. Hong. Convex Hulls of Finite Sets of Points in Two and Three Dimensions, Commun. ACM, vol. 20, no. 2, pp. 87–93, 1977.

• M. de Berg; M. van Kreveld; Mark Overmars; O. Schwarzkopf. (2000). Computational Geometry, Algorithms and Applications. Springer. 

External links

• Weisstein, Eric W., "Convex Hull" from MathWorld.
• "Convex Hull" by Eric W. Weisstein, Wolfram Demonstrations Project, 2007.