Convex set

A convex set.

A non-convex set, with a line-segment outside the set.

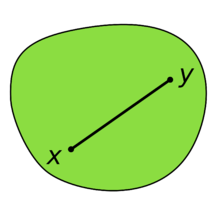
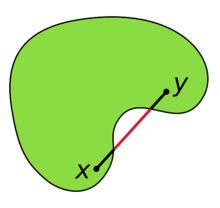
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object. For example, a solid cube is convex, but anything that is hollow or has a dent in it, for example, a crescent shape, is not convex.

The notion can be generalized to other spaces as described below.

In vector spaces

A function is convex if and only if its epigraph, the region (in green) above its graph (in blue), is a convex set.

Let S be a vector space over the real numbers, or, more generally, some ordered field. This includes Euclidean spaces. A set C in S is said to be convex if, for all x and y in C and all t in the interval [0,1], the point

(1 − t ) x + t y

is in C. In other words, every point on the line segment connecting x and y is in C. This implies that a convex set in a real or complex topological vector space is path-connected, thus connected.

A set C is called absolutely convex if it is convex and balanced.

The convex subsets of R (the set of real numbers) are simply the intervals of R. Some examples of convex subsets of Euclidean 2-space are regular polygons and bodies of constant width. Some examples of convex subsets of Euclidean 3-space are the Archimedean solids and the Platonic solids. The Kepler-Poinsot polyhedra are examples of non-convex sets.

Properties

If S is a convex set, for any $u_1,u_2,\ldots,u_r$ in S, and any nonnegative numbers $\lambda_1,\lambda_2,\ldots,\lambda_r$ such that $\lambda_1+\lambda_2+\cdots+\lambda_r=1$, then the vector $\sum_{k=1}^r\lambda_k u_k$ is in S. A vector of this type is known as a convex combination of $u_1,u_2,\ldots,u_r$.

Intersections and unions

The collection of convex subsets of a vector space has the following properties:^[1][2]

1. The empty set and the whole vector-space are convex.
2. The intersection of any collection of convex sets is convex.
3. The union of a non-decreasing sequence of convex subsets is a convex set.

For the preceding property of unions of non-decreasing sequences of convex sets, the restriction to nested sets was important: The union of two convex sets need not be convex.

Convex hulls

Every subset A of the vector space is contained within a smallest convex set (called the convex hull of A), namely the intersection of all convex sets containing A. The convex-hull operator Conv() has the characteristic properties of a hull operator:

extensive	S ⊆ Conv(S),
non-decreasing	S ⊆ T implies that Conv(S) ⊆ Conv(T), and
idempotent	Conv(Conv(S)) = Conv(S).

The convex-hull operation is needed for the set of convex sets to form a lattice, in which the "join" operation is the convex hull of the union of two convex sets

Conv(S)∨Conv(T) = Conv( S ∪ T ) = Conv( Conv(S) ∪ Conv(T) ).

The intersection of any collection of convex sets is itself convex, so the convex subsets of a (real or complex) vector space form a complete lattice.

Minkowski addition

Main article: Minkowski addition

Minkowski addition of sets. The sum of the squares Q₁=[0,1]² and Q₂=[1,2]² is the square Q₁+Q₂=[1,3]².

• In a real vector-space, the Minkowski sum of two (non-empty) sets S₁ and S₂ is defined to be the set S₁ + S₂ formed by the addition of vectors element-wise from the summand-sets

S₁ + S₂ = { x₁ + x₂ : x₁ ∈ S₁ and x₂ ∈ S₂ }.

More generally, the Minkowski sum of a finite family of (non-empty) sets S_n is the set formed by element-wise addition of vectors

∑ S_n = { ∑ x_n : x_n ∈ S_n }.

For Minkowski addition, the zero set {0} containing only the zero vector 0 has special importance: For every non-empty subset S of a vector space

S + {0} = S;

in algebraic terminology, the zero vector 0 is the identity element of Minkowski addition (on the collection of non-empty sets).^[3]

Convex hulls of Minkowski sums

Minkowski addition behaves well with respect to the operation of taking convex hulls, as shown by the following proposition:

• For all subsets S₁ and S₂ of a real vector-space, the convex hull of their Minkowski sum is the Minkowski sum of their convex hulls

Conv( S₁ + S₂ ) = Conv( S₁ ) + Conv( S₂ ).

This result holds more generally for each finite collection of non-empty sets

Conv(  ∑ S_n  ) = ∑ Conv( S_n ).

In mathematical terminology, the operations of Minkowski summation and of forming convex hulls are commuting operations.^[4][5]

Closed convex sets

Closed convex sets can be characterised as the intersections of closed half-spaces (sets of point in space that lie on and to one side of a hyperplane). From what has just been said, it is clear that such intersections are convex, and they will also be closed sets. To prove the converse, i.e., every convex set may be represented as such intersection, one needs the supporting hyperplane theorem in the form that for a given closed convex set C and point P outside it, there is a closed half-space H that contains C and not P. The supporting hyperplane theorem is a special case of the Hahn–Banach theorem of functional analysis.

The Minkowski sum of two compact convex sets is closed, as is the sum of a compact convex set and a closed convex set.^[6]

Generalizations and extensions for convexity

The notion of convexity in the Euclidean space may be generalized by modifying the definition in some or other aspects. The common name "generalized convexity" is used, because the resulting objects retain certain properties of convex sets.

Star-convex sets

Main article: Star domain

Let C be a set in a real or complex vector space. C is star convex if there exists an x₀ in C such that the line segment from x₀ to any point y in C is contained in C. Hence a non-empty convex set is always star-convex but a star-convex set is not always convex.

Orthogonal convexity

Main article: Orthogonal convex hull

An example of generalized convexity is orthogonal convexity.^[7]

A set S in the Euclidean space is called orthogonally convex or ortho-convex, if any segment parallel to any of the coordinate axes connecting two points of S lies totally within S. It is easy to prove that an intersection of any collection of orthoconvex sets is orthoconvex. Some other properties of convex sets are valid as well.

Not Euclidean geometry

The definition of a convex set and a convex hull extends naturally to geometries which are not Euclidean by defining a geodesically convex set to be one that contains the geodesics joining any two points in the set.

Order topology

Convexity can be extended for a space X endowed with the order topology, using the total order < of the space.^[8]

Let $Y\subseteq X$. The subspace Y is a convex set if for each pair of points $a,b\in Y$ such that a < b, the interval $\left( a,b \right) = \left\{ x \in X:a<x<b \right\}$ is contained in Y. That is, Y is convex if and only if $\forall a,b\in Y, a<b \Rightarrow \left(a,b\right)\subseteq Y$.

Convexity spaces

The notion of convexity may be generalised to other objects, if certain properties of convexity are selected as axioms.

Given a set X, a convexity over X is a collection $\mathcal{C}$ of subsets of X satisfying the following axioms:^[1][2]

1. The empty set and X are in $\mathcal{C}$
2. The intersection of any collection from $\mathcal{C}$ is in $\mathcal{C}$.
3. The union of a chain (with respect to the inclusion relation) of elements of $\mathcal{C}$ is in $\mathcal{C}$.

The elements of $\mathcal{C}$ are called convex sets and the pair (X, $\mathcal{C}$) is called a convexity space. For the ordinary convexity, the first two axioms hold, and the third one is trivial.

For an alternative definition of abstract convexity, more suited to discrete geometry, see the convex geometries associated with antimatroids.

See also

• Convex function
• Holomorphically convex hull
• Pseudoconvexity
• Convex metric space
• Concave set
• Helly's theorem
• Carathéodory's theorem (convex hull)
• Choquet theory
• Shapley–Folkman lemma

References

1. ^ ^{a b} Soltan, Valeriu, Introduction to the Axiomatic Theory of Convexity, Ştiinţa, Chişinău, 1984 (in Russian).
2. ^ ^{a b} Singer, Ivan (1997). Abstract convex analysis. Canadian Mathematical Society series of monographs and advanced texts. New York: John Wiley & Sons, Inc.. pp. xxii+491. ISBN 0-471-16015-6. MR1461544. 
3. ^ The empty set is important in Minkowski addition, because the empty set annihilates every other subset: For every subset S of a vector space, its sum with the empty set is empty

   S+∅ = ∅.

4. ^ Theorem 3 (pages 562–563): Krein, M.; Šmulian, V. (1940). "On regularly convex sets in the space conjugate to a Banach space". Annals of Mathematics (2), Second series 41: pp. 556–583. doi:10.2307/1968735. JSTOR 1968735. 
5. ^ For the commutativity of Minkowski addition and convexification, see Theorem 1.1.2 (pages 2–3) in Schneider; this reference discusses much of the literature on the convex hulls of Minkowski sumsets in its "Chapter 3 Minkowski addition" (pages 126–196): Schneider, Rolf (1993). Convex bodies: The Brunn–Minkowski theory. Encyclopedia of mathematics and its applications. 44. Cambridge: Cambridge University Press. pp. xiv+490. ISBN 0-521-35220-7. MR1216521. 
6. ^ R. T. Rockafellar, Convex analysis, Princeton University Press, Princeton, NJ, 1970. Reprint: 1997.
7. ^ Rawlins G.J.E. and Wood D, "Ortho-convexity and its generalizations", in: Computational Morphology, 137-152. Elsevier, 1988.
8. ^ Munkres, James; Topology, Prentice Hall; 2nd edition (December 28, 1999). ISBN 0-13-181629-2.

External links

• Lectures on Convex Sets, notes by Niels Lauritzen, at Aarhus University, March 2010.