Curve of constant width

A Reuleaux triangle is a curve of constant width. The sides of the square are supporting lines: each touches the curve but does not intersect the interior. The Reuleaux triangle can be rotated whilst always touching each side of the square in a single point; this demonstrates that its width (separation between parallel supporting lines) is constant in all directions.

Construction diagram for generating a curve of constant width from a triangle

In geometry, a curve of constant width is a convex planar shape whose width, defined as the perpendicular distance between two distinct parallel lines each intersecting its boundary in a single point, is the same regardless of the direction of those two parallel lines.

More generally, any compact convex planar body D has one pair of parallel supporting lines in any given direction. A supporting line is a line that has at least one point in common with the boundary of D but no points in common with the interior of D. The width of the body is defined as before. If the width of D is the same in all directions, the body is said to have constant width and its boundary is a curve of constant width; the planar body itself is called an orbiform.

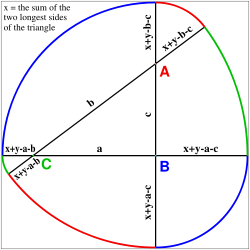
The width of a circle is constant: its diameter. The width of a square varies between the length of a side and that of a diagonal, in the ratio 1:√2. Thus the question arises: if a given shape's width is constant in all directions, is it necessarily a circle? The surprising answer is that there are many non-circular shapes of constant width. A nontrivial example is the Reuleaux triangle. To construct this, take an equilateral triangle with vertices ABC and draw the arc BC on the circle centered at A, the arc CA on the circle centered at B, and the arc AB on the circle centered at C. The resulting figure is of constant width.

The Reuleaux triangle lacks tangent continuity at three points, but constant-width curves can also be constructed without such discontinuities^[1] (as shown in the second illustration at right). Curves of constant width can be generated by joining circular arcs centered on the vertices of a regular or irregular convex polygon with an odd number of sides (triangle, pentagon, heptagon, etc.).^[2]

Properties

Curves of constant width can be rotated between parallel line segments. To see this, simply note that one can rotate parallel line segments (supporting lines) around curves of constant width by definition. Consequently, a curve of constant width can be rotated in a square.

A basic result on curves of constant width is Barbier's theorem, which asserts that the perimeter of any curve of constant width is equal to the width (diameter) multiplied by π. A simple example of this would be a circle with width (diameter) d having a perimeter of πd.

By the isoperimetric inequality and Barbier's theorem, the circle has the maximum area of any curve of given constant width. The Blaschke-Lebesgue theorem says that the Reuleaux triangle has the least area of any curve of given constant width.

Applications

Rollers

A wheel rotating around a fixed axle must be circular in shape to allow smooth forward motion; however, a loose "roller" does not have to be circular in shape to allow smooth forward motion (without any vertical bumpiness) — any curve of constant width will do. Therefore if flat material is placed on two or more rollers (in the shape of curves of the same constant width) resting on a flat surface, the material will remain a constant height off the ground as it is pushed forward (though the rollers themselves will appear to "move in a curiously irregular manner" if their shape is significantly non-circular).^[3]

Curves of constant width are also the general answer to a brain teaser: "What shape can you make a manhole cover so that it cannot fall down through the hole?" In practice, there is no compelling reason to make manhole covers non-circular. Circles are easier to machine, and need not be rotated to a particular alignment in order to seal the hole.

Generalizations

Δ curves, which can be rotated in the equilateral triangle, have many similar properties to curves of constant width.

The generalization of the definition of bodies of constant width to convex bodies in R³ and their boundaries leads to the concept of surface of constant width (in the case of a Reuleaux triangle, this does not lead to a Reuleaux tetrahedron, but to Meissner bodies). There is also the concept of space curves of constant width, whose widths are defined by tangent planes.

Examples

Famous examples of a curve of constant width are the British 20p and 50p coins. Their heptagonal shape with curved sides means that the currency detector in an automated coin machine will always measure the same width, no matter which angle it takes its measurement from.

There exists a polynomial f(x,y) of degree 8, whose graph (i.e., set of points in R² for which f(x,y) = 0) is a non-circular curve of constant width.[1]

References

1. ^ Mathematical Models by H. Martyn Cundy and A.P. Rollett, second edition, 1961 (Oxford University Press), p. 211.
2. ^ Mathematical Models by H. Martyn Cundy and A.P. Rollett, second edition, 1961 (Oxford University Press), p. 212.
3. ^ Mathematical Models by H. Martyn Cundy and A.P. Rollett, second edition, 1961 (Oxford University Press), pp. 210-212.

External links

• How round is your circle? contains a chapter on this topic.
• Animated Java applet by Michael Borcherds showing an irregular shape of constant width (that you can change) made using GeoGebra.
• Star Construction of Shapes of Constant Width at cut-the-knot
• Weisstein, Eric W. "Curve of Constant Width." From MathWorld--A Wolfram Web Resource.
• Multi-angle-wheel bicycle appears in Qingdao - bicycle with wheels using this property.