Oloid

Oloid
Oloid
Paper Oloid
Oloid

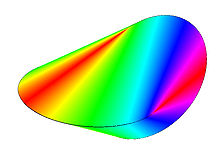
An oloid is a geometric object that was discovered by Paul Schatz (1898–1979) in 1929. It is formed by taking the convex hull of the shape made by intersecting two disks of equal radius at right angles within one another, with the distance between the centers of the disks equal to their radius. The resulting convex hull is an oloid.

While rolling, the distance between center of gravity and floor has two minimums and maximums, so it rolls very swinging but smooth: it never falls over its edges. It is the only known object other than some members of the sphericon family that develops its entire surface while rolling. The surface of an oloid with circles of radius r is 4πr 2, which is also the surface of a sphere with that radius. The volume of an oloid is approximately 3.0524r3.

Schatz discovered in 1929 that the Platonic solids could be inverted, and one of the products of the inversion of the cube was the oloid. Based on two circles set perpendicular to each other, it rolls in a straight line such that its whole surface touches the plane on which it is rolled. The oloid visually resembles a Möbius strip. Schatz came to his geometric insights by studying the work of Rudolf Steiner, the founder of anthroposophy. Schatz obtained Swiss Patent no 500000 for his oloid mixer. Development has since continued, and the oloid is applied in ever more numerous ways.[citation needed]

Another object is defined, when the distance of the intersecting disks is √2 times their radius. This is often called "Two circle roller". It is not solid as the oloid, it consists just of the two disks. It is interesting, because its center of gravity has a constant distance to floor, thus it rolls smoothly but straightforward, not as swinging as the oloid, with which it is sometimes confused.

References

External links



Stub icon This geometry-related article is a stub. You can help Wikipedia by expanding it.