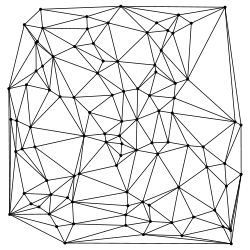
Delaunay triangulation

A Delaunay triangulation in the plane with circumcircles shown

In mathematics and computational geometry, a Delaunay triangulation for a set P of points in the plane is a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P). Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the triangulation; they tend to avoid skinny triangles. The triangulation was invented by Boris Delaunay in 1934.^[1]

For a set of points on the same line there is no Delaunay triangulation (the notion of triangulation is degenerate for this case). For four or more points on the same circle (e.g., the vertices of a rectangle) the Delaunay triangulation is not unique: each of the two possible triangulations that split the quadrangle into two triangles satisfies the "Delaunay condition", i.e., the requirement that the circumcircles of all triangles have empty interiors.

By considering circumscribed spheres, the notion of Delaunay triangulation extends to three and higher dimensions. Generalizations are possible to metrics other than Euclidean. However in these cases a Delaunay triangulation is not guaranteed to exist or be unique.

Relationship with the Voronoi diagram

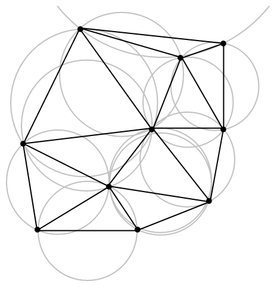
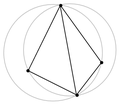
The Delaunay triangulation of a discrete point set P in general position corresponds to the dual graph of the Voronoi tessellation for P. Special cases include the existence of three points on a line and four points on circle.

• 

  The Delaunay triangulation with all the circumcircles and their centers (in red).

• 

  Connecting the centers of the circumcircles produces the Voronoi diagram (in red).

d-dimensional Delaunay

For a set P of points in the (d-dimensional) Euclidean space, a Delaunay triangulation is a triangulation DT(P) such that no point in P is inside the circum-hypersphere of any simplex in DT(P). It is known^[2] that there exists a unique Delaunay triangulation for P, if P is a set of points in general position; that is, there exists no k-flat containing k + 2 points nor a k-sphere containing k + 3 points, for 1 ≤ k ≤ d − 1 (e.g., for a set of points in ℝ³; no three points are on a line, no four on a plane, no four are on a circle, and no five on a sphere).

The problem of finding the Delaunay triangulation of a set of points in d-dimensional Euclidean space can be converted to the problem of finding the convex hull of a set of points in (d + 1)-dimensional space, by giving each point p an extra coordinate equal to |p|², taking the bottom side of the convex hull, and mapping back to d-dimensional space by deleting the last coordinate. As the convex hull is unique, so is the triangulation, assuming all facets of the convex hull are simplices. Nonsimplicial facets only occur when d + 2 of the original points lie on the same d-hypersphere, i.e., the points are not in general position.

Properties

Let n be the number of points and d the number of dimensions.

• The union of all simplices in the triangulation is the convex hull of the points.
• The Delaunay triangulation contains O(n^{⌈d / 2⌉}) simplices.^[3]
• In the plane (d = 2), if there are b vertices on the convex hull, then any triangulation of the points has at most 2n − 2 − b triangles, plus one exterior face (see Euler characteristic).
• In the plane, each vertex has on average six surrounding triangles.
• In the plane, the Delaunay triangulation maximizes the minimum angle. Compared to any other triangulation of the points, the smallest angle in the Delaunay triangulation is at least as large as the smallest angle in any other. However, the Delaunay triangulation does not necessarily minimize the maximum angle.
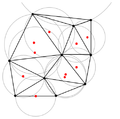
• A circle circumscribing any Delaunay triangle does not contain any other input points in its interior.
• If a circle passing through two of the input points doesn't contain any other of them in its interior, then the segment connecting the two points is an edge of a Delaunay triangulation of the given points.
• The Delaunay triangulation of a set of points in d-dimensional spaces is the projection of the points of convex hull onto a (d + 1)-dimensional paraboloid.
• The closest neighbor b to any point p is on an edge bp in the Delaunay triangulation since the nearest neighbor graph is a subgraph of the Delaunay triangulation.

Visual Delaunay definition: Flipping

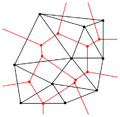
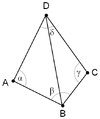
From the above properties an important feature arises: Looking at two triangles ABD and BCD with the common edge BD (see figures), if the sum of the angles α and γ is less than or equal to 180°, the triangles meet the Delaunay condition.

This is an important property because it allows the use of a flipping technique. If two triangles do not meet the Delaunay condition, switching the common edge BD for the common edge AC produces two triangles that do meet the Delaunay condition:

• 

  This triangulation does not meet the Delaunay condition (the sum of α and γ is bigger than 180°).

• 

  This triangulation does not meet the Delaunay condition (the circumcircles contain more than 3 points).

• 

  Flipping the common edge produces a Delaunay triangulation for the four points.

Algorithms

Many algorithms for computing Delaunay triangulations rely on fast operations for detecting when a point is within a triangle's circumcircle and an efficient data structure for storing triangles and edges. In two dimensions, one way to detect if point D lies in the circumcircle of A, B, C is to evaluate the determinant:^[4]

$\begin{vmatrix} A_x & A_y, & A_x^2 + A_y^2, & 1\\[6pt] B_x & B_y, & B_x^2 + B_y^2, & 1\\[6pt] C_x & C_y, & C_x^2 + C_y^2, & 1\\[6pt] D_x & D_y, & D_x^2 + D_y^2, & 1 \end{vmatrix} = \begin{vmatrix} A_x - D_x, & A_y - D_y, & (A_x^2 - D_x^2) + (A_y^2 - D_y^2) \\[6pt] B_x - D_x, & B_y - D_y, & (B_x^2 - D_x^2) + (B_y^2 - D_y^2) \\[6pt] C_x - D_x, & C_y - D_y, & (C_x^2 - D_x^2) + (C_y^2 - D_y^2) \\[6pt] \end{vmatrix} > 0$

When A, B and C are sorted in a counterclockwise order, this determinant is positive if and only if D lies inside the circumcircle.

Flip algorithms

As mentioned above, if a triangle is non-Delaunay, we can flip one of its edges. This leads to a straightforward algorithm: construct any triangulation of the points, and then flip edges until no triangle is non-Delaunay. Unfortunately, this can take O(n²) edge flips, and does not extend to three dimensions or higher.^[2]

Incremental

The most straightforward way of efficiently computing the Delaunay triangulation is to repeatedly add one vertex at a time, retriangulating the affected parts of the graph. When a vertex v is added, we split in three the triangle that contains v, then we apply the flip algorithm. Done naively, this will take O(n) time: we search through all the triangles to find the one that contains v, then we potentially flip away every triangle. Then the overall runtime is O(n²).

If we insert vertices in random order, it turns out (by a somewhat intricate proof) that each insertion will flip, on average, only O(1) triangles – although sometimes it will flip many more.^[5] This still leaves the point location time to improve. We can store the history of the splits and flips performed: each triangle stores a pointer to the two or three triangles that replaced it. To find the triangle that contains v, we start at a root triangle, and follow the pointer that points to a triangle that contains v, until we find a triangle that has not yet been replaced. On average, this will also take O(log n) time. Over all vertices, then, this takes O(n log n) time.^[2] While the technique extends to higher dimension (as proved by Edelsbrunner and Shah^[6]), the runtime can be exponential in the dimension even if the final Delaunay triangulation is small.

The Bowyer–Watson algorithm provides another approach for incremental construction. It gives an alternative to edge flipping for computing the Delaunay triangles containing a newly inserted vertex.

Divide and conquer

A divide and conquer algorithm for triangulations in two dimensions is due to Lee and Schachter which was improved by Guibas and Stolfi^[7] and later by Dwyer. In this algorithm, one recursively draws a line to split the vertices into two sets. The Delaunay triangulation is computed for each set, and then the two sets are merged along the splitting line. Using some clever tricks, the merge operation can be done in time O(n), so the total running time is O(n log n).^[8]

For certain types of point sets, such as a uniform random distribution, by intelligently picking the splitting lines the expected time can be reduced to O(n log log n) while still maintaining worst-case performance.

A divide and conquer paradigm to performing a triangulation in d dimensions is presented in "DeWall: A fast divide and conquer Delaunay triangulation algorithm in E^d" by P. Cignoni, C. Montani, R. Scopigno.^[9]

Divide and conquer has been shown to be the fastest DT generation technique.^[10][11]

Sweepline

Fortune's Algorithm uses a sweepline technique to achieve O(n log n) runtime in the planar case.

Sweephull

Sweephull^[12] is a fast hybrid technique for 2D Delaunay triangulation that uses a radially propagating sweep-hull (sequentially created from the radially sorted set of 2D points, giving a non-overlapping triangulation), paired with a final iterative triangle flipping step. Empirical results indicate the algorithm runs in approximately half the time of Qhull, and free implementations in C++ and C# are available.^[13]

Applications

The Euclidean minimum spanning tree of a set of points is a subset of the Delaunay triangulation of the same points, and this can be exploited to compute it efficiently.

For modelling terrain or other objects given a set of sample points, the Delaunay triangulation gives a nice set of triangles to use as polygons in the model. In particular, the Delaunay triangulation avoids narrow triangles (as they have large circumcircles compared to their area). See triangulated irregular network.

Delaunay triangulations can be used to determine the density or intensity of points samplings by means of the DTFE.

The Delaunay triangulation of a random set of 100 points in a plane.

Delaunay triangulations are often used to build meshes for space-discretised solvers such as the finite element method and the finite volume method of physics simulation, because of the angle guarantee and because fast triangulation algorithms have been developed. Typically, the domain to be meshed is specified as a coarse simplicial complex; for the mesh to be numerically stable, it must be refined, for instance by using Ruppert's algorithm.

See also

• Beta skeleton
• Constrained Delaunay triangulation
• Delaunay tessellation field estimator
• Gabriel graph
• Gradient pattern analysis
• Pitteway triangulation
• Urquhart graph
• Voronoi diagram

References

1. ^ B. Delaunay: Sur la sphère vide, Izvestia Akademii Nauk SSSR, Otdelenie Matematicheskikh i Estestvennykh Nauk, 7:793–800, 1934
2. ^ ^{a b c} de Berg, Mark; Otfried Cheong, Marc van Kreveld, Mark Overmars (2008). Computational Geometry: Algorithms and Applications. Springer-Verlag. ISBN 978-3-540-77973-5. http://www.cs.uu.nl/geobook/interpolation.pdf. 
3. ^ Seidel, R. (1995). "The upper bound theorem for polytopes: an easy proof of its asymptotic version". Computational Geometry 5 (2): 115–116. doi:10.1016/0925-7721(95)00013-Y. http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6TYS-3YVD096-C&_user=108429&_coverDate=09%2F30%2F1995&_rdoc=1&_fmt=high&_orig=search&_origin=search&_sort=d&_docanchor=&view=c&_acct=C000059713&_version=1&_urlVersion=0&_userid=108429&md5=70a4159a39ed8ab2c6709025aa77d5de&searchtype=a. 
4. ^ Guibas, Lenoidas; Stolfi, Jorge (1985-04-01). "Primitives for the manipulation of general subdivisions and the computation of Voronoi". ACM. p. 107. http://portal.acm.org/citation.cfm?id=282923. Retrieved 2009-08-01. 
5. ^ Guibas, L.; D. Knuth; M. Sharir (1992). "Randomized incremental construction of Delaunay and Voronoi diagrams". Algorithmica 7: 381–413. doi:10.1007/BF01758770. http://www.springerlink.com/content/p8377h68j82l6860. 
6. ^ Edelsbrunner, Herbert; Nimish Shah (1996). "Incremental Topological Flipping Works for Regular Triangulations". Algorithmica 15 (3): 223–241. doi:10.1007/BF01975867. http://www.springerlink.com/content/4gdja72vx1qmg44x/?p=a74909a339d9498cbff326f08b084b4c&pi=1. 
7. ^ Computing Constrained Delaunay Triangulations
8. ^ G. Leach: Improving Worst-Case Optimal Delaunay Triangulation Algorithms. June 1992
9. ^ Cignoni, P.; C. Montani; R. Scopigno (1998). "DeWall: A fast divide and conquer Delaunay triangulation algorithm in E^d". Computer-Aided Design 30 (5): 333–341. doi:10.1016/S0010-4485(97)00082-1. 
10. ^ A Comparison of Sequential Delaunay Triangulation Algorithms http://www.cs.berkeley.edu/~jrs/meshpapers/SuDrysdale.pdf
11. ^ http://www.cs.cmu.edu/~quake/tripaper/triangle2.html
12. ^ S-hull
13. ^ http://www.s-hull.org/

External links

• Delaunay triangulation in CGAL, the Computational Geometry Algorithms Library:
  • Yvinec, Mariette. "2D Triangulation". http://www.cgal.org/Pkg/Triangulation2. Retrieved April 2010. 
  • Pion, Sylvain; Teillaud, Monique. "3D Triangulations". http://www.cgal.org/Pkg/Triangulation3. Retrieved April 2010. 
  • Hert, Susan; Seel, Michael. "dD Convex Hulls and Delaunay Triangulations". http://www.cgal.org/Pkg/ConvexHullD. Retrieved April 2010. 
• "Delaunay triangulation". Wolfram MathWorld. http://mathworld.wolfram.com/DelaunayTriangulation.html. Retrieved April 2010. 
• "Qhull". http://www.qhull.org. Retrieved April 2010.  — Code for Convex Hull, Delaunay Triangulation, Voronoi Diagram, and Halfspace Intersection
• Shewchuk, Jonathan Richard. "Triangle". http://www.cs.cmu.edu/~quake/triangle.html. Retrieved April 2010.  – A Two-Dimensional Quality Mesh Generator and Delaunay Triangulator
• Kumar, Piyush; Mohanty, Somya. "Triangle++". http://www.compgeom.com/~piyush/scripts/triangle/.  – A C++ wrapper on Triangle
• "Poly2Tri". Google Code. http://code.google.com/p/poly2tri/. Retrieved April 2010.  – A sweepline Constrained Delaunay Triangulation (CDT) library, available in ActionScript 3, C, C++, C#, Go, Java, Javascript, Python and Ruby