Dual graph

G′ is the dual graph of G

In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual of G, then G is a dual of H (if G is connected). The same notion of duality may also be used for more general embeddings of graphs on manifolds.

Properties

• The dual of a planar graph is a planar multigraph - multiple edges.^[1]
• If G is a connected graph and if G′ is a dual of G then G is a dual of G′.

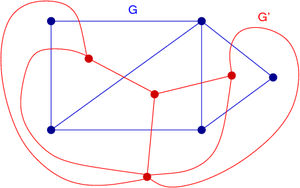
Two red graphs are duals for the blue one, but they are not isomorphic.

• Dual graphs are not unique, in the sense that the same graph can have non-isomorphic dual graphs because the dual graph depends on a particular plane embedding. In the picture, red graphs are not isomorphic because the upper one has a vertex with degree 6 (the outer region).

Because of the dualism, any result involving counting regions and vertices can be dualized by exchanging them.

Algebraic dual

Let G be a connected graph. An algebraic dual of G is a graph G^★ so that G and G^★ have the same set of edges, any cycle of G is a cut of G^★, and any cut of G is a cycle of G^★. Every planar graph has an algebraic dual which is in general not unique (any dual defined by a plane embedding will do). The converse is actually true, as settled by Whitney:^[2]

A connected graph G is planar if and only if it has an algebraic dual.

The same fact can be expressed in the theory of matroids: if M is the graphic matroid of a graph G, then the dual matroid of M is a graphic matroid if and only if G is planar. If G is planar, the dual matroid is the graphic matroid of the dual graph of G.

Weak dual

The weak dual of an embedded planar graph is the subgraph of the dual graph whose vertices correspond to the bounded faces of the primal graph. A planar graph is outerplanar if and only if its weak dual is a forest, and a planar graph is a Halin graph if and only if its weak dual is biconnected and outerplanar. For any embedded planar graph G, let G⁺ be the multigraph formed by adding a single new vertex v in the unbounded face of G, and connecting v to each vertex of the outer face (multiple times, if a vertex appears multiple times on the boundary of the outer face); then, G is the weak dual of the planar dual of G⁺.^[3][4]

Notes

1. ^ Here we consider that graphs may have loops and multiple edges to avoid uncommon considerations
2. ^ Whitney, Hassler (1932), "Non-separable and planar graphs", Transactions of the American Mathematical Society 34: 339–362 .
3. ^ Fleischner, Herbert J.; Geller, D. P.; Harary, Frank (1974), "Outerplanar graphs and weak duals", Journal of the Indian Mathematical Society 38: 215–219, MR0389672 .
4. ^ Sysło, Maciej M.; Proskurowski, Andrzej (1983), "On Halin graphs", Graph Theory: Proceedings of a Conference held in Lagów, Poland, February 10–13, 1981, Lecture Notes in Mathematics, 1018, Springer-Verlag, pp. 248–256, doi:10.1007/BFb0071635 .

External links

• Weisstein, Eric W., "Dual graph" from MathWorld.
• Weisstein, Eric W., "Self-dual graph" from MathWorld.