Tree (graph theory)

Trees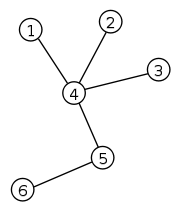
A labeled tree with 6 vertices and 5 edges
Vertices	v
Edges	v - 1
Chromatic number	2 if v > 1
v · mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree. A forest is a disjoint union of trees. The various kinds of data structures referred to as trees in computer science are similar to trees in graph theory, except that computer science trees have directed edges. Although they do not meet the definition given here, these graphs are referred to in graph theory as ordered directed trees (see below). Definitions A tree is an undirected simple graph G that satisfies any of the following equivalent conditions: G is connected and has no cycles. G has no cycles, and a simple cycle is formed if any edge is added to G. G is connected, but is not connected if any single edge is removed from G. G is connected and the 3-vertex complete graph K3 is not a minor of G. Any two vertices in G can be connected by a unique simple path. If G has finitely many vertices, say n of them, then the above statements are also equivalent to any of the following conditions: G is connected and has n − 1 edges. G has no simple cycles and has n − 1 edges. An irreducible (or series-reduced) tree is a tree in which there is no vertex of degree 2. A forest is an undirected graph, all of whose connected components are trees; in other words, the graph consists of a disjoint union of trees. Equivalently, a forest is an undirected cycle-free graph. As special cases, an empty graph, a single tree, and the discrete graph on a set of vertices (that is, the graph with these vertices that has no edges), all are examples of forests. The term hedge sometimes refers to an ordered sequence of trees. A polytree or oriented tree is a directed graph with at most one undirected path between any two vertices. In other words, a polytree is a directed acyclic graph for which there are no undirected cycles either. A directed tree is a directed graph which would be a tree if the directions on the edges were ignored. Some authors restrict the phrase to the case where the edges are all directed towards a particular vertex, or all directed away from a particular vertex (see arborescence). A tree is called a rooted tree if one vertex has been designated the root, in which case the edges have a natural orientation, towards or away from the root. The tree-order is the partial ordering on the vertices of a tree with u ≤ v if and only if the unique path from the root to v passes through u. A rooted tree which is a subgraph of some graph G is a normal tree if the ends of every edge in G are comparable in this tree-order whenever those ends are vertices of the tree (Diestel 2005, p. 15). Rooted trees, often with additional structure such as ordering of the neighbors at each vertex, are a key data structure in computer science; see tree data structure. In a context where trees are supposed to have a root, a tree without any designated root is called a free tree. In a rooted tree, the parent of a vertex is the vertex connected to it on the path to the root; every vertex except the root has a unique parent. A child of a vertex v is a vertex of which v is the parent. A leaf is a vertex without children. A labeled tree is a tree in which each vertex is given a unique label. The vertices of a labeled tree on n vertices are typically given the labels 1, 2, …, n. A recursive tree is a labeled rooted tree where the vertex labels respect the tree order (i.e., if u < v for two vertices u and v, then the label of u is smaller than the label of v). An ordered tree or plane tree is a rooted tree for which an ordering is specified for the children of each vertex. An n-ary tree is a rooted tree for which each vertex which is not a leaf has at most n children. 2-ary trees are sometimes called binary trees, while 3-ary trees are sometimes called ternary trees. A terminal vertex of a tree is a vertex of degree 1. In a rooted tree, the leaves are all terminal vertices; additionally, the root, if not a leaf itself, is a terminal vertex if it has precisely one child. Example The example tree shown to the right has 6 vertices and 6 − 1 = 5 edges. The unique simple path connecting the vertices 2 and 6 is 2-4-5-6. Facts Every tree is a bipartite graph and a median graph. Every tree with only countably many vertices is a planar graph. Every connected graph G admits a spanning tree, which is a tree that contains every vertex of G and whose edges are edges of G. Every connected graph with only countably many vertices admits a normal spanning tree (Diestel 2005, Prop. 8.2.4). There exist connected graphs with uncountably many vertices which do not admit a normal spanning tree (Diestel 2005, Prop. 8.5.2). Every finite tree with n vertices, with n > 1, has at least two terminal vertices (leaves). This minimal number of terminal vertices is characteristic of path graphs; the maximal number, n − 1, is attained by star graphs. For any three vertices in a tree, the three paths between them have exactly one vertex in common. Enumeration Given n labeled vertices, there are nn−2 different ways to connect them to make a tree. This result is called Cayley's formula. It can be proven by first showing that the number of trees with vertices 1,2,...,n, of degrees d1,d2,...,dn respectively, is the multinomial coefficient ${n-2 \choose d_1-1, d_2-1, \ldots, d_n-1}.$ An alternative proof uses Prüfer sequences. This is the special case for complete graphs of a more general problem, counting the number of spanning trees in an undirected graph, which can be achieved by computing a determinant according to the matrix tree theorem. The similar problem of counting all the subtrees regardless of size has been shown to be #P-complete in the general case (Jerrum (1994)). Counting the number of unlabeled free trees is a harder problem. No closed formula for the number t(n) of trees with n vertices up to graph isomorphism is known. The first few values of t(n) are 1, 1, 1, 1, 2, 3, 6, 11, 23, 47, 106, 235, 551, 1301, 3159, ... (sequence A000055 in OEIS). Otter (1948) proved the asymptotic estimate: ${t(n) \sim C \alpha^n n^{-5/2} \quad\text{as } n\to\infty,}$ with C = 0.534949606… and α = 2.99557658565…. (Here, f∼g means that $\lim_{n \to \infty} f/g = 1$.) This is a consequence of his asymptotic estimate for the number r(n) of unlabeled rooted trees with n vertices: $r(n) \sim D\alpha^n n^{-3/2} \quad\text{as } n\to\infty,$ with D = 0.43992401257… and α the same as above (cf. Knuth (1997), Chap. 2.3.4.4 and Flajolet & Sedgewick (2009), Chap. VII.5). Types of trees A star graph is a tree which either has order n ≤ 2, or consists of a single internal node (and n − 1 leaves). In other words, a star graph of order n is a tree of order n with as many leaves as possible. Its diameter is at most 2. A tree with two terminal vertices (the fewest possible) is a path graph. If all nodes in a tree are within distance one of a central path subgraph, then the tree is a caterpillar tree. If all nodes are within distance two of a central path subgraph, then the tree is a lobster. See also Decision tree Pseudoforest Tree structure Tree data structure Unrooted binary tree References Diestel, Reinhard (2005), Graph Theory (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-26183-4, http://diestel-graph-theory.com/index.html . Flajolet, Philippe; Sedgewick, Robert (2009), Analytic Combinatorics, Cambridge University Press, ISBN 9780521898065  Donald E. Knuth. The Art of Computer Programming Volume 1: Fundamental Algorithms. Addison-Wesley Professional; 3rd edition (November 14, 1997). Jerrum, Mark (1994), "Counting trees in a graph is #P-complete", Information Processing Letters 51 (3): 111–116, doi:10.1016/0020-0190(94)00085-9, ISSN 0020-0190 . Otter, Richard (1948), "The Number of Trees", Annals of Mathematics, Second Series 49 (3): 583–599, doi:10.2307/1969046, JSTOR 1969046 . Wikimedia Foundation. 2010. Игры ⚽ Поможем решить контрольную работу Synagogue Air traffic control Look at other dictionaries: Tree (set theory) — In set theory, a tree is a partially ordered set (poset) ( T …   Wikipedia Graph theory — In mathematics and computer science, graph theory is the study of graphs : mathematical structures used to model pairwise relations between objects from a certain collection. A graph in this context refers to a collection of vertices or nodes and …   Wikipedia Dominator (graph theory) — For Dominating set problem, see Dominating set. In computer science, in control flow graphs, a node d dominates a node n if every path from the start node to n must go through d. Notationally, this is written as d dom n (or sometimes d n). By… …   Wikipedia Star (graph theory) — Star The star S7. (Some authors index this as S8.) Vertices k+1 Edges k …   Wikipedia Bridge (graph theory) — A graph with 6 bridges (highlighted in red) An undirected connected graph with no cut …   Wikipedia Geometric graph theory — In mathematics, a geometric graph is a graph in which the vertices or edges are associated with geometric objects or configurations. Geometric graph theory is a specialization of graph theory that studies geometric graphs. Notable geometric… …   Wikipedia Minor (graph theory) — In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G. The theory of graph minors began with Wagner s theorem that a graph… …   Wikipedia Connectivity (graph theory) — In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements (nodes or edges) which need to be removed to disconnect the remaining nodes from each other[1]. It is… …   Wikipedia Topological graph theory — In mathematics topological graph theory is a branch of graph theory. It studies the embedding of graphs in surfaces, and graphs as topological spaces. [J.L. Gross and T.W. Tucker, Topological graph theory, Wiley Interscience, 1987] Embedding a… …   Wikipedia Degeneracy (graph theory) — In graph theory, a k degenerate graph is an undirected graph in which every subgraph has a vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph s edges. The degeneracy of a graph is the smallest… …   Wikipedia 18+ © Academic, 2000-2024 Contact us: Technical Support, Advertising Dictionaries export, created on PHP, Joomla, Drupal, WordPress, MODx. Mark and share Search through all dictionaries Translate… Search Internet Share the article and excerpts Direct link … Do a right-click on the link above and select “Copy Link”