Star (graph theory)

Star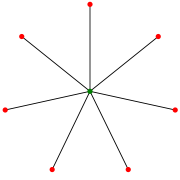
The star S7. (Some authors index this as S8.)
Vertices	k+1
Edges	k
Diameter	minimum of (2, k)
Girth	∞
Chromatic number	minimum of (2, k + 1)
Chromatic index	k
Spectral Gap	1
Properties	Edge-transitive Tree Unit distance Bipartite
Notation	Sk
v · graph theory, a star Sk is the complete bipartite graph K1,k: a tree with one internal node and k leaves (but, no internal nodes and k + 1 leaves when k ≤ 1). Alternatively, some authors define Sk to be the tree of order k with maximum diameter 2; in which case a star of k > 2 has k − 1 leaves. A star with 3 edges is called a claw. The star Sk is edge-graceful when k is even and not when k is odd. It is an edge-transitive matchstick graph, and has diameter 2 (when k > 1), girth ∞ (it has no cycles), chromatic index k, and chromatic number 2 (when k > 0). Stars may also be described as the only connected graphs in which at most one vertex has degree greater than one. Relation to other graph families Claws are notable in the definition of claw-free graphs, graphs that do not have any claw as an induced subgraph.[1][2] A star is a special kind of tree. As with any tree, stars may be encoded by a Prüfer sequence; the Prüfer sequence for a star K1,k consists of k − 1 copies of the center vertex.[3] Several graph invariants are defined in terms of stars. Star arboricity is the minimum number of forests that a graph can be partitioned into such that each tree in each forest is a star,[4] and the star chromatic number of a graph is the minimum number of colors needed to color its vertices in such a way that every two color classes together form a subgraph in which all connected components are stars.[5] The graphs of branchwidth 1 are exactly the graphs in which each connected component is a star.[6] The star graphs S3, S4, S5 and S6. Other applications The set of distances between the vertices of a claw provides an example of a finite metric space that cannot be embedded isometrically into a Euclidean space of any dimension.[7] The star network, a computer network modeled after the star graph, is important in distributed computing. References ^ Faudree, Ralph; Flandrin, Evelyne; Ryjáček, Zdeněk (1997), "Claw-free graphs — A survey", Discrete Mathematics 164 (1–3): 87–147, doi:10.1016/S0012-365X(96)00045-3, MR1432221 . ^ Chudnovsky, Maria; Seymour, Paul (2005), "The structure of claw-free graphs", Surveys in combinatorics 2005, London Math. Soc. Lecture Note Ser., 327, Cambridge: Cambridge Univ. Press, pp. 153–171, MR2187738, http://www.columbia.edu/~mc2775/claws_survey.pdf . ^ Gottlieb, J.; Julstrom, B. A.; Rothlauf, F.; Raidl, G. R. (2001), "Prüfer numbers: A poor representation of spanning trees for evolutionary search", Proc. Genetic and Evolutionary Computation Conference, Morgan Kaufmann, pp. 343–350, http://www.ads.tuwien.ac.at/publications/bib/pdf/gottlieb-01.pdf . ^ Hakimi, S. L.; Mitchem, J.; Schmeichel, E. E. (1996), "Star arboricity of graphs", Discrete Math. 149: 93–98, doi:10.1016/0012-365X(94)00313-8  ^ Fertin, Guillaume; Raspaud, André; Reed, Bruce (2004), "Star coloring of graphs", Journal of Graph Theory 47 (3): 163–182, doi:10.1002/jgt.20029 . ^ Robertson, Neil; Seymour, Paul D. (1991), "Graph minors. X. Obstructions to tree-decomposition", Journal of Combinatorial Theory 52 (2): 153–190, doi:10.1016/0095-8956(91)90061-N . ^ Linial, Nathan (2002), "Finite metric spaces–combinatorics, geometry and algorithms", Proc. International Congress of Mathematicians, Beijing, 3, pp. 573–586, arXiv:math/0304466  Wikimedia Foundation. 2010. Игры ⚽ Поможем написать реферат Aptera Typ-1 Anton Strout Look at other dictionaries: Tree (graph theory) — Trees A labeled tree with 6 vertices and 5 edges Vertices v Edges v 1 Chromatic number …   Wikipedia Vertex (graph theory) — For other uses, see Vertex (disambiguation). A graph with 6 vertices and 7 edges where the vertex number 6 on the far left is a leaf vertex or a pendant vertex In graph theory, a vertex (plural vertices) or node is the fundamental unit out of… …   Wikipedia Snark (graph theory) — In graph theory, a snark is a connected, bridgeless cubic graph with chromatic index equal to 4. In other words, it is a graph in which every vertex has three neighbors, and the edges cannot be colored by three colors without two edges of the… …   Wikipedia Glossary of graph theory — Graph theory is a growing area in mathematical research, and has a large specialized vocabulary. Some authors use the same word with different meanings. Some authors use different words to mean the same thing. This page attempts to keep up with… …   Wikipedia List of graph theory topics — This is a list of graph theory topics, by Wikipedia page. See glossary of graph theory for basic terminology Contents 1 Examples and types of graphs 2 Graph coloring 3 Paths and cycles 4 …   Wikipedia Star (disambiguation) — A star is a luminous cosmic body. For uses of stars as a symbol, see List of symbolic stars.Star or stars may also refer to:Places*Star Mountains, a mountain range in Papua New GuineaUnited Kingdom*Star, Anglesey, Wales *Star, Fife, Scotland… …   Wikipedia Graph coloring — A proper vertex coloring of the Petersen graph with 3 colors, the minimum number possible. In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called colors to elements of a graph… …   Wikipedia Star network — Star networks are one of the most common computer network topologies. In its simplest form, a star network consists of one central switch, hub or computer, which acts as a conduit to transmit messages. Thus, the hub and leaf nodes, and the… …   Wikipedia star — starless, adj. /stahr/, n., adj., v., starred, starring. n. 1. any of the heavenly bodies, except the moon, appearing as fixed luminous points in the sky at night. 2. Astron. any of the large, self luminous, heavenly bodies, as the sun, Polaris,… …   Universalium Petersen graph — Infobox graph name = Petersen graph image caption = The Petersen graph is most commonly drawn as a pentagon with a pentagram inside, with five spokes. namesake = Julius Petersen vertices = 10 edges = 15 radius = 2 diameter = 2 girth = 5 chromatic …   Wikipedia 18+ © Academic, 2000-2024 Contact us: Technical Support, Advertising Dictionaries export, created on PHP, Joomla, Drupal, WordPress, MODx. Mark and share Search through all dictionaries Translate… Search Internet Share the article and excerpts Direct link … Do a right-click on the link above and select “Copy Link”