- Degree (graph theory)
-
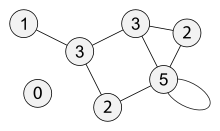
In graph theory, the degree (or valency) of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice.[1] The degree of a vertex v is denoted deg(v). The maximum degree of a graph G, denoted by Δ(G), and the minimum degree of a graph, denoted by δ(G), are the maximum and minimum degree of its vertices. In the graph on the right, the maximum degree is 5 and the minimum degree is 0. In a regular graph, all degrees are the same, and so we can speak of the degree of the graph.
Contents
Handshaking lemma
Main article: handshaking lemmaThe degree sum formula states that, given a graph G = (V,E),
The formula implies that in any graph, the number of vertices with odd degree is even. This statement (as well as the degree sum formula) is known as the handshaking lemma. The latter name comes from a popular mathematical problem, to prove that in any group of people the number of people who have shaken hands with an odd number of other people from the group is even.
Degree sequence
The degree sequence of an undirected graph is the non-increasing sequence of its vertex degrees;[2] for the above graph it is (5, 3, 3, 2, 2, 1, 0). The degree sequence is a graph invariant so isomorphic graphs have the same degree sequence. However, the degree sequence does not, in general, uniquely identify a graph; in some cases, non-isomorphic graphs have the same degree sequence.
The degree sequence problem is the problem of finding some or all graphs with the degree sequence being a given non-increasing sequence of positive integers. (Trailing zeroes may be ignored since they are trivially realized by adding an appropriate number of isolated vertices to the graph.) A sequence which is the degree sequence of some graph, i.e. for which the degree sequence problem has a solution, is called a graphic or graphical sequence.
The problem of finding or estimating the number of graphs with a given degree sequence is a problem from the field of graph enumeration.
As a consequence of the degree sum formula, any sequence with an odd sum, such as (3, 3, 1), cannot be realized as the degree sequence of a graph. The converse is also true: if a sequence has an even sum, it is the degree sequence of a graph. The construction of such a graph is simple: connect odd vertices in pairs, and fill with self-loops.
Often one wishes to search for simple graphs, making the degree sequence problem more challenging. Obviously the sequence (8, 4) is not the degree sequence of a simple graph, since we would have the contradiction Δ(G) > (number of vertices − 1). The sequence (3, 3, 3, 1) is also not the degree sequence of a simple graph, but in this case the reason is less obvious. Finding general criteria for degree sequences of simple graphs is a classical problem; solutions have been offered by Erdős and Gallai (1960), V. J. Havel (1955) and S. L. Hakimi (1961), S. A. Choudum and Sierksma et al. (1991).
For example, the Erdős–Gallai theorem states that a non-increasing sequence of n numbers di (for i = 1,...,n) is the degree sequence of a simple graph if and only if the sum of the sequence is even and
Havel and Hakimi proved that (d1, d2, ..., dn) is a degree sequence of a simple graph if and only if (d2 − 1, d3 − 1, ..., dd1+1 − 1, dd1+2, dd1+3, ..., dn) is. This fact leads to a simple algorithm (the Havel-Hakimi algorithm) for realizing a simple graph with a given realizable degree sequence: Begin with a graph with no edges. Maintain a list of vertices whose degree requirement has not yet been met in non-increasing order of residual degree requirement. Connect the first vertex to the next d1 vertices in this list, and then remove it from the list. Re-sort the list and repeat until all degree requirements are met.
Special values
- A vertex with degree 0 is called an isolated vertex.
- A vertex with degree 1 is called a leaf vertex or end vertex, and the edge incident with that vertex is called a pendant edge. In the graph on the right, {3,5} is a pendant edge. This terminology is common in the study of trees in graph theory and especially trees as data structures.
Global properties
- If each vertex of the graph has the same degree k the graph is called a k-regular graph and the graph itself is said to have degree k.
- An undirected, connected graph has an Eulerian path if and only if it has either 0 or 2 vertices of odd degree. If it has 0 vertices of odd degree, the Eulerian path is an Eulerian circuit.
- A directed graph is a pseudoforest if and only if every vertex has outdegree at most 1. A functional graph is a special case of a pseudoforest in which every vertex has outdegree exactly 1.
- By Brooks' theorem, any graph other than a clique or an odd cycle has chromatic number at most Δ, and by Vizing's theorem any graph has chromatic index at most Δ + 1.
- A k-degenerate graph is a graph in which each subgraph has a vertex of degree at most k.
See also
- Indegree, outdegree for digraphs
- Degree distribution
Notes
References
- Diestel, Reinhard (2005), Graph Theory (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-26183-4, http://www.math.uni-hamburg.de/home/diestel/books/graph.theory/.
- G. Sierksma and H. Hoogeveen, "Seven criteria for integer sequences being graphic, " Journal of Graph Theory 15, No. 2 (1991) 223–231.
Categories:
Wikimedia Foundation. 2010.